执行器饱和的不确定时滞系统的镇定

杜鸿波，景 丽

（沈阳师范大学 数学与系统科学学院，沈阳 110034）

0 引 言

饱和现象广泛地存在于各种工业系统当中，对实际工程来说，控制往往属于容许控制，即控制输入需要满足一定的约束条件，执行器饱和限制是一种最常见的约束控制，所以对于这类问题的研究自然就有非常重要的意义。

1964年Fuller首次提出饱和系统，20世纪90年代，学者们对饱和系统的理论研究热情高涨，取得了丰硕的成果。近几年，Hu等［1－2］针对状态反馈下的执行器饱和控制系统，利用饱和非线性的特性，提出了凸组合的处理方法，通过引入辅助矩阵H处理饱和非线性项，将稳定条件转化为线性矩阵不等式，通过LMI求解。司玉琴等［3］研究了多输入线性系统的全局稳定性，通过迭代算法进行吸引域估计。Cao等［4］基于饱和关联函数，给出了线性离散系统的稳定性判据，应用线性矩阵不等式计算最大吸引域。2008年，Zou等［5］通过对Lyapunov方程的模型转换，给出了一种改进的稳定条件。Guan等［6］基于锥互补的线性化程序给出了动态输出反馈控制器的设计方法。2010年，Ma等［7］根据Finsler’s引理，得到了线性离散执行器饱和控制系统稳定性新方法，并通过迭代算法进行吸引域估计。2011年，朱发旺等［8］及基于饱和关联函数研究了线性离散时间系统的吸引域估计问题，通过为每一个椭球寻找辅助的增益矩阵来降低吸引域估计的保守性。针对含有不确定项的执行器饱和问题，魏爱荣等［9］基于饱和度函数，研究了单输入不确定线性系统的稳定性。针对含有时滞的执行器饱和问题，Hind等［10－12］相继应用扇形非线性法进行研究分析，得到了相应的稳定性条件。此外，张美玉等［13－14］将饱和应用到时滞切换系统中，并给出了控制器的设计。

本文根据文献［10］和文献［12］研究含有不确定时滞的执行器饱和问题，给出了使系统渐近稳定的无记忆状态反馈控制器的存在条件和设计方案。

1 问题描述

考虑以下状态方程描述的带有不确定时滞的执行器饱和系统：

其中：x（t）∈Rn为系统状态向量；u（t）∈Rm为控制输入向量；d＞0是滞后的时间常数；φ（t）为初始函数；A、Ad、B为适当维数的实值矩阵；ΔA（t）、ΔAd（t）和ΔB（t）是不确定实值矩阵，且具有范数有界不确定性结构，可写成其中H、E1、Ed、E2是已知实数矩阵，N（t）为元素是Lebesgue可测的不确定矩阵，但是满足不等式NT（t）N（t）≤I；sat（·）表示饱和非线性函数，定义如下：

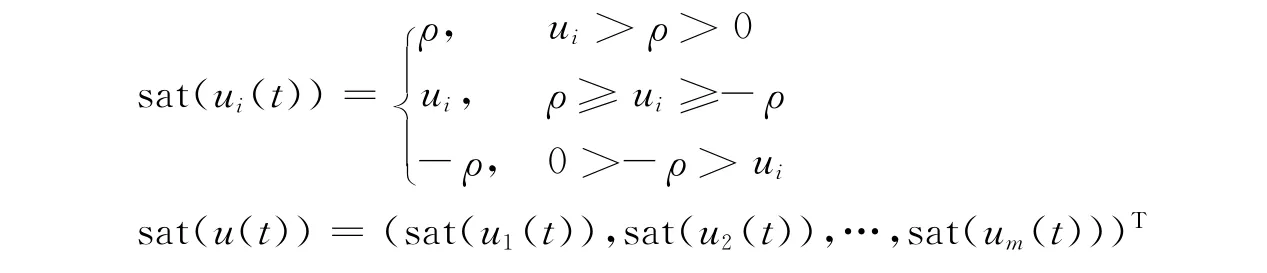
2 稳定性分析

对于执行器饱和系统的研究，早期将饱和函数建模在一个扇形区域内，利用波波夫（Popov）准则和圆判据，对执行器饱和系统进行稳定性分析。其中比较典型的方法是引入无记忆状态反馈控制器［12］

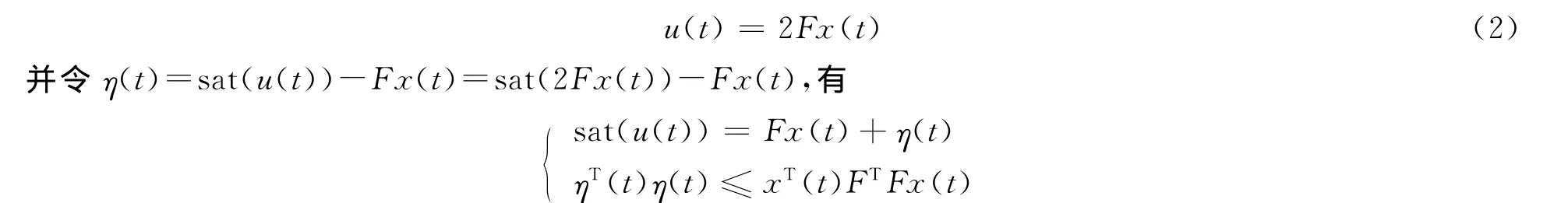
同样，本文对于系统（1）引入无记忆状态反馈（2），则有

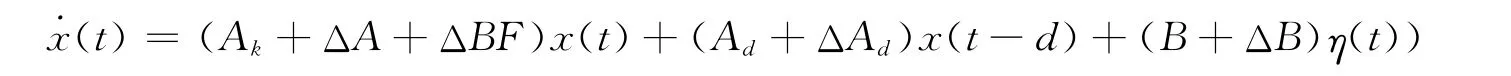
其中Ak＝A＋BF。

定理1 对于闭环系统（1），给定状态反馈控制增益矩阵F，如果存在对称正定矩阵P和S，标量ε＞0，λ＞0，使得下面的矩阵不等式成立：

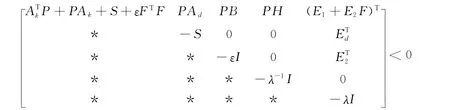
则闭环系统（1）在给定的状态反馈控制器（2）下是渐近稳定的。

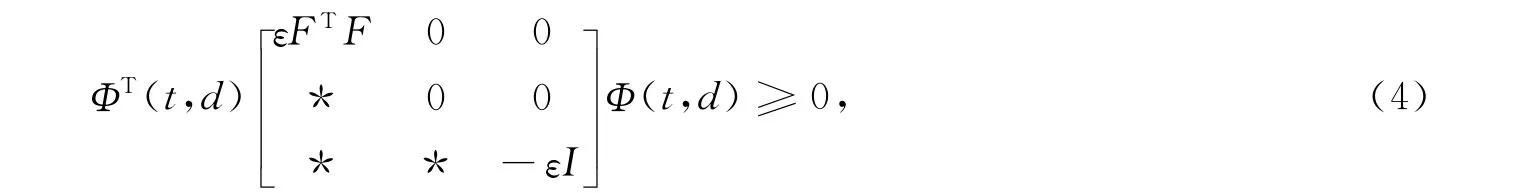
把式（3）与式（4）相加，可知若式（5）成立，则V（t）＜0，

上式对所有满足NT（t）N（t）≤I的参数不确定矩阵N（t）成立，当且仅当存在一个标量λ＞0，使得

根据Schur补引理，可知式（6）等价于

则当式（7）成立时，有V（t）＜0，即闭环系统（1）在给定的状态反馈控制器（2）下是渐近稳定的。

3 控制器设计

定理2 考虑闭环系统（1），如果存在对称正定矩阵P，U和任意适维矩阵Q，标量ε＞0，λ＞0，使得下面的矩阵不等式成立：

则闭环系统（1）在无记忆状态反馈控制器（2）下是渐近稳定的，其中F＝QP－1。

证明 对于（7）式根据Schur补引理可转换为

令＝P－1，Q＝FP－1，U＝P－1SP－1＝ε－1，那么式（10）可写成式（8），则当式（8）成立时，闭环系统（1）在无记忆状态反馈控制器（2）下是渐近稳定的，且状态反馈控制器F＝。

4 仿真算例

例 考虑二阶的控制系统（1），具有如下参数

利用Matlab的LMI工具箱求解矩阵不等式（8），得

选取初始状态x0＝（－2，25）T，则系统的状态轨迹是渐近稳定的，如图1所示。

图1 系统的状态轨迹

5 结 语

本文研究了执行器饱和的不确定时滞系统的镇定问题。基于扇形区域法和李亚普诺夫函数方法研究了闭环系统渐近稳定的条件，并且在系统渐近稳定的条件下，给出了无记忆状态反馈控制器的设计方案，仿真算例验证了结论的有效性和可行性。

［1］HU Tingshu，LIN Zongli，CHEN B M.An analysis and design method for linear systems subject to actuator saturation and disturbance［J］.Automatica，2002，38（2）：351－359.

［2］HU Tingshu，LIN Zongli，CHEN B M.Analysis and design for discrete－time systems subject to actuator saturation［J］.Systems ＆ Control Letters，2002，45（2）：97－112.

［3］司玉琴，陈东彦.具有控制约束的多输入系统全局渐近稳定性［J］.哈尔滨理工大学学报，2009，14（6）：66－69.

［4］CAO Yongyan，LIN Zongli.Stability analysis of discrete－time systems with actuator saturation by a saturationdependent Lyapunov function［J］.Automatica，2003，39（7）：1235－1241.

［5］ZOU Zhiqiang，WANG Yijing.On enlarging the domain of attration for nlinear systems subject to actuator saturation［J］.Int J General Systems，2008，37（2）：239－248.

［6］GUAN Wei，YANG Guanghong.Analysis and design of output feedback control systems with actuator saturation［J］.J Control Theory Appl，2008，6（4）：421－426.

［7］MA Yongmei，YANG Guanghong.Stability analysis for linear discrete－time systems subject to actuator saturation［J］.J Control Theory Appl，2010，8（2）：245－248.

［8］朱发旺，黄腾云，刘和光，等.基于饱和关联Lyapunov函数的饱和离散系统吸引域估计［J］.江南大学学报：自然科学版，2011，10（4）：379－384.

［9］魏爱荣，赵克友.执行器饱和不确定线性系统的分析和设计［J］.电机与控制学报，2006，9（5）：448－451.

［10］HNDI H，BOYD S.Analysis of linear systems with saturation using convex optimization［C］∥Decision and Control，1998.Proceedings of the 37th IEEE Conference on.IEEE，1998：903－908.

［11］张先明，吴敏，佘锦华.含饱和驱动的线性时滞系统的时滞相关鲁棒稳定化［J］.控制理论与应用，2006，22（6）：991－994.

［12］王嘉宁，景丽.具有输入饱和时滞线性系统的渐近稳定性［J］.科技信息，2013，36（457）：69－70.

［13］张美玉，刘玉忠.具有非线性执行器饱和的时滞切换系统的控制器设计［J］.沈阳师范大学学报：自然科学版，2009，27（2）：144－147.

［14］王茂，樊友高，邱剑彬.饱和不确定离散切换系统的静态输出反馈控制［J］.控制与决策，2010，25（10）：1480－1483.

［15］俞立.鲁棒控制线性矩阵不等式处理方法［M］.北京：清华大学出版社，2002.