罕遇地震作用下边坡的动力响应和稳定性分析

关金龙

(中国昆仑工程公司，北京100037)

由于天然边坡富含地下水，尤其是降雨后地下水位升高，甚至会发生饱和，研究考虑地下水时边坡的地震动力响应和稳定性更符合实际。根据《GB 50111—2006 铁路工程抗震设计规范》，铁路工程应按多遇地震、设计地震和罕遇地震3个地震动水准进行抗震分析。且在多遇地震作用下结构的抗震设计可采用反应谱法或者选用合适的地震波采用时程分析法进行，罕遇地震作用下应采用非线性时程反应分析法进行计算。

国内外针对地震作用下边坡的地震动力响应和稳定性作了很多研究。Hatzor［1］研究了动力载荷对边坡稳定性的影响。Griffith［2］和 Lane［3］基于自己开发的有限元软件，利用强度折减法分析了水位变化对边坡安全系数的影响。宋健等［4］研究了具有向前方向性效应、滑冲效应和无速度脉冲的近断层地震动作用下边坡的动力响应。柴红保等［5］对竖直向剪切波作用下边坡的动力响应进行数值模拟。毕忠伟等［6］分析了土质边坡在地震作用下的动力响应规律。言志信等［7］研究了地震作用下边坡的动力响应规律。然而国内外研究多数没有考虑地下水的影响，地下水作为土质边坡的决定影响因素，不容忽视。基于此，本研究开展了考虑地下水影响的砂土边坡的数值仿真分析，研究罕遇地震作用下地下水的存在对边坡地震动力响应和稳定性的影响规律。

1 边坡的数值仿真分析

1.1 仿真模型的建立

本研究计算模型取边坡高度的5倍范围。坡脚前缘岩体宽度取25 m，坡脚后缘宽度取45 m，模型高度取24 m。模型底部假定为固定边界，左右边界假定为滑移边界，且使有限元分析模型网格的最大尺寸小于输入地震波最短波长的1/10～1/8。边坡的物理参数如表1所示。

表1 边坡的物理参数Table 1 Physical parameters of sandy slope

动孔压本构模型采用 Martin、Finn和 Seed(1974，1975)模型，土的本构模型采用摩尔库伦本构模型。地下水位通过改变边坡左侧的水位高度来控制，边坡右侧水位始终控制再坡脚位置，先进行渗流分析，水位稳定后，以其作为动力分析的初始状态，从而通过动孔隙水压力模型可以考虑地震和地下水的耦合。

1.2 地震波的选取

查阅《GB50111—2006 铁路工程抗震设计规范》7.2.2－1多遇地震和罕遇地震的水平地震基本加速度值如表2所示。

表2 水平地震基本加速度值Table 2 Acceleration of horizontal earthquakes

研究的边坡所在地区基本烈度为7度，按照罕遇地震的基本加速度值0.21g进行地震波的调整，分别采用EICentro地震波、远场地震波T1－II－1和近场地震波T2－II－1进行分析，如图1所示。且由于边坡破坏主要受到水平地震的影响，只考虑水平地震的作用。

图1 地震波加速度时程曲线Fig.1 Time history curves of earthquakes wave acceleration

2 基于中日规范的边坡的稳定性分析

拟静力法将地震荷载简化为水平地震力F作用于土条块的质心处。

式中，W为土体重量;Kh为水平地震系数。

当地震加速度峰值在0.2 m/s2以下时:

当地震加速度峰值在0.2 m/s2以上时:

式中，a为地表面水平加速度峰值。

地下水对边坡稳定性的影响考虑为条块单位宽度的动水压力

式中，b为土条块的水平宽度;u为孔隙水压力。

边坡圆弧滑动法原理如图2所示。

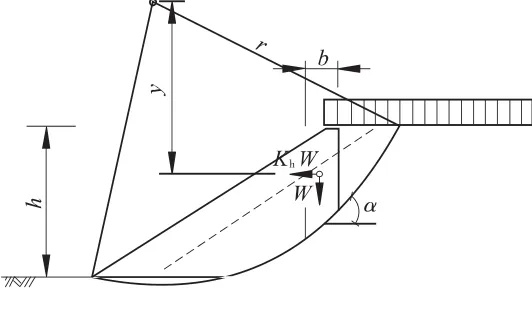
图2 圆弧滑动法示意Fig.2 Schematic diagram of circular sliding method

针对土质边坡，在日本规范中，边坡安全系数

式中，Fs为安全系数;α为斜面切线与水平方向的夹角;为内摩擦角;c为黏聚力;L为圆弧长度;Tr为加固后的抵抗力;r为圆弧半径;y为圆弧中心到条块中心的垂直距离;W为条块重力。

基于中日规范采用拟静力法对边坡进行稳定性分析，计算的边坡安全系数如表3所示。

表3 基于中日规范的边坡安全系数Table 3 Slope safety factors based on the Chinese and Japanese specifications

由表3可知，基于拟静力法对边坡在地下水作用下的安全系数进行求解，可知日本规范计算的结果要比中国规范计算结果偏小，说明在进行边坡稳定性评估时，中国规范的安全系数值相对日本规范较为保守。

3 罕遇地震下边坡的动力响应分析

3.1 边坡动力安全系数分析

进行罕遇地震分析时，中国《GB 50111—2006铁路工程抗震设计规范》指出要采用动力时程法进行分析，基于此本研究针对罕遇地震作用下边坡进行时程分析，求得了边坡的动力安全系数，并与规范中的边坡允许安全系数值进行了对比，如图3～图6所示。

图3 h=3 m时的边坡安全系数Fig.3 Slope safety factor under the water height of 3 m

图4 h=6 m时的边坡安全系数Fig.4 Slope safety factor under the water height of 6 m

由图3～图6可知，随着地下水位的升高边坡的安全系数急剧减小，当水位达到6 m水深时边坡的动力安全系数最小值已经小于规范中的允许值。而达到12 m时，边坡的动力安全系数的最大值已不满足边坡的规定的允许值，说明此时边坡已经发生失稳破坏。

3.2 边坡位移响应分析

研究罕遇地震作用下地下水位3、6、9、12 m时对边坡位移响应的影响，得出其位移如图7所示。

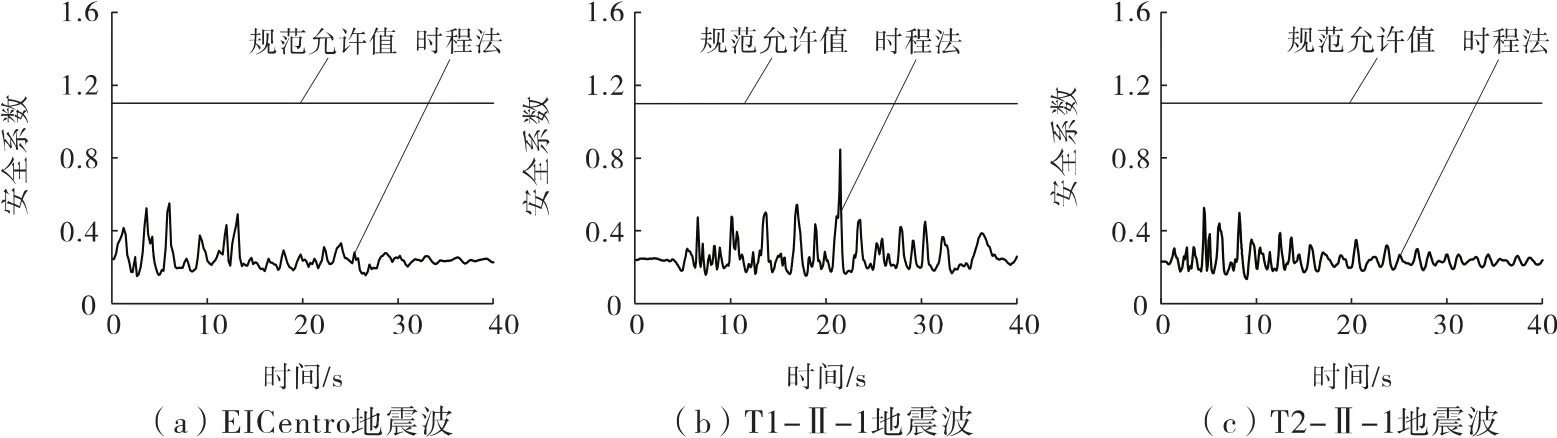
图6 h=12 m时的边坡安全系数Fig.6 Slope safety factor under the water height of 12 m

图7 不同水深下沿边坡高度的最大水平位移Fig.7 The maximum horizontal displacement along the height of the slope under different water depth

由图7可知，在地震作用下，随着h的增加边坡的最大水平位移总体呈现增加的趋势，且在边坡顶部水平位移达到最大值。在h=3 m时，EICentro地震作用下坡顶的最大水平位移为3.36 cm，T1－II－1地震作用下坡顶最大水平位移为4.08 cm，T2－II－1地震作用下坡顶最大水平位移为6.58 cm;在h=6 m时，EICentro地震作用下坡顶的最大水平位移3.56 cm，T1－II－1地震作用下坡顶最大水平位移为3.68 cm，T2－II－1地震作用下坡顶最大水平位移为8.92 cm;在h=9 m时，EICentro地震作用下坡顶的最大水平位移分别为3.72 cm，T1－II－1地震作用下坡顶最大水平位移为7.21 cm，T2－II－1地震作用下坡顶最大水平位移为9.02 cm;在h=12 m时，EICentro地震作用下坡顶的最大水平位移3.02 cm，T1－II－1地震作用下坡顶最大水平位移为8.01 cm，T2－II－1地震作用下坡顶最大水平位移为9.62 cm;由此可知，在不同地震作用下边坡的位移平均值呈现增大的趋势，且边坡在近场地震作用下的位移要大于远场地震作用下的位移。

3.3 边坡加速度响应分析

为了研究地下水位变化对边坡地震动力响应的影响，首先通过定义边坡左侧和右侧总水头的高度，进行边坡的稳定渗流分析，确定出边坡的浸润线位置，将其作为边坡动力分析的初始水位，进行边坡的地震动力响应研究，如图8所示。

由图8可知，在地震作用下，随着水深的增加，边坡的最大水平加速度有减小的趋势。且随着边坡高度的增加均呈现出增大趋势，表现出明显的动力放大效应。在h=3 m时，EICentro地震作用下坡顶的最大水平加速度为3.02 m/s2，T1－II－1地震作用下坡顶最大水平加速度为3.67 m/s2，T2－II－1地震作用下坡顶最大水平加速度为4.32 m/s2;在h=6 m时，EICentro地震作用下坡顶的最大水平加速度为2.96 m/s2，T1－II－1地震作用下坡顶最大水平加速度为3.43 m/s2，T2－II－1地震作用下坡顶最大水平加速度为3.91 m/s2;在h=9 m时，EICentro地震作用下坡顶的最大水平加速度为2.91 m/s2，T1－II－1地震作用下坡顶最大水平加速度为3.48 m/s2，T2－II－1地震作用下坡顶最大水平加速度为4.02 m/s2;在h=12 m时，EICentro地震作用下坡顶的最大水平加速度为2.93 m/s2，T1－II－1地震作用下坡顶最大水平加速度为3.31 m/s2，T2－II－1地震作用下坡顶最大水平加速度为3.78 m/s2;由此可知，在不同地震作用下边坡的最大水平加速度呈现减小的趋势，且边坡在近场地震作用下的加速度要大于远场地震作用下的水平加速度。

图8 不同水深下沿边坡高度的最大水平加速度Fig.8 The maximum horizontal acceleration along the height of the slope under different water depth

3.4 边坡的应力和应变分析

岩体中应力场分布是研究边坡动力响应的重要内容，决定了岩石在加载后是否变形或发生破坏。本研究计算了EICentro地震作用下边坡的剪应力，如图9所示。

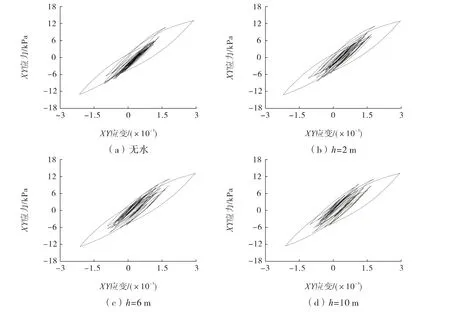
图9 不同水深下边坡的XY方向剪应力－应变图Fig.9 XY shear stress strain map of the slope under different water depth

由图9可知，EICentro地震作用下，边坡无水和有水时边坡坡脚的剪应力－剪应变的差异较大，地下水对对边坡坡脚处的抗剪能力都有较大的影响。从剪应力－剪应变曲线可以看出，与无水时相比，剪应力－剪应变曲线变得更为饱满，说明地下水对边坡坡脚的抗剪能力影响较大，即在地下水作用下更容易发生剪出破坏。且随着水深的增加，地下水对边坡坡脚的剪应力和剪应变影响逐渐增大，直到地下水位达到6 m时，随着水深继续增加，地下水对边坡剪应力和剪应变的影响逐渐减弱。

4 罕遇地震作用下边坡的稳定性分析

为了研究地下水位高度对边坡稳定性的影响，本研究分别计算了无水及h分别为2、6和10 m地下水位时的边坡的动力安全系数和永久位移，并通过安全系数和永久位移对边坡的破坏模式进行了稳定性分析，对EICentro地震作用进行了研究，如图10和图11所示。

图10 不同水位时边坡的破坏模式Fig.10 Failure modes under different water height

图11 不同水位时边坡的安全系数和永久位移Fig.11 Safety factors and the permanent displacements under different water height

由图10和图11可知，在EICentro地震波作用下，地下水的存在对边坡稳定性有较大的影响，随着水位的增加，拟静力计算的边坡的安全系数由无水时的2.366减小到0.193(边坡破坏)，减少了12.26倍。通过动力时程计算的边坡的动力安全系数的最小值均比拟静力计算的安全系数小，说明拟静力计算的安全系数具有一定的局限性。基于New mark方法计算的边坡无水时的永久位移为0，h=2 m时永久位移为1.25 cm，h=6 m时永久位移为3.86 cm，h=10 m时永久位移呈现无限增大的趋势，说明此时边坡已经发生了滑坡。且在地震作用下，无水时，边坡的破坏主要呈现出通过坡脚的圆弧形剪出破坏。而由于地下水的存在边坡的破坏并没有通过坡脚，而是从边坡前缘某一点处发生了剪出破坏。

5 结论

(1)在进行边坡稳定性评估时，拟静力法计算的中国规范的安全系数值相对日本规范较为保守。

(2)随着地下水位的增加边坡的最大水平位移均表现出增加趋势。沿着边坡高度方向边坡最大水平位移也呈现出增加的趋势，且在坡顶部达到最大值。

(3)有地下水时沿着边坡高度方向的加速度小于无地下水时边坡的加速度，说明地下水的存在一定程度上具有减震作用。此外，由于边坡土体本身对地震动具有放大作用，不同水深时沿着边坡高度方向边坡的最大水平加速度均呈现出增大趋势。

(4)随着水位的增加，地下水对边坡坡脚的剪应力和剪应变影响逐渐增大，直到地下水位达到6 m时，随着水位继续增加，地下水对边坡剪应力和剪应变的影响逐渐减弱。且在地下水作用下更容易发生剪出破坏。

(5)地下水的存在对边坡的稳定性有较大影响，最大水位10 m时，通过拟静力计算的边坡的安全系数比无水时减小了12.26倍。不考虑地下水时，边坡的破坏主要表现为通过坡脚的圆弧形剪出破坏，而地下水的存在使边坡的破坏并没有通过坡脚，而是从边坡前缘某一点处发生剪出破坏。

［1］ Hatzor Y H，Arzib A A，Zaslavskyc Y，et al.Dynamic stability analysis of jointed rock slopes using the DDA method［J］.International Journal of Rock Mechanics ＆ Mining Sciences，2004，41:813-832.

［2］ Griffiths D V，Lane P A.Slopes stability analysis by finite elements［J］.Geotechnique，1999，49(3):387-403.

［3］ Lane P A，Griffiths D V.Assessment of stability of slopes under drawdown conditions［J］.Journal of Geotechnical and Geo-environmental Engineering，2000，126(5):443-450.

［4］ 宋 健，高广运，陈青生，等.近断层地震动作用下土质边坡动力响应研究［J］. 地震工程学报，2013，35(1):63-68.Song Jian，Gao Guangyun，Chen Qingsheng，et al.Dynamic response of soil slope under near-fault ground motions［J］.China Earthquakes Engineering Journal，2013，35(1):63-68.

［5］ 柴红保，曹 平，林 杭.竖直向上传播剪切波作用下边坡动力响应规律［J］. 中南大学学报，2011，42(4):1080-1084.Chai Hongbao，Cao Ping，Lin Hang.Dynamic response laws of slope under vertical shear wave［J］.Journal of Central South University，2011，42(4):1080-1084.

［6］ 毕忠伟，张 明，金 峰，等.地震作用下边坡的动态响应规律研究［J］. 岩土力学，2009，30(S):180-183.Bi Zhongwei，Zhang Ming，Jin Feng，et al.Dynamic response of slopes under earthquakes［J］.Rock and Soil Mechanics，2009，30(S):180-183.

［7］ 言志信，郭 斌，张学东，等.黄土边坡动力响应分析［J］.防灾减灾工程学报，2012，32(5):630-634.Yan Zhixin，Guo Bin，Zhang Xuedong，et al.Dynamic response analysis of loess slope［J］.Journal of Disaster Prevention and Mitigation Engineering，2012，32(5):630-634.