颗粒堆积型多孔介质非线性渗流的试验研究
刘 杰 徐曾和 闫虎城 宫丽丽
(东北大学资源与土木工程学院,辽宁沈阳110819)
多孔介质体的渗流问题涉及到水文地质工程、环境工程、石油工程以及采矿工程等诸多领域[1-3],是构成众多工程问题的基本过程。流体在多孔介质中的流动是复杂的相互耦合效应过程。目前在所进行的流固耦合研究中,一般假设影响渗流场主要参数之一的渗透系数为常量。然而,工程中所涉及到的土壤、岩石及人造多孔介质体均为可变形体,当多孔介质在应力作用下变形时,孔隙结构也同时改变,从而影响到其渗透特性。
自Biot[4]提出了有效应力与渗流场之间关系以来,国内外学者广泛开展了岩石渗流规律演化的研究,Louis[5]通过试验发现渗透系数随正应力的增大而减小,二者之间呈负指数关系。彭苏萍等[6]通过试验分析了砂岩在全应力-应变过程中渗透率的变化规律和不同围压下的孔渗性,建立了砂岩应力-应变与渗透率之间的定性定量关系。黄远智等[7]进行了砂岩渗透试验,通过定义渗透率对有效应力的敏感系数建立了岩样渗透率与有效应力的函数关系式。由此可知,渗透率取决于有效应力与孔隙压力,然而,不同学者所采用的试验仪器及方法各有不同,结论也具有很大的差异性,迄今为止仍未形成一个大家公认的岩体渗透率与应力的函数关系式。
近年来,以岩石介质为对象开展非线性渗流研究较多[5-7]。而对颗粒孔隙较大的人造多孔介质体如充填体的研究则很少。鉴于此,本研究对颗粒堆积型多孔介质体开展了恒轴压与恒围压不同孔隙压力条件下的渗流试验研究。
1 试验材料及方法
1.1 试样制备
利用40~50目与120~140目的白刚玉做骨架材料,选用环氧树脂作为黏结剂。试样制作过程是将配置好的刚玉,加入环氧树脂,放入圆柱体模具中,通过压力机压制形成孔隙分布均匀的试样。试样尺寸规格为12 mm×65 mm,选取其中一个试样进行渗透试验,利用NAP-1型自动孔隙度仪测得孔隙率为28%,力学试验测得试样单轴抗压强度为20 MPa,可以保证渗流试验过程中试样在弹性范围内发生变形。
1.2 试验方法
采用SLB-1型应力应变式三轴剪切渗透试验仪对试样进行恒水头渗流试验。试验原理如图1所示,图中σ1为围压,σ0为轴压,PL为试样上端水压,P0为试样底端水压。在试样的两端各放一块多孔板,目的是使水压能均匀的施加于试样两端面,多孔板中心各有一个竖向小孔,为水流通道。利用孔隙压力系统在两端施加压力PL=P0,然后释放上部孔隙压力连通大气压,使孔隙压力差ΔP=P0。采用电子天平量测渗水量进而换算出相应时间段内的渗流量。取制备的完全饱和试样,进行不同围压与轴压下的4组试验,每组试验中围压与轴压控制不变,底部孔隙压力分别设定为10,20,…,70 kPa,试验方案如表1所示。

图1 试验原理Fig.1 Testing principle

表1 试验方案Table 1 Testing program kPa
2 可变渗透系数的试验原理
传统渗透系数的测定主要是依据Darcy定律
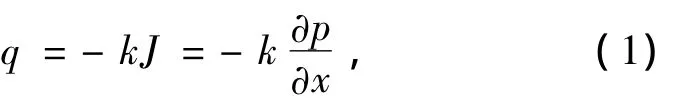
式中,q为渗流速度;假定孔隙压力梯度均匀,即

L为试样长度。按照经典渗流力学计算得到的渗透系数为常量。但是在油气开采,瓦斯开采等工程问题中,渗流实质上是偏离Darcy定律的非线性问题。通常,当渗透系数变化较大时,可以用指数函数拟合渗透系数与孔隙压力或介质应力的关系[6]。本研究考虑到由于荷载作用,高孔隙率下颗粒堆积型多孔介质变形情况下的渗流特性,假定渗透系数的变化满足对数关系,即

式中,k0为初始孔隙率;a为度量孔隙压力变化对孔隙率改变的贡献;b为度量总应力变化对孔隙率改变的贡献;p为孔隙压力;σ为总应力,σ =σ0+2σ1;n为多孔介质瞬时孔隙率。
当流体可压缩时,流体质量守恒方程为

对于本次试验,试样被流体饱和,同时其侧面用不透水胶套包裹,因此可看做非线性一维稳定渗流问题,由于σ为常量,结合式(2)与(3)可得质量守恒方程为

试样底部孔隙压力为P0,顶部孔隙压力为PL。则其边界条件为
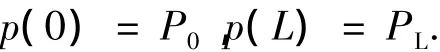
由此解得

设横截面积为S,则从底部流入试样的流量为


从顶部流出试样的流量为

由此可知Q(0)=Q(L),符合流体质量守恒定律。
对于本次试验,考虑到渗流过程中渗透系数具有可变性,同时假设在一维稳定渗流情况下试件内孔隙压力梯度是均匀的,即

则

显然Q(0)≠Q(L),违反流体质量守恒定律。这表明在可变渗透系数的情况下,即使为稳定渗流,试样内孔隙压力梯度均匀的假设仍不成立。
3 试验结果分析与讨论
3.1 渗流的非线性特征
流体流出体积与时间关系曲线受篇幅限制,仅给出底部孔隙压力为70 kPa时第1组与第2组试验结果,如图2所示,渗流过程分为非稳定及稳定渗流2个阶段,稳定段和非稳定段的分界点为稳定渗流临界点,稳定渗流阶段,流体体积与时间呈线性关系。

图2 流体体积与时间的关系Fig.2 Relationship between fluid volume and time
由4组试验中的数据得到渗流速度与孔隙压力梯度的关系如图3所示,渗透系数随着轴压和围压的减小由非线性逐渐趋于线性。所以,假定渗透系数是恒量,利用Darcy定律来处理颗粒型多孔介质的渗流问题是值得商榷的。

图3 渗流速度与孔隙压力梯度的关系Fig.3 Relationship between seepage velocity and gradient of pore pressure
3.2 渗透系数的确定
由式(6)可知,若要求解渗透系数的数学模型中的k0,a,b,必须进行3组试验。由于试验过程中不可避免的存在误差,本研究进行4组试验,对试验数据采用最小二乘法进行参数确定。表2为确定渗透系数试验所得的数据。参数确定后(表3),利用渗透系数的非线性数学模型求解得到试验最大渗透系数,即底端渗透系数k和Darcy定律计算的渗透系数kf进行对比如表4所示,k/kf范围为2.35~2.63倍,由此可知应力作用引起了多孔介质体孔隙结构的改变,从而引起渗透特性的变化。

表2 底部孔隙压力与流量之间关系Table 2 Relationship between bottom pore pressure and flow
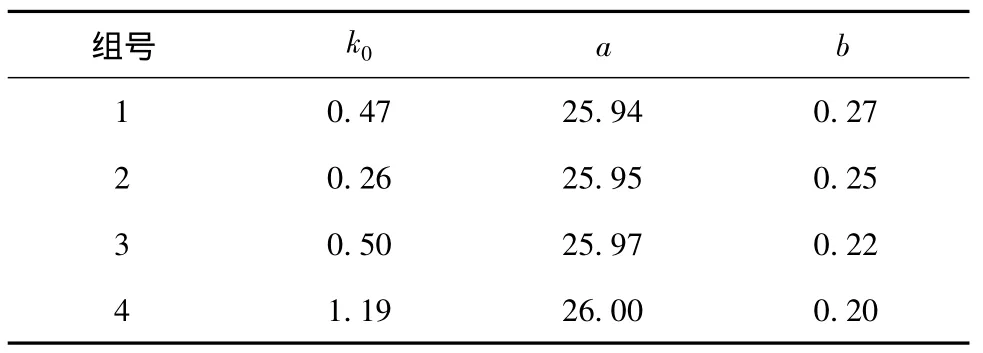
表3 参数计算结果Table 3 Parameter calculation results

表4 渗透系数对比Table 4 Permeability coefficient comparison
4 结论
(1)本研究提出的试验方法可以测试可变形多孔介质体的渗透系数。
(2)提出颗粒堆积型多孔介质体的渗透系数关于应力的指数关系数学模型,并推导了一维稳定渗流问题的理论解答,结果表明在渗透系数可变条件下,试样内孔隙压力梯度具有非均匀性。
(3)渗流过程分为非稳定与稳定渗流阶段;渗透系数随着轴压和围压的减小由非线性逐渐趋于线性。
(4)非线性数学模型与Darcy定律计算得到的渗透系数比值为2.35~2.63,表明由于应力作用而发生的多孔介质体孔隙结构改变不容忽视。
(5)可变形多孔介质渗透系数的数学模型还有对数和幂函数等不同形式,利用各种不同的数学模型研究不同工程背景下的多孔介质体的渗流问题有待进一步研究。
[1] Katsube N,Carroll M M.The modified mixture theory for fluid saturated porous material:theory[J].J Appl Mech,1987,54(3):35-40.
[2] Zienkiewica O C,Shiomi T.Dynamic behavior of saturated porous media:the generalized biot formulation and its numerical solution[J].Int J Num Anal methods Geomech,1984,8(1):237-245.
[3] Lewis R W,Sokirman Y.Finite element molding three phase flow in deformed saturated oil reservoirs[J].Int J Num Anal methods Geomech,1993,17(6):577-598.
[4] Boit M A.General theory of three-dimensional consolidation [J].J Appl Phys,1941,12(2):155-164.
[5] Louis C.Rock Hydraulics in Rock Mechanics[M].New York:Verlay Wien,1974.
[6] 彭苏萍,孟召平,王 虎,等.不同围压下砂岩孔渗规律试验研究[J]. 岩石力学与工程学报,2003,22(5):742-746.Peng Suping,Meng Zhaoping,Wang Hu,et al.Testing study on pore ratio and permeability of sandstone under different confining pressures[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(5):742-746.
[7] 黄远智,王恩志.低渗透岩石渗透率对有效应力敏感系数的试验研究[J]. 岩石力学与工程学报,2007,26(2):742-746.Huang Yuanzhi,Wang Enzhi.Experimental study on coefficient of sensitiveness between percolation rate and effective pressure for low permeability rock [J].Chinese Journal of Rock Mechanics and Engineering,2007,26(2):742-746.

