尾矿物理性质代表参数的研究

曹作忠 张 默 朱君星 江东平

(1.中钢集团马鞍山矿山研究院有限公司，安徽马鞍山243000;2.金属矿山安全与健康国家重点实验室，安徽马鞍山243000;3.金属矿产资源高效循环利用国家工程研究中心，安徽马鞍山243000)

一般来说，表征尾矿的物理性质有多个因素，一个因素有一个或多个指标来体现，如尾矿的孔隙情况可以用孔隙率或孔隙比来表示，指标或因素之间往往又是相互关联的。因此，如能从尾矿众多物理指标中探求决定尾矿堆体稳定性的物理性能本质指标，既可节省人力财力，又可最大限度地减少人为因素和偶然因素对指标精度的影响，本文在研究大量尾矿物理性质试验数据的基础上，利用计算机，采用现代数学中的相关分析与聚类分析法，对尾矿物理性质参数进行分类，从中寻求代表性指标。

1 基础指标选取

通过对国内外尾矿物理性质指标的研究，常用的物理指标可分为物理性质指标和粒级及级配指标，其中物理性质指标包括重力密度、孔隙比、含水量、渗透系数、压实度、固结系数等17个，粒级及级配指标包括平均粒径、不均匀系数等5个。由于尾矿的物理性质指标有基础指标和计算指标，有的基础指标和计算相关性很明显，因此在基础指标选取时删除部分计算指标。另外尾矿的液限、塑限、塑性指数和液限指数是表现尾矿状态的指标，本次研究也将其排除在外。

2 基础指标样本

为了使指标样本具有代表性，本研究在多个铜、铁矿山尾矿试验结果中随机抽取了104个样本［1-2］，样本含有12个基础指标，表1列出了部分参入分析的样本指标。

表1 尾矿物理参数样本Table 1 The sample of tailings physical parameters

3 基础指标的相关性分析

3.1 相关性分析

在统计学中常用相关系数来表示变量之间的相关程度，用相似系数来描述变量之间的相似程度。其原理是假设自变量xi和因变量yi都呈正态分布，则xi和 yi之间的相关系数［3］定义为

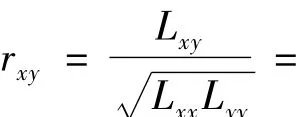
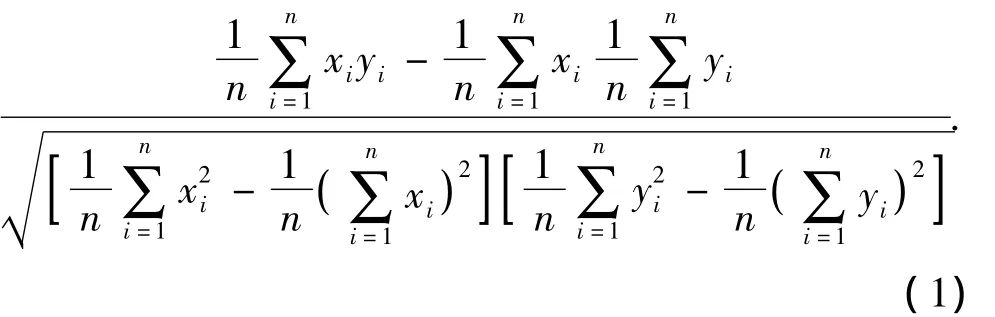
以上相关是单向相关分析，当2个相关变量受到其他各变量影响时，可采用偏相关与单相关分析进行比较，确定其受其他变量的影响。偏相关是用固定其余的变量，消除其余变量的影响，只研究指定两个变量间的纯相关关系，它弥补了简单相关不能真实地反映2个变量间的相关关系。偏相关分为一级偏相关、二级偏相关、……和最高级偏相关，本研究采用最高级偏相关与单相关比较。最高级偏相关是将m－2个变量固定，研究其他2个变量的相关关系。其最高级偏相关系数［4-5］定义为

式中，i，j是1～m个因素中任意2个因素;k是除i，j外的固定因素，有 m － 2 个;cij，k是固定 k 后，i和 j因素的最高级偏相关系数。

按照表1中从左到右的样本参数顺序，12个基础样本参数的平均相关性系数计算结果如下:

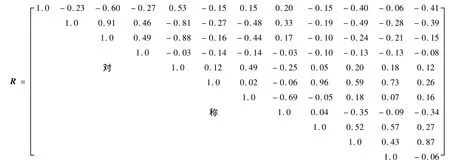
相关系数是相关性大小的度量，其定义域为［－1，1］，一般地:相关系数0.0≤|r|＜0.4为低度相关;相关系数0.4≤|r|＜0.7为中度相关;相关系数0.7≤|r|＜1.0为高度相关。

从相关系数矩阵得出含水量、孔隙比、压缩系数等相关;有效粒径和限制粒径相关;湿密度与干密度、土粒比重相关;渗透系数和固结系数相关;等等。以上相关性通过以下的相关检验，得出相关组。

3.2 相关性检验

一般地，假设样本值、计算值和随机变量x、y母体服从正态分布［2］，则按照下列步骤检验:

(1)当母体相关系数ρ=0，表示随机变量ξ和η之间不相关;ρ≠0，表示随机变量ξ和η之间相关。

(2)选择检验时风险率(也称显著水平)α，本研究选择α=0.01。

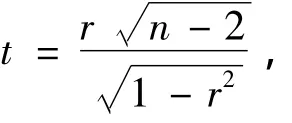
(3)计算统计量此统计服从自由度为(n－2)的t分布。

(4)根据风险率α和统计量t，查t分布表的t临界值ta，本次研究104个样本，ta为2.624，计算临界相关系数

(5)检验相关矩阵，如r≥ra，则2变量与母体显著相关，2变量属于反映事物的同一特征的变量。

各指标之间的相关程度分析见表2所示。

表2 各指标之间的相关程度Table 3 Relative correlation among the index

从检验结果得知:含水量与干密度、孔隙比、限制粒径、不均匀系数中度相关，而与土粒比重低度相关;不均匀系数与限制粒径高度相关，而与含水量中度相关等。按照相关系数的显著性，整个基础指标可以分为3个相关类别，即:第1类，孔隙比、含水量、压缩系数;第2类，压缩模量、土粒比重、干密度、湿密度;第3类，固结系数、渗透系数、不均匀系数、限制粒径、有限粒径。

另外，有些变量为正相关，有的为负相关，在尾矿物理性质分类变量组合时，为避免正负抵消，本研究将采用原始数据倒数的方法对原始数据进行调整后，进行聚类分析。

4 相关组的聚类分析

4.1 聚类分析简介

为使分类合理，必须存在一个描述样品或变量之间亲疏关系的变量，在统计学上一般用“距离”来形象地描述样品或变量之间亲疏关系，“距离”越小表示他们关系越近，“距离”越大则反之。对于单变量很好理解，对于双变量或三变量事物，可以用两维或三维坐标空间2点之间距离描述事物之间的亲疏关系，以次类推，对于m个变量的事物可以看成m维空间的一个点，在点与点之间定义距离。

在统计学上，距离的定义有多种，本研究采用欧氏距离［3-6］。欧氏距离相当于任意m维体的斜边长，简单明了，但它与m个变量的量纲有关，为此，本研究在样品和指标分析时采用以下方法进行调整:

式中，X'ij为标准后的Xij;珔Xij为j(j=1，2，…，m)变量的均值;Xij为第i个样本的j变量;Sj为j变量的标准差;n为样本数目;m为变量数目。

4.2 聚类分析

相关分析给出了各指标之间所存在的联系，但由于其只满足自反性和对称性，而不一定满足传递性，因此在相关的基础上还需对指标进行聚类分析。

在分析时需要输入的是12个变量的相关系数，其系统聚类结果见图1，模糊C均值聚类结果见表3和表4。

图1 基础指标的聚类图Fig.1 The clustering chart of basic indicators

表3 基础指标模糊C均值聚类分析类中心坐标Table 3 The center coordinates for fuzzy C means clustering analysis of the basic index

图1表述的变量系统聚类过程很清楚，指标从各自成类到最后聚集到一类，而表4说明各指标分别聚集到某一类的隶属模大小，某指标在某一类别的隶属模最大，该指标就属于那一类，例如，含水量属于第1、2、3 类的隶属模分别为0.50、0.23、0.27，则含水量属于第1类，以此类推，从而可得到其属类见表5。

表4 基础指标模糊C均值聚类分析隶属模矩阵Table 4 The membership matrix for fuzzy C means clustering analysis of the basic index

表5 基础指标模糊C均值聚类分析结果Table 5 The result of fuzzy C means clustering analysis of the basic index

5 代表指标的选择

为了减少试验，使分析指标简单明了，可在每类指标中选择一个指标作为代表指标，本研究利用(5)式［4］计算每一个指标与同类指标相关系数平均值中最大的作为代表指标，计算结果见表6。

表6 各类指标相关系数平方的平均值Table 6 The average value of correlation coefficient square of all indexes

从表6可以看出，在第1类指标中孔隙比的 值最大，因此孔隙比作为第1类的代表参数，同理，湿密度为第2类代表参数，渗透系数为第3类代表参数，也就是说尾矿的物理性质主要由尾矿的孔隙比、湿密度和渗透系数3个参数决定。

6 结论

(1)通过对尾矿物理性质参数分析，选择了孔隙比、湿密度、渗透系数等12个指标作为尾矿物理性质参数相关分析的基础指标，相关分析表明，基础指标可分为3个相关类别。

(2)在相关的基础上，通过聚类分析，也可将基础指标分为3类，即:第1类:孔隙比、含水量、压缩系数;第2类:压缩模量、土粒比重、干密度、湿密度;第3类:固结系数、渗透系数、不均匀系数、限制粒径、有限粒径。

(3)通过同类指标相关系数平均值分析，得出了决定尾矿物理性质的指标主要是尾矿的孔隙比、湿密度和渗透系数3个参数。

［1］ 张 默，等.某铁尾矿土工织物复合体的真三轴数值试验［J］.金属矿山，2012(11):132-134.Zhang Mo，et al.True triaxial numerical experiment of tailing geotextile compound in an iron mine［J］.Metal Mine，2012(11):132-134.

［2］ 沃廷枢.尾矿库手册［M］.北京:冶金工业出版社，2013.Wo Tingshu.Tailings Handbook［M］.Beijing:Metallurgical Industry Press，2013.

［3］ 浙江大学.概率论与数理统计［M］.北京:高等教育出版社，2002.Zhejiang University.Probability Theory and Mathematical Statistics［M］.Beijing:Higher Education Press，2002.

［4］ John A Rice .Mathematical Statistics and Data Analysis［M］.Belmont，California:Duxbury Press，2007.

［5］ 胡良平.SAS统计分析教程［M］.北京:电子工业出版社，2010.Hu Liangping.Statistical Analysis of SAS Tutorial［M］.Beijing:E-lectronics Industry Publishing House，2010.

［6］ 何正风.MATLAB概率与数理统计分析［M］.北京:机械工业出版社，2012.He Zhengfeng.MATLAB Probability and Mathematical Statistics［M］.Beijing:Mechanical Industry Press，2012.