基于遗传算法的静电微电机优化设计

宫香山，刘晓伟，何广平

(1.北京邮电大学，北京 102613;2.中国航天空气动力技术研究院，北京 100074;3.北方工业大学，北京 100144)

0 引 言

静电微电机是一类具有广泛应用前景的重要MEMS 器件，可用于静电微陀螺［1］、微操作器［2］、微创医疗器械［3］，以及燃料分配、药物精确投放和微流体驱动应用中的微泵［4］。可变电容式静电微电机是最早提出的一类静电微电机［5］，它利用电机定子和转子之间的电容变化来获得输出力矩。这种微电机的缺点是静电力很微小，动态性能十分有限，所以近年来，针对它的优化设计得到了部分学者的关注［6－7］。

本文针对顶面驱动可变电容式静电微电机，提出了一种优化设计方法。这种方法也可用于其他类型的凸极式静电微电机的优化设计。该方法不仅考虑了电机控制方法的优化，还结合了数值积分方法和遗传算法对电机的结构参数进行了优化。试验表明，这种优化设计方法提高了电机的输出力矩，同时大幅减小了输出力矩的波动。

1 顶面驱动静电微电机的数学模型

设顶面驱动可变电容静电微电机的定子和转子都是均布的凸极结构，如图1所示，且电机有np个定子电极，nr个转子凸极。

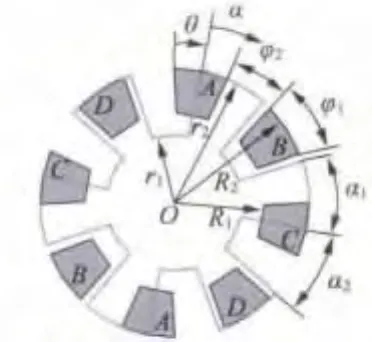
图1 顶面驱动静电微电机的结构原理图

定子电极内缘和外缘半径分别为R1和R2，电极所占角度为φ1，电极间隔角度为φ2。

转子凸极内缘和外缘半径分别为r1和r2，转子凸极所占的角度为α1，转子凸极间的夹角为α2。

基于以上设计，该电机定子相邻两电极之间的相位差:

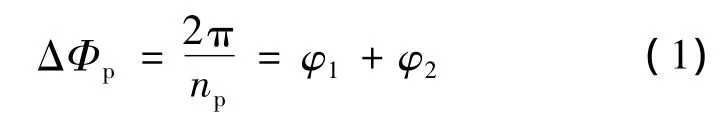
电机转子相邻两凸极之间的相位差:

设定子电极的内径不小于转子凸极的内径，即R1≥r1，且定子电极的外径与转子凸极外径相等，即r2=R2。则转子和定子之间的电容可表示:

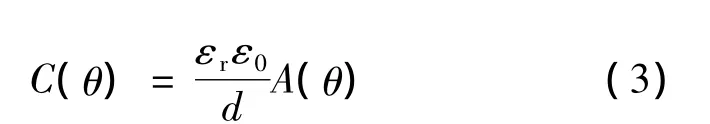
式中:εr为相对介电常数;ε0为真空绝对介电常数，ε0=8.85×10－12F/m;d 为电机转子与定子之间的轴向距离;θ为转子转动的角度;A(θ)为转子凸极与定

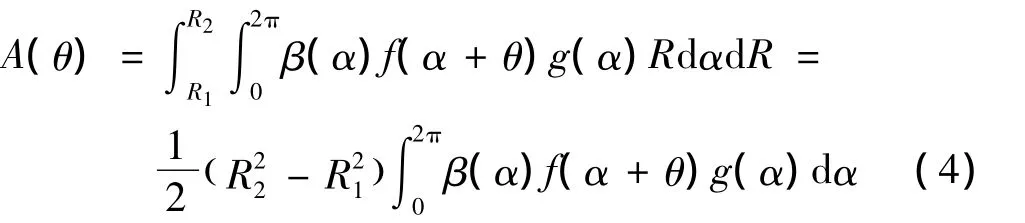
子电极之间的重叠面积。采用极坐标表示方法，A(θ)可表示:式中:α表示转子上任意一点在固联于转子上的极坐标系中的相对角坐标;θ则为转子转动角度在惯性坐标系中的表示，因此α+θ表示转子上任意一点在惯性极坐标系中的角坐标。若定义:

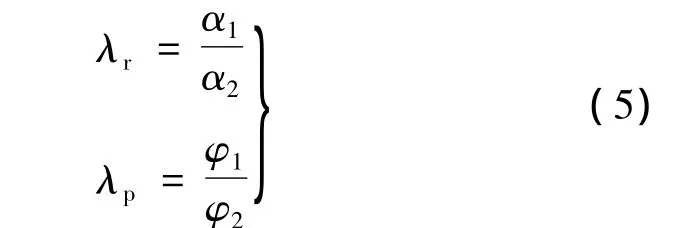
则式(4)中的函数f(α+θ)和g(α)可表示:

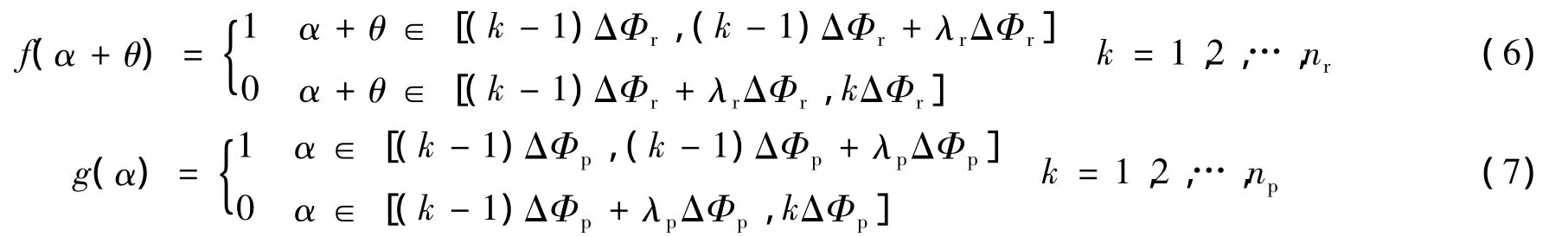
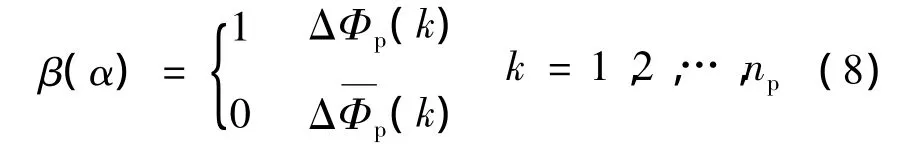
显然，式(6)和式(7)分别表示转子凸极和定子电极沿圆周方向是否存在，当存在于对应区间上时f(α+θ)和g(α)为1，对应区间上不存在转子凸极或定子电极时则为0。而式(8)表示对应定子电极是否施加了非零电压。当施加了非零电压时(用ΔΦp(k)表示)，β(α)为1，否则(用Δ(k)表示)，β(α)为零。考虑电机定子电极和转子凸极分布的均匀性，式(4)还可进一步表示:

静电微电机中存储的电能可表示:

式中:V为通电定子电极上施加的非零电压。利用式(3)和式(10)以及虚功原理，静电电机转子的输出力矩可表示:

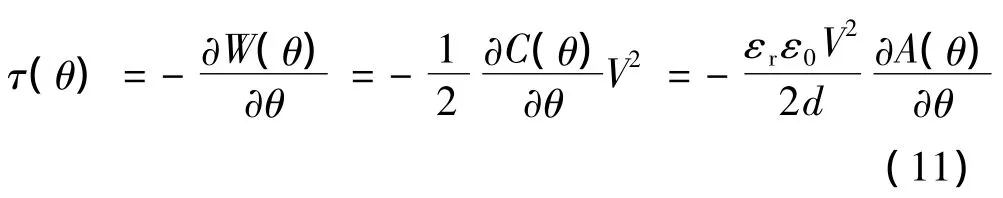
对于顶面驱动静电微电机，由于电机定子和转子形成的平板电容只随两极板间重叠面积A(θ)变化，而A(θ)只是转子位置θ的函数，因此式(11)可表示为常微分形式:

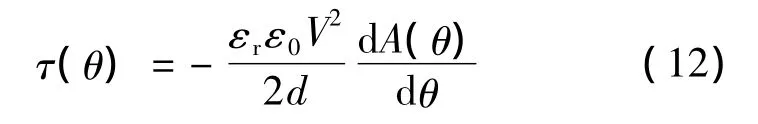
2 顶面驱动静电微电机的驱动方式

当电机采用对称单极控制方式时(这种控制方式的示意图如图2所示)，对于8/6可变电容静电微电机，采用表1所示的电机参数［8］。

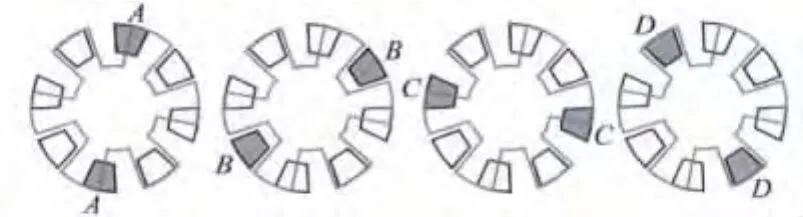
图2 对称单极控制方式

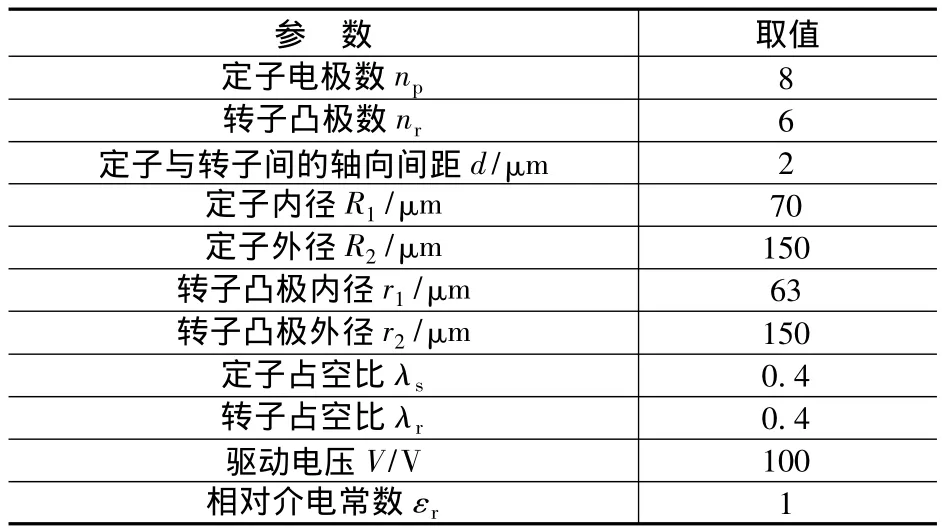
表1 顶面驱动8/6可变电容式静电微电机的物理参数

当不同电极组分别通电时，转子在转动一个凸极位置过程中，转子的输出力矩与转子位置的对应关系如图3所示。通过适当切换通电电极组，可得如图4所示的单向输出扭矩，其平均输出力矩为3.5679×10－10N·m。

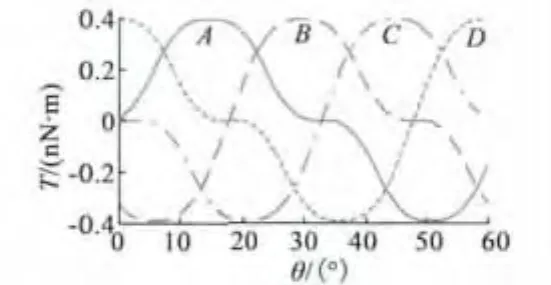
图3 对称单极控制方式下的电机输出力矩

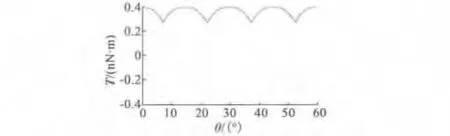
图4 对称单极控制方式下的电机单向最大输出力矩

为了增大电机的输出力矩，本文采用对称相邻双电极并联控制方式(如图5所示)，即在任意时刻只有两对相邻的定子电极通电，转子上可获得的输出扭矩如图6所示。在转子转动过程中，通过切换通电定子电极，且每次只切换第一组电极，则可获得如图7所示的单向最大输出扭矩。在这种控制方式下，输出扭矩的均值为4.5274×10－10N·m，比单极驱动下的平均力矩增大26.89%，但电机输出扭矩的波动较大，这将使电机的负载能力下降。

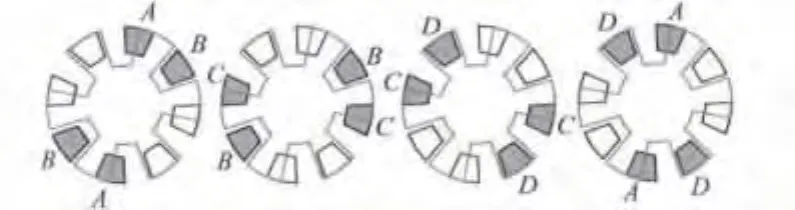
图5 对称相邻双极控制方式

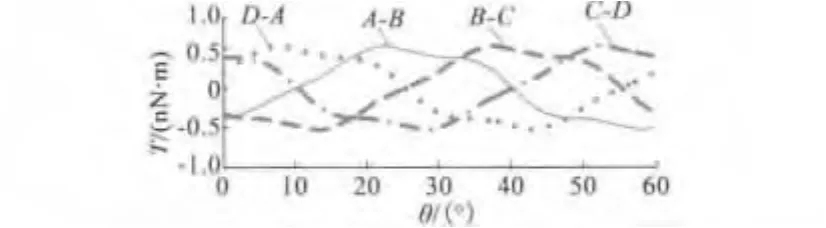
图6 对称相邻双极控制方式下的电机输出力矩

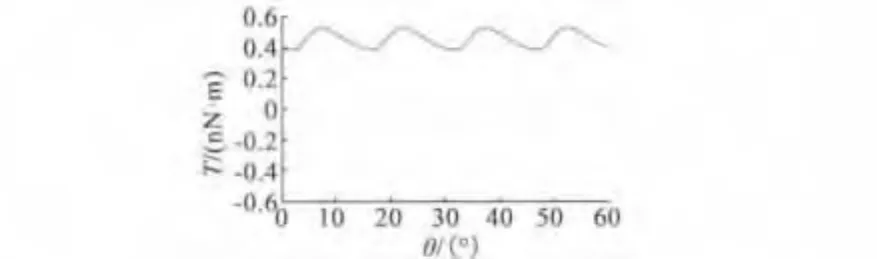
图7 对称相邻双极控制方式下的电机最大输出力矩

3 电机结构参数的优化设计

这里考虑采用优化设计方法改善电机性能，选择优化设计变量:

式中:λs和λr分别为定子电极、转子凸极的占空比。电机的输出力矩均值可表示:

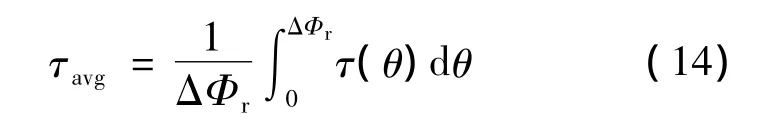
输出力矩的波动系数表示:

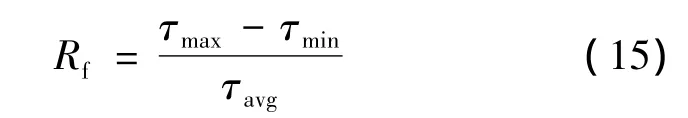
在优化电机的结构参数中，定义三种优化指标，分别:

式中:z1用于优化电机输出力矩;z2用于优化输出力矩波动。式(18)中，λ为加权系数，可以调整z1和z2的数值为同一量级。基于式(16)～式(18)，可建立优化问题的数学模型:

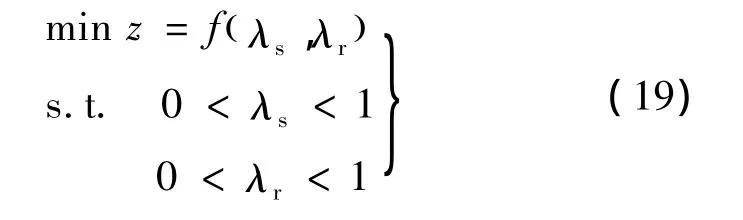
针对这种相邻双极并联驱动控制方式，并基于表1中给出的电机基本参数，采用指标(18)并求解式(19)的优化问题，对静电电机的输出平均力矩和力矩波动系数同时进行优化。

由于在第1节给出的可变电容静电微电机的数学模型不能获得解析表达式，解析求解式(12)表示的电机输出力矩很难实现，相应地，采用基于梯度或灵敏度分析的优化方法难以实现;这里采用遗传优化算法［9］。这种优化方法对优化问题的数学模型没有特殊要求，它采用交叉、复制、变异三种简单计算方法，能实现复杂空间中优化问题的求解，并能获得全局近似最优解。由于采用了数值积分方法计算式(9)给出的电容极板重叠面积，并采用有限差分方法计算式(11)表示的电机输出力矩，即使采用遗传算法这种比较耗时的优化方法，求解优化问题(19)时也有较快的速度。

4 实验结果

采用遗传算法，对设计参数进行优化后，电机定子电极和转子凸极的占空比取值变为(λs，λr)=(0.348，0.501)，对应的输出力矩如图8所示。

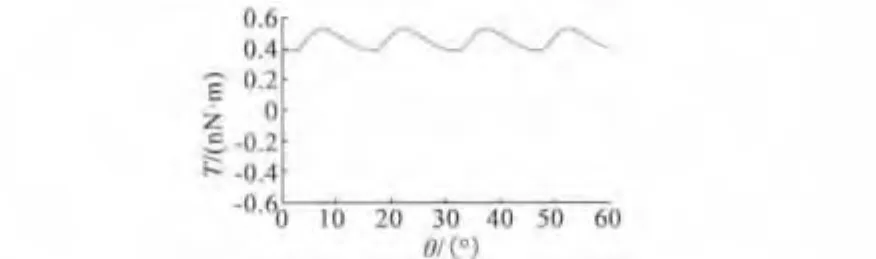
图8 相邻双极并联控制方式下，8/6电机结构参数优化后的输出力矩曲线

优化前后电机输出力矩如图9所示:优化后电机输出力矩均值变为4.0821×10－10N·m，比优化前减小9.84%，但是输出力矩的波动系数从33.04%降为9.41%。

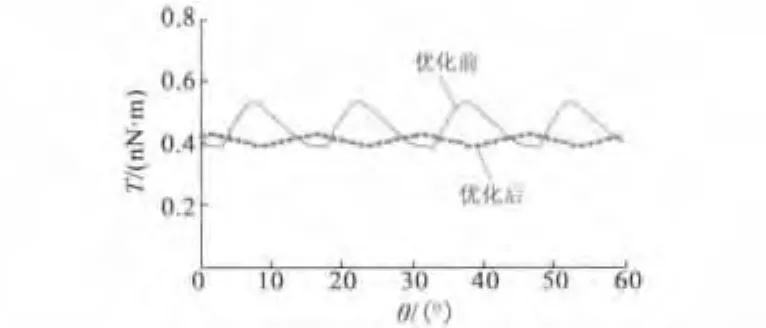
图9 优化前后8/6电机最大输出力矩的比较

5 结 语

本文针对顶面驱动可变电容静电微电机进行了优化设计，建立了其一般解析物理描述模型。以8/6静电微电机为例，进行了控制方式的优化，并采用数值积分方法和遗传优化算法相结合的算法对电机进行了结构参数优化，不但使电机的输出力矩明显增大，而且有效降低了它的波动，从而改善了电机的性能。这种优化设计方法，能快速进行顶面驱动可变电容静电微电机的优化设计，也更适合在MEMCAD等计算机辅助优化设计软件中应用。

［1］BACHMANN D，HIEROLD C.Determination of the pull－ off forces and pull－off dynamics of an electrostatically actuated silicon disk［J］.IEEE Journal of Microelectromechanical Systems，2008，17(3):643 －652.

［2］JUDY J W.Microelectromechanical systems(MEMS):fabrication，design and applications［J］.Smart Materials and Structures，2001，10(6):1115－1134.

［3］REBELLO K J.Applications of MEMS in Surgery［J］.Proceeding of the IEEE，2004，92(1):43 －55.

［4］LASER D J，SATIGO J G.A review of micropump［J］.Journal of Micromech.Microeng.，2004，14(6):35 －64.

［5］MEHREGANY M，TAI Y C.Surface micromachined mechanisms and micromotors［J］.Journal of Micromechanics and Microengineering，1991，1:73 －85.

［6］KETABI A，NAVARDI M J.Optimization of variable － capacitance micromotor using genetic algorithm［J］.Journal of Microelectromechanical Systems，2011，20(2):497 －504.

［7］BEHJAT V，VAHEDI A.Study the influence of geometric parameters on the torque of electrostatic micromotors［J］.Electrical Engineering，2006，89(1):61 －65.

［8］刘晓伟，何广平.可变电容静电型超微电机的优化设计［J］.微特电机，2012，40(12):48 －52.

［9］QUAGLIARELLA D，PERIAUX P，POLONI C，et al.Genetic algorithms and evolution strategy in engineering and computer science［M］.New York:John Wiley＆ Sons，1998.