船用螺旋桨三维建模方法研究

张 磊，吴小平，刘洋浩

（上海船舶研究设计院，上海 201203）

0 引 言

目前，螺旋桨仍然是经济性较好、应用最广的一种船舶推进器。设计者确定螺旋桨的设计参数后，需要加工桨模进行水池试验，或者运用计算机模拟对其性能计算分析。因此，快速建立精确、合理的三维模型显得非常必要。

1 螺旋桨几何特征

通常，设计螺旋桨需要确定其在不同半径处的弦长、最大拱度和最大厚度、螺距、侧斜和纵倾等轮廓参数的分布。此外，还需要已知其叶切面纵坐标的分布形式，如：系列图谱设计中，AU型、MAU型和B型螺旋桨叶切面的叶面、叶背纵坐标值直接以其最大厚度的百分比分布给出[1]；NACA系列则分别给出拱度、厚度沿弦长的分布[2]。

1.1 弦长

弦长是研究螺旋桨二维叶切面的一个基本特征，通常以此为横轴，给出拱线纵坐标和叶面、叶背纵坐标的分布，如图1，线段AB是弦线。

1.2 最大拱度和最大厚度

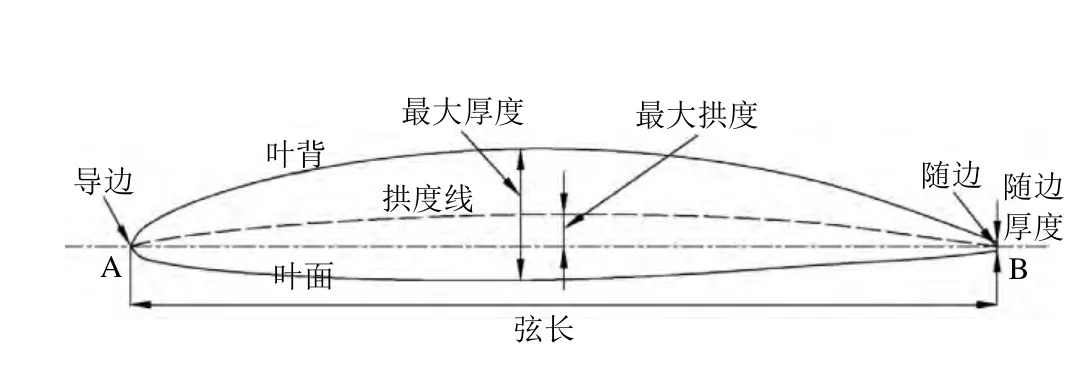
图1 二维叶切面

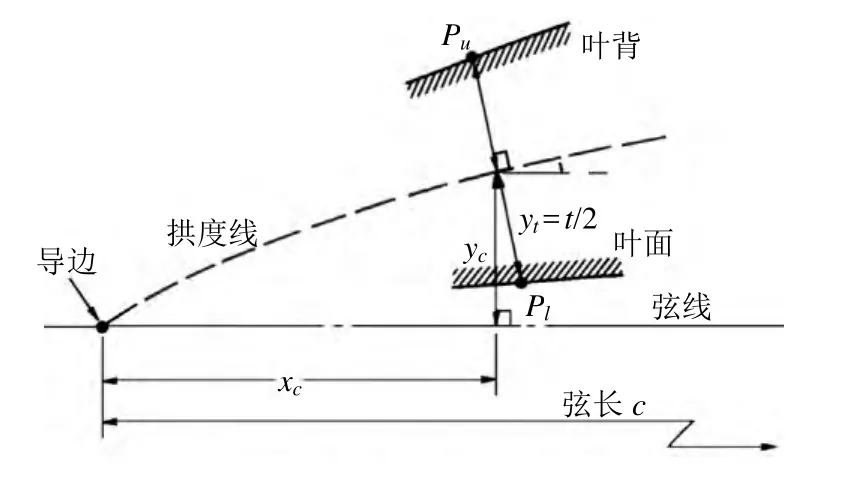
图2 NACA二维切面型值分布

以NACA翼型切面为例，如图1、2所示，由叶切面最大拱度和拱度分布可计算出该切面拱度沿弦长分布的纵坐标值，把这些坐标值用光顺曲线连接便是拱度线（或中拱线）。以最大厚度和厚度分布计算出该切面沿弦长分布的半厚度值。然后根据式（1）计算出上表面（叶背）和下表面（叶面）的坐标值[2]，由此可确定不同半径处的叶切面型值。

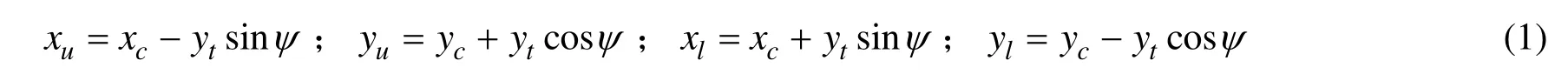
式中：(xu,yu)，(xl,yl)——距导边xc处对应点Pu、Pl的坐标；yc, yt——拱度纵坐标值、半厚度值；tanψ的值在拱度分布中给出。上式也可简化为式（2），其误差通常小于0.5mm，可满足大多数加工精度要求。

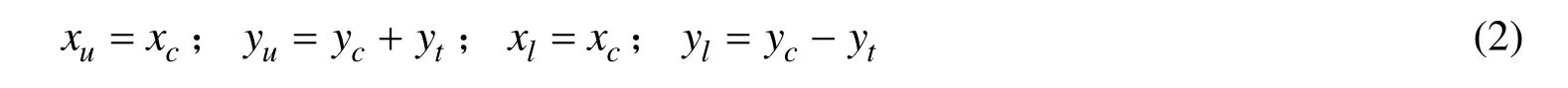
1.3 螺距

螺旋桨叶切面是螺旋面的一部分，任何与螺旋桨共轴的圆柱面与叶切面的交线为螺旋线的一段，将此线段延长且环绕轴线一周，则其两端之轴向距离等于此螺旋线的螺距[1]，如图3。通常，也用螺距角ntθ表示该半径处叶切面的倾斜程度。

1.4 侧斜和纵倾

弦长、最大厚度和最大拱度用于描述二维叶切面的特征，而螺距分布则定义了叶切面弦向与桨轴方向的夹角分布。在螺旋桨正投影图中，如图4，某半径处的侧斜角sθ定义为竖直参考线和桨轴中心与该半径处弦线中点的连线之间的夹角，连线偏向导边（即在竖直参考线右侧），sθ为负值，反之，为正值。sθ的最大值与最小值之差即为螺旋桨的侧斜角spθ，侧斜角确定的是叶切面在桨盘面周向的位置分布。

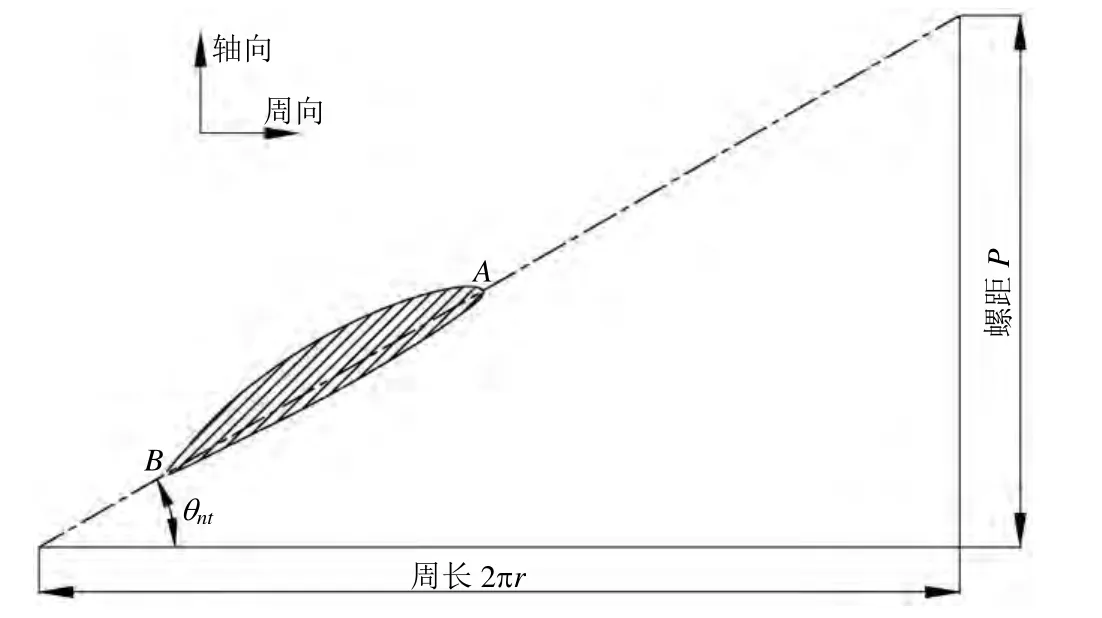
图3 螺旋桨的面螺距

纵倾确定了叶切面在桨轴方向的位置分布，图5为某半径处叶切面与叶根切面的相对位置关系，X为船首方向。总纵倾由两部分组成：一部分为以桨叶辐射基线定义的纵倾值iG；另一部分为侧斜引起的纵倾值is，总纵倾值为iT，偏向船尾取正值，关系如下：

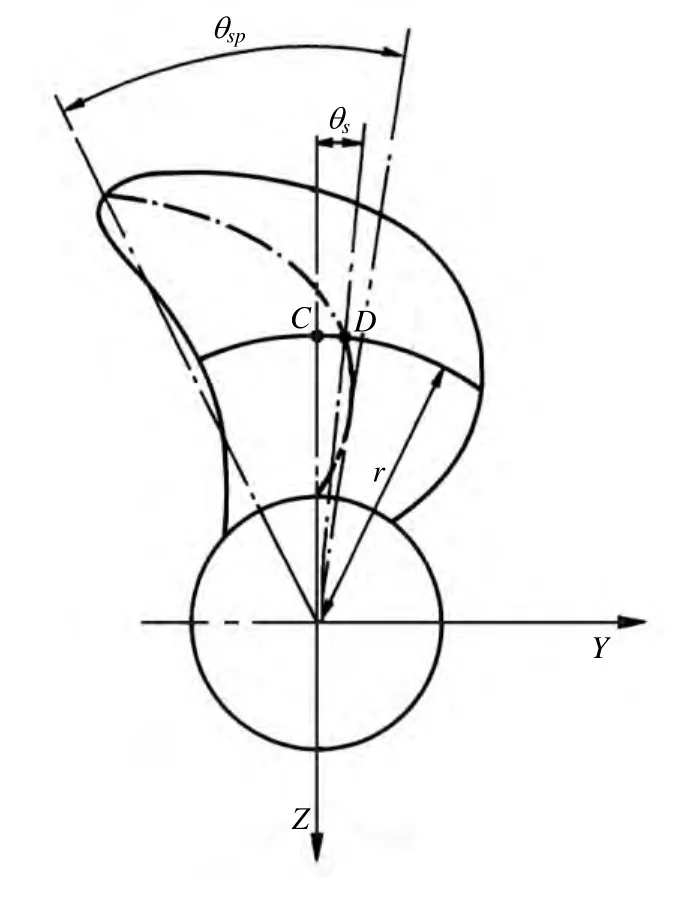
图4 螺旋桨侧斜定义

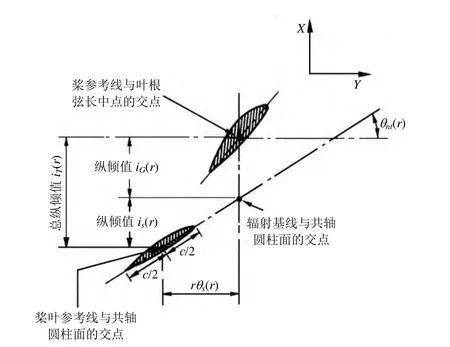
图5 螺旋桨纵倾定义

2 螺旋桨三维坐标计算

文献[3]给出了基于坐标变换方法的螺旋桨三维型值计算方法，已被一些学者所引用[4,5]。此方法定义了多个坐标系，通过多次坐标公式变换得到所需三维坐标。本文所用方法[2]，主要根据上文介绍的几何特征条件，通过分析几何投影关系给出坐标计算式，其精确度已得到实桨模型验证。以右旋桨为例，如图 6，定义坐标系x y z- - ，x为桨轴方向，指向船首为正；y轴水平且垂直于x轴，指向左舷为正；z由右手法则确定，由图6中几何关系可得三维坐标计算式（5）。

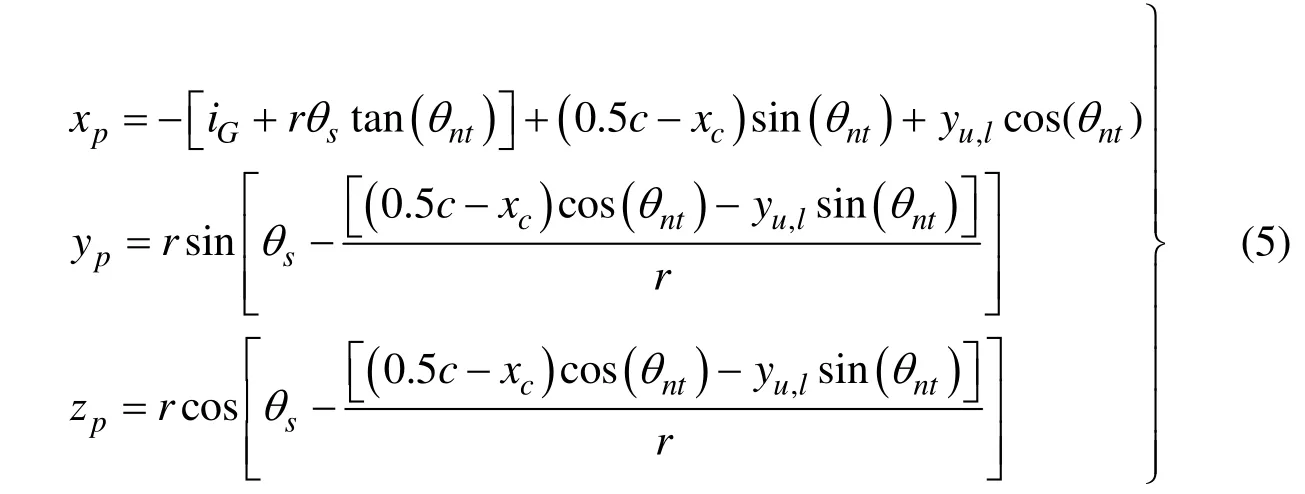
式中：(xp,yp,zp)——三维桨叶上任意一点的坐标；yu,l由式（1）或（2）计算得到；角度的单位均为弧度；纵倾iG和侧斜sθ的正负按本文1.4中的定义选取。

结合上文介绍几何特征参数及式（5），编写程序计算出三维坐标，具体流程如图7所示。

图6 桨叶表面任意点P的坐标定义

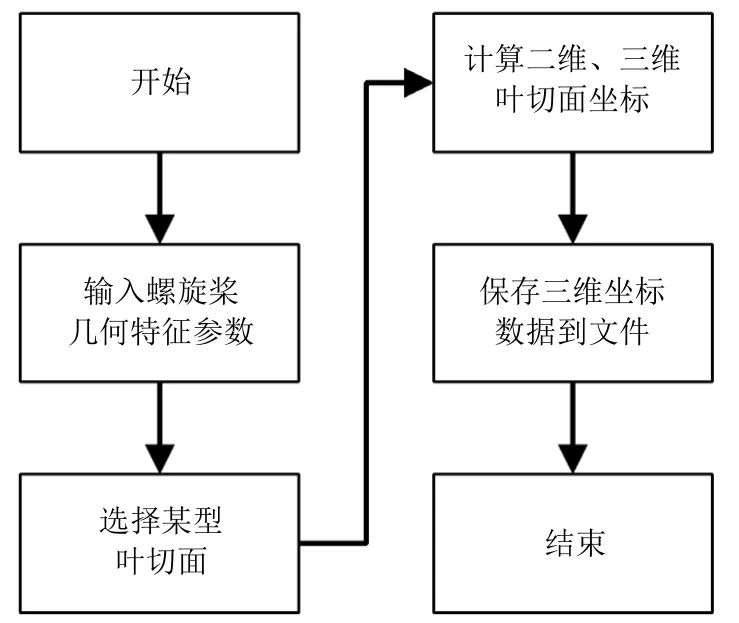
图7 三维坐标计算流程

3 螺旋桨三维建模实例

螺旋桨曲面构造复杂，为使所建模型更符合实际需求，应对一些细节部位进行特别处理。

1) 叶梢。在螺旋桨设计参数中，叶梢处（1.0R）的弦长很小，接近于零，但是厚度不为零，根据实际需要和经验，在建模时需要在叶梢处人为地给定一个弦长；

2) 随边。实桨的随边需要经过倒圆处理，同时螺旋桨为了抗谐鸣的发生，通常采取桨叶随边加厚或者减薄的方法[1]，以此来改变随边处涡旋引起的振动频率，避免其与桨叶固有频率发生共振。为了便于桨叶的机械加工（尤其小尺寸的桨模）和后期打磨切割处理，建模时可将随边略微加厚；

3) 叶根。按照船级社规范要求，桨叶叶根与桨毂相接的部位需要圆角过渡处理以减小应力集中，圆角半径的大小在各自规范中有所规定，如：BV规范[6]规定倒圆半径不小于3/4当地厚度，如图8所示，这样倒圆半径大小沿弦向是变化的；但规范对恒定的倒圆半径也可接受。在实际建模中，该倒圆角以叶切面最大厚度处圆角半径的恒定值处理，易于机械加工，也便于后期打磨加工。

以建立某散货船四叶桨模型为例，其方法步骤如下：

1) 通过文件中的三维坐标点生成样条线，得到各个叶切面轮廓线、导边和随边的轮廓线，如图9(a)；再通过曲线生成叶面、叶背、随边窄面、叶梢切面、叶根切面等；

2) 用第1）步生成的曲面建立桨叶实体；

3) 根据桨毂参数建立桨毂实体；

4) 对桨叶根部与桨毂相交的部位进行倒圆角处理，使其符合规范要求；

5) 将已建立好的桨叶绕桨毂复制旋转，得到另外三个桨叶实体，如图9(b)；

6) 将模型尺寸整体、均匀地缩放到所需尺寸。

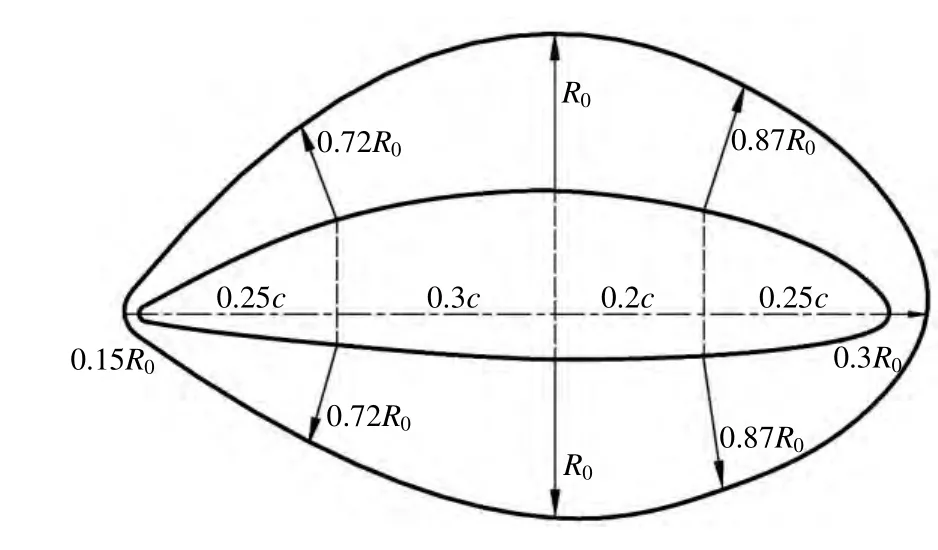
图8 倒圆半径沿弦向变化

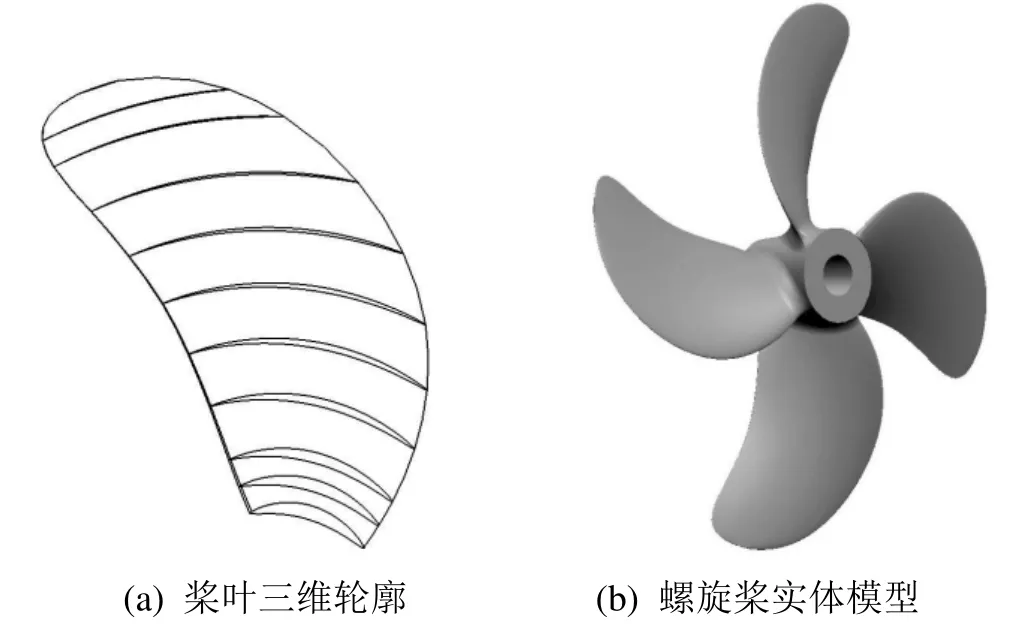
图9 桨叶三维轮廓与螺旋桨模型

4 结 语

本文分析了船用螺旋桨主要几何特征的意义，并介绍了计算桨叶三维坐标的方法。编写计算机程序，使得计算更加快捷、精确，为螺旋桨三维建模提供了数据基础。通过螺旋桨建模实例，介绍了特殊部位（如叶梢、叶根、随边等）的处理方法，使所建模型便于实际的生产加工和仿真计算应用；也给出螺旋桨三维建模的一般步骤以供参考。

[1] 盛振邦，刘应中. 船舶原理（下）[M]. 上海:上海交通大学出版社，2008.

[2] John C. Marine Propellers and Propulsion [M]. Butterworth Heinemann, 2011.

[3] 张宏伟，王树新，侯 巍，等. 螺旋桨三维建模方法研究[J]. 机床与液压，2006(5)：60-62.

[4] 唐 英，王志坚，杨 凯. 基于UG二次开发的船用螺旋桨参数化建模方法与实现[J]. 船舶工程，2010, 32(4)：52-55.

[5] 吴利红，董连斌，许文海. 基于MATLAB和ProE的螺旋桨三维建模[J]. 大连海事大学学报，2011, 37(2)：17-20.

[6] Veritas B. BV Rules for the Classification of Steel Ships[S]. 2011. Pt C, Ch1, Sec 8.