海底管道腐蚀模型对比研究
韩文海,周 晶
大连理工大学建设工程学部,辽宁大连 116024
0 引言
在恶劣的海洋环境条件下,海底管道不可避免会发生腐蚀损伤,严重时将引起管道断裂,造成原油泄漏,进而导致严重的环境污染和巨大的经济损失[1]。随着越来越多的海底管道进入使用阶段的中后期,输送介质对管道内壁的腐蚀已成为导致管道损坏的主要原因之一。定期对海底管道进行检测,对腐蚀管道进行可靠性计算和剩余寿命预测,对于延长管道寿命,降低维修费用,保证管道安全运行具有非常重要的意义[2]。
国内外许多学者对于腐蚀管道的可靠性研究和剩余寿命预测方面开展了一些工作。其中Teixeira等[3]、赵事等[4]采用一次二阶矩法对腐蚀管道的可靠性进行了研究;支希哲等[2]和Caleyo等[5]分析了管道的各项参数对腐蚀管道的灵敏度;俞树荣等[6]、帅健[7]、谭开忍等[8]建立了腐蚀管道的剩余寿命预测概率模型,进行腐蚀管道剩余寿命预测。在腐蚀管道的可靠性和剩余寿命研究中,大多数的文献都采用线性腐蚀模型来模拟海底管道腐蚀过程,基于失效应力建立极限状态方程,来计算腐蚀管道的可靠性,进行管道剩余寿命预测。而线性模型存在着一些问题,例如用线性模型来模拟管道腐蚀的非线性过程,不甚科学合理。而一些常用的非线性腐蚀模型,如幂函数模型和指数函数模型,却很少被用于研究腐蚀管道的可靠性。
本文详细介绍了线性腐蚀模型、幂函数腐蚀模型和指数函数腐蚀模型;基于最大腐蚀深度建立了腐蚀管道失效的极限状态方程;结合常用的腐蚀管道剩余强度方法(改进B31G、DNV和Shell方法),将幂函数模型和指数函数模型引入腐蚀管道的可靠性研究中;结合算例,采用Monte Carlo方法,对比研究了三种腐蚀模型及其对腐蚀管道失效概率的影响,并进行了腐蚀模型的参数敏感性分析。
1 管道腐蚀模型
管道在运行一定时间后,通常要进行检测,了解腐蚀情况,进行腐蚀参数统计。基于已有的资料建立腐蚀模型,对腐蚀进行预测是管道运行商的重要工作内容之一,同时也是国内外学者研究的热点。目前,基于已有的腐蚀资料建立腐蚀深度与腐蚀时间之间关系的模型主要有三类:线性模型、幂函数模型和指数函数模型。
1.1 线性腐蚀模型
线性模型认为对于稳态腐蚀过程,腐蚀深度是腐蚀时间的线性函数[9-10],线性模型如式(1)所示:

式中d(T)——腐蚀时间T时的腐蚀深度;
vd——腐蚀速率;
d0——腐蚀预测选定的初始深度。
若给定腐蚀检测资料:T1时最大腐蚀深度为d1(均值ud1,标准差σd1);T2时最大腐蚀深度为d2(均值ud2,标准差σd2)。则可求得:

根据误差传递定理可进一步求得vd的均值和标准差。通常取d0=d2,即基于最近的一次腐蚀资料建立腐蚀模型进行腐蚀预测。
由于模型简单,线性模型被大量用于海底管道可靠性计算和管道剩余寿命的预测中[1-8]。但是,线性模型自身存在着一些问题。海底管道的腐蚀是一个非线性过程,因此采用线性模型来模拟管道的腐蚀过程,从物理模型角度看,不甚科学合理。海底管道的腐蚀发生和发展与所处的海底环境密切相关。海底环境的变化使得准确地判断管道腐蚀是否处在稳态变得很困难,而稳态腐蚀是线性模型应用的前提条件,因此判断采用线性模型的时机同样困难。日常,只是根据经验判断来大致确定管道建成后若干年管道的腐蚀是否仍处于稳态,无法准确定量。同时,线性模型无法准确地推断出腐蚀发生的起始点。
1.2 幂函数模型
Velazquez[11]和Caleyo[12]等根据经验提出了一种非线性幂函数模型来模拟管道的腐蚀过程。在幂函数模型中,最大腐蚀深度表示为:

式中T0——腐蚀的时间初始点,即开始发生腐蚀与管道建成的时间间隔;
k——待定的比例系数;
a——待定的指数参数。
通常,综合考虑管道所处的海底环境和管道的防护措施,可以确定管道腐蚀的时间初始点T0。根据两次腐蚀检测资料可以计算出k和a的均值和标准差。
幂函数模型是最简单的非线性模型,相比线性模型可以更好地模拟腐蚀过程的非线性。
当T>T0时,幂函数模型才有意义,幂函数模型恰当地模拟了保护层破坏后管道才开始腐蚀的过程,从物理模型的角度说更加科学合理。T0的灵活选用,可以更多地考虑管道所处的海底环境和防护层材料等管道防护措施。所以幂函数模型可以更加灵活、合理地模拟腐蚀过程。
1.3 指数函数模型
指数函数模型是指腐蚀管道管壁剩余壁厚与时间之间成指数关系[13],指数函数模型表示的最大腐蚀深度见下式:

式中t——完好管道管壁的厚度;
G和h——待定的比例系数。
指数函数模型也是一种简单的非线性模型,也可以很好地模拟腐蚀过程的非线性。指数函数模型拥有和幂函数模型一样的优点。同时,指数函数模型可以更好地模拟管道的电化学腐蚀过程[14]。
1.4 算例
某海上油气田于1997年建成,在2007年和2012年进行了两次大规模检测,进行统计分析后得到管道的最大腐蚀深度见表1。根据线性模型、幂函数模型和指数模型拟合出最大腐蚀深度随服役年限变化曲线见图1(取2012年为腐蚀预测选定的初始点)。由同一腐蚀资料(表1)拟合的线性模型、幂函数模型和指数函数模型,在相同服役时间时,指数函数模型的最大腐蚀深度偏小,幂函数模型偏大。并且,随服役时间的延长,三种模型之间的差距逐渐增大。

表1 管道的最大腐蚀深度

图1 最大腐蚀深度随服役年限变化的曲线
2 基于可靠性的管道腐蚀模型对比
2.1 腐蚀管道失效的极限状态方程
管道发生腐蚀后,管道的强度和承载能力会降低。一般来讲,管道的失效压力主要取决于下列参数:

式中Pf——腐蚀管道的失效压力;
D——管道外径;
t——管道壁厚;
d——腐蚀缺陷最大深度;
L——腐蚀缺陷最大长度;
b——腐蚀缺陷最大宽度;
σ——管道的材料强度。
一般而言,腐蚀缺陷在深度方向的生长率随时间变化较大,而在长度方向上随时间变化不大,因此假定长度方向的缺陷生长率近似为0[15]。已知管道的操作压力为Pop,令Pf=Pop,则可以求得在操作压力下腐蚀管道的临界腐蚀缺陷深度dlim。则腐蚀管道失效的极限状态方程为:

式中LSF(d,T)——腐蚀管道失效的极限状态函数。
当LSF(d,T)为正 (dlim>d(T)) 时,管道安全运行;反之,若LSF(d,T)为负 (dlim<d(T)) 时,管道失效。
2.2 管道剩余强度评价方法
运用式(6)腐蚀管道失效极限状态方程计算腐蚀海底管道的可靠性,需要根据管道的操作压力Pop,结合失效压力Pf的表达式(管道剩余强度评价方法),求出腐蚀管道的临界腐蚀缺陷深度。基于试验和数值方法,国内外学者已对管道剩余强度评价方法进行了大量的研究,提出了许多评价方法。其中,国际上著名的腐蚀管道剩余强度评价方法有美国的ASME B31G、改进的ASME B31G、Battele、Shell-92以及挪威船级社的DNV-99等[16]。本文为突出研究的广泛性,选用多种腐蚀管道剩余强度评价方法进行研究,如改进的ASME B31G、DNV-99和Shell-92。
(1) 改进的ASMEB31G:

式中 σy——管道材料的屈服强度/MPa;
M——Foilas系数。
(2) DNV-99:
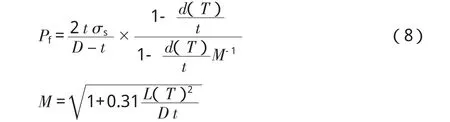
式中 σs——管道材料的极限抗拉强度/MPa。
(3) Shell-92:

2.3 算例分析
1.4算例中的油气田所用海底管道参数见表2。最大腐蚀深度所对应的腐蚀缺陷长度变化不大,均取为203.2mm(标准差6.07mm)。根据上述数据,采用M onte Carlo方法对管道进行失效概率计算,得到的腐蚀管道失效概率随服役年限的变化曲线(取2012年为腐蚀预测的零点),见图2~图4。

表2 海底管道参数

图2 采用改进B31G方法计算结果
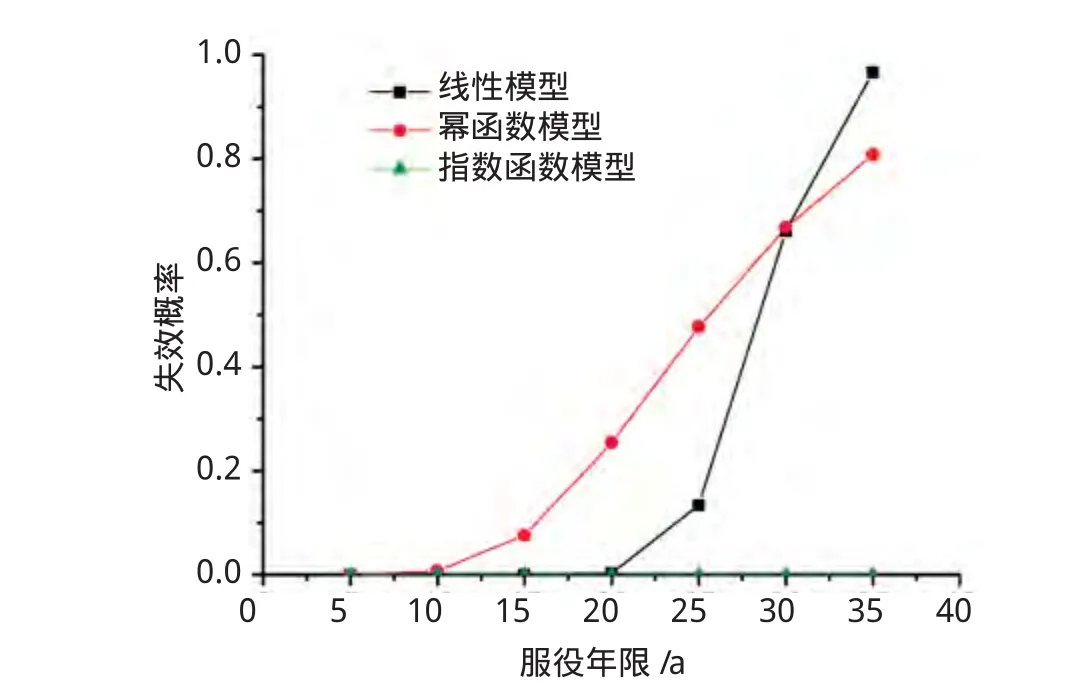
图3 采用DNV方法计算结果

图4 采用She ll方法计算结果
由图2~图4可知,基于不同剩余强度的评价方法,三种腐蚀模型的失效概率-服役时间曲线的变化趋势大致相同,即失效概率随服役时间的增加而增加。相比于指数函数模型,通过线性模型和幂函数模型计算的失效概率比较接近。对比三种腐蚀模型,幂函数模型失效概率曲线的变化比较平缓,能更好地反映腐蚀海底管道随服役时间增加,腐蚀加剧,可靠性逐渐丧失,失效概率逐渐增加的实际。在腐蚀预测零点之后的一段时间内(20年内),通过幂函数模型计算的失效概率大于其余两种腐蚀模型,说明幂函数模型比较保守。对于处于恶劣海洋环境中的海底管道,幂函数模型的保守性对于保障海底管道的安全运行是有益的。在较长的一段时间(25至30年)后,线性模型的失效概率逐渐超过幂函数模型。但是对于较长时间腐蚀后的预测通常与现实差距较大,是不准确的,仅可用于参考。当选用的腐蚀模型一定时,可见在同一服役年限,Shell方法的失效概率(见图4)显著大于DNV和改进B31G方法(见图3、图2),说明Shell方法较保守。
3 腐蚀模型的敏感性分析
一般而言,腐蚀缺陷在深度方向的生长率随时间变化较大,而在长度方向上随时间变化不大[15]。同时,已有文献[17]验证了腐蚀海底管道的失效概率对腐蚀深度变化比较敏感。因此选用腐蚀深度作为基本随机变量,结合以上算例,进一步分析了腐蚀模型对参数的敏感性。因Shell方法较保守,这种保守对保障海底管道的安全运行是有益的,所以在对腐蚀模型敏感性分析中将采用Shell方法。相比于指数函数模型,线性模型和幂函数模型比较接近,也较为保守,因此着重研究线性模型和幂函数模型的参数敏感性。
在蒙特卡洛方法中,一般文献给出的敏感性指标计算方法过于复杂,无法用解析法求解。这里借鉴故障树分析法中计算基本事件临界重要度的方法来进行参数的敏感性分析[18]。定义敏感性指标为:

式中 αi——随机变量Ci的敏感性指标;
Ci——基本随机变量;
△Ci——随机变量变化;
Pf——结构的失效概率;
△Pf——对应△Ci引起的结构失效概率的变化。
结合算例1.4和算例2.3,表1中2012年最大腐蚀深度的检测值精度不变(即标准差不变),均值增大5%,即由2.84变为2.84×(1+5%)=2.98。计算线性模型和幂函数模型对应的失效概率的变化,进而求得两种腐蚀模型对应的敏感性指标,见表3。

表3 敏感性指标α随服役时间变化
由表3中的敏感性指标可知,对于线性模型,敏感性指标最大值αmax=69.52。对于幂函数模型,敏感性指标最大值αmax=14.46,远小于线性模型。可见,当最大腐蚀深度检测值出现误差时,采用幂函数腐蚀模型计算的腐蚀海底管道失效概率变化较小。幂函数模型对参数的不敏感性使其能够更好地用于海底腐蚀管道的可靠性分析。
4 结论
本文系统地介绍了常用的腐蚀模型:线性模型、幂函数模型和指数函数模型,详细分析了三种腐蚀模型的优缺点,并将幂函数模型和指数函数模型引入腐蚀管道可靠性计算中。基于腐蚀管道的最大腐蚀深度建立了腐蚀管道失效的极限状态方程,结合常用的管道剩余强度评价方法,通过算例,分析了腐蚀模型对海底腐蚀管道可靠性计算结果的影响,得到如下结论:
(1)基于最大腐蚀深度的极限状态方程可以方便地与腐蚀深度检测和腐蚀模型联系起来,进行腐蚀管道可靠性计算。
(2)对于初期的腐蚀预测,与其余两种模型相比,通过幂函数模型计算的失效概率较保守,幂函数模型的这种保守性有益于保障海底管道的安全运行。
(3)当选用的腐蚀模型一定时,在同一服役年限,Shell方法相比于DNV和改进B31G方法更为保守,适合用来计算海底腐蚀管道的可靠性。
(4)通过对线性模型和幂函数模型进行参数敏感性分析,得到幂函数模型计算的海底腐蚀管道失效概率对于最大腐蚀深度的变化较不敏感。相比于线性模型,幂函数模型更适合用来进行海底腐蚀管道可靠性分析。
综上,幂函数模型可以综合考虑管道所处的海底环境和防护层材料等管道防护措施。同时幂函数模型具有灵活性、非线性、保守性和对参数的不敏感性。相比线性模型和指数函数模型,幂函数模型更适合用于海底腐蚀管道的可靠性计算。因此,在海底腐蚀管道研究和实际工程中,推荐使用幂函数模型代替线性模型,同时结合Shell方法来计算腐蚀管道可靠性和进行腐蚀管道剩余寿命预测。
[1]李国辉,闰术明,尤伟星.含有单个腐蚀缺陷的海底管道剩余强度评估[J].石油工程建设,2011,37(4):27-32.
[2]支希哲,周红,何洁.腐蚀管道剩余寿命及参数灵敏度分析[J].西北工业大学学报,2011,29(6):983-986.
[3]Teixeira A P,Guedes C Soares.Reliability of Pipelines with Corrosion Defects[J].International Journal of Pressure Vessel and Piping,2008,85(6):228-237.
[4]赵事,蒋晓斌,高惠临.腐蚀管道的失效概率和剩余寿命预测方法[J].油气储运,2006,25(12):28-31.
[5]Caleyo F,Gonzale J L,Hallen J M.A Study on the Re liability Assessment Methodology for Pipe lines with Active Corrosion Defect[J].International Journal of Pressure Vessel and Piping,2002,79(10):77-86.
[6]俞树荣,李建华,李淑欣,等.埋地管道腐蚀剩余寿命预测概率模型[J].中国安全科学学报,2008,18(6):11-15.
[7]帅健.腐蚀管线的剩余寿命预测 [J].石油大学学报(自然科学版),2003,27(4):91-93.
[8]谭开忍,肖熙.基于灰色理论的海底管道腐蚀剩余寿命预测方法[J].上海交通大学学报,2007,41(2):186-193.
[9]Ahamm ed M,Melchers R E.Reliability estimation of pressured pipe lines subjected to localized corrosion defects[J].Pressure Vessels,1996,16(5):267-272.
[10]Ahamm ed M.Probabilistic estimation of remaining life of a pipeline in the presence of active corrosion defect[J].Pressure Vessels,1998,15(6):321-329.
[11]Velazquez JC,Caleyo F,Valor A,et al.Predictive model for pitting corrosion in buried oil and gas pipe lines[J].Corrosion,2009,65(9):332-342.
[12]Caleyo F,Velazquez J C,Hallen J M.Probability distribution of pitting corrosion depth and rate in underground pipelines:a Monte Carlo study[J].Corrosion,2009,51(7):1 925-1 934.
[13]俞蓉蓉,蔡志章.地下金属管道的腐蚀与防护时[M].北京:石油工业出版社,1998.
[14]袁赓.油气管道的腐蚀及预测研究[D].大连:大连理工大学,2011.
[15]Sheikh A K,Boah JK,Hansen D A.Statistical modeling of pitting corrosion and pipeline reliability[J].Corrosion,1990,46(3):3-8.
[16]帅健,张春娥,陈福来.腐蚀管道剩余强度评价方法的对比研究[J].天然气工业,2006,26(11):122-126.
[17]董玉华,余大涛,高惠临.含缺陷油气管线结构失效概率计算方法比较[J].机械强度,2006,28(1):118-122.
[18]章国栋,陆延孝,屠庆慈,等.系统可靠性与维修的分析与设计[M].北京:北京航空航天大学出版社,1990.

