燃烧模型对多孔介质内预混燃烧的影响

夏永放，史俊瑞，徐有宁，李本文，薛治家，谷聪伟

(1.沈阳工程学院 辽宁洁净燃烧发电与供热技术重点实验室，辽宁 沈阳 110316；2.大连理工大学 能源与动力学院，辽宁 大连 116024)

燃烧模型对多孔介质内预混燃烧的影响

夏永放1，史俊瑞1，徐有宁1，李本文2，薛治家1，谷聪伟1

(1.沈阳工程学院 辽宁洁净燃烧发电与供热技术重点实验室，辽宁 沈阳 110316；2.大连理工大学 能源与动力学院，辽宁 大连 116024)

采用二维非稳态数学模型研究燃烧模型多孔介质内预混燃烧影响.燃烧模型分别为单步和多步化学反应动力机理(17种组分，58个反应)，CH4/空气当量比的范围为0.55～1.0.对比分析两种燃烧模型下燃烧器中心处的温度、组分浓度分布曲线.结果表明，多步燃烧模型对燃烧器内温度、组分浓度分布有更准确的预测，并与文献结果比较，证实了二维非稳态数学模型的正确性.此外，将二维的温度场进行比较，结果表明单步化学机理的反应区域小，温度梯度大，而多步化学反应由于各反应步骤存在时间尺度的差异，反应区域大，温度梯度相对较小，与实际燃烧情况能很好的吻合.

燃烧模型；预混燃烧;多孔介质;二维数值模拟

预混气体燃烧特性研究一直被许多学者作为一个热门的话题[1-2].多孔介质内预混气体燃烧具有低CO和NOx排放、热流密度高及动力调节范围大等优点，可应用在内燃机、户式供暖、工业炉等领域[3-4].近些年，在多孔介质预混燃烧器设计和运行上有了更多的研究.Fu，Hsu等[5-6]在多孔介质内燃烧的辐射效率、燃烧率、熄火极限、火焰稳定性、污染物排放等方面做了大量的试验工作.数值模拟被广泛用在研究多孔介质燃烧方面.Hsu等[7]对多孔介质内的燃烧速度、温度、组分浓度分布做了一维数值计算，确认使用多步化学反应动力模型的必要性.Barra等[8-9]首次用一维非稳态数学模型研究了多孔介质内气固传热过程及多孔介质材料特性对火焰稳定性的影响.Brenner等[10]用二维稳态数学模型对多孔介质燃烧器内温度场及组分浓度分布进行了数值模拟，并与实验数据进行比较，认为数值模拟是很好的辅助设计工具.Liu等[11]用二维非稳态数学模型研究了多孔介质燃烧器内反应物当量比、介质辐射衰减系数及导热系数对温度场的影响.

采用二维非稳态数学模型，分别用单步和多步化学反应(17种组分，58个反应)机理，对CH4/空气当量比Φ在0.55～1.0范围内进行数值计算.分析比较两种燃烧模型对温度场、组分浓度分布引起的差异.此外，对两种燃烧模型下多孔介质燃烧器的排放温度进行分析，并与文献[7-8]数据进行比较来验证计算模型及结果的正确性.同时，还研究CO浓度随当量比Φ的变化规律，并与文献[12]结果进行比较，进一步证实计算模型及结果的正确性.

1 数值模拟模型

1.1 物理模型

研究对象为2段式柱形多孔介质燃烧器，数值计算区域为燃烧器模型对称轴的一半，模型如图1所示.

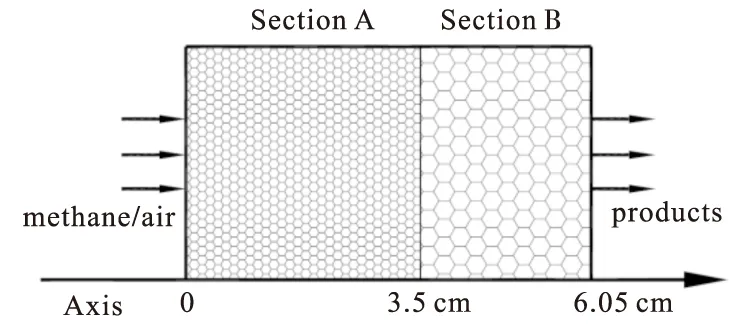
图1 多孔介质燃烧器模型

燃烧器总长度6.05 cm，上游段小孔区A(Al2O3,25.6 ppc(单位厘米孔数))长度为3.5 cm，下游段大孔区B(PSZ(氧化钇稳定的氧化锆),3.9 ppc)[7]长度为2.55 cm，燃烧器内径为7 cm.

1.2 数学控制方程

为简化计算工作量，做如下假设.

1) 燃气混合物为理想气体且无辐射.

2) 多孔介质材料常物性且无催化作用.

3) 忽略Dufour效应、Soret效应及体积力.

4) 燃烧器壁面绝热.

5) 忽略浮升力效应.

基于以上假设，采用二维非稳态数学模型，控制方程组如下.

1)连续性方程

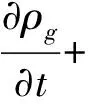
(1)

2)动量方程

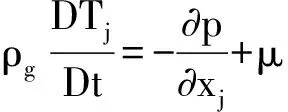
(2)

3)气体能量方程

(3)

4)固体能量方程

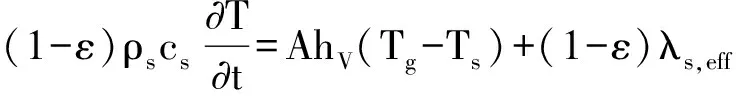
(4)

5)组分输运方程

(5)

式中，ρg为气体混合物密度，uj为气流速度，p为压力，μ为气体混合物动力粘性系数，ε为多孔介质空隙率，cg为气体混合物平均比热容，Tg为气体热力学温度，Ts为固体温度，λg为气体导热系数， cg,k为第k种组分的比热容， Dk为第k种组分的扩散系数，Yk为第k种组分质量分数，ωk为第k种组分生成率，hk为第k种组分生成焓，hV为体积对流换热系数，ρs为固体密度，cs为固体比热容，λs,eff为有效固体导热系数.Vk,j为第k种组分扩散速度.

有效固体导热系数λs,eff=λs+λR，其中λs为固体导热系数，λR为当量辐射导热系数.多孔介质假定为连续性介质且光学厚度为无穷大，当量辐射导热系数由扩散逼近法确定[11,13]：

(6)

固相能量方程通过固气相间的对流换热进行耦合求解.由于传热的复杂性换热系数采用体积对流换热系数，体积Nusselt数一般关系表达式如下[8]：

Nuv=CRem

(7)

式中，常数C在小孔区和大孔区分别为0.638、0.146，指数m在小孔区和大孔区分别为0.42、0.96.

为了使计算方程组封闭，气相混合物密度需要计算，其表达式如下：

(8)

第k种组分的扩散速度计算表达式如下：

(9)

式中，Dkm组分扩散系数从CHEMKINII物性输运数据库获得[17].

1.3 燃烧模型和边界条件

模拟计算燃烧模型分别使用单步燃烧模型和多步燃烧模型(17种组分，58个反应)[7].此研究采用二维非稳态数学模型，初始条件预设多孔介质燃烧器内点火温度为1 500K，气体混合物入口边界条件为

T0，in=298K,u=0.6m·s-1,v=0,Yk=Yk,in

出口边界条件为

假设进出口多孔介质与环境间仅存在辐射换热，其入口表达式为

出口为

2 计算方法

计算使用CFD软件包FLUENT6.3，气固两相及燃烧器进出口与环境间的换热计算采用自定义函数UDF程序完成，气体组分热化学及输运特性由CHEMKIN II物性输运数据库[14]和TRANFIT数据库获得[15].用SIMPLE算法对压力速度场耦合计算，对流相离散采用一阶迎风差分格式，扩散项采用中心差分格式.

3 结果与讨论

使用两种燃烧模型分别在当量比Φ=0.55～1.0范围内进行二维数值计算，分析比较单步和多步化学反应机理对温度场、组分浓度分布引起的差异.另外，对多步反应中CO排放浓度与当量比变化规律进行分析.

为了验证二维非稳态数学模型的正确性，绘制出不同当量比下单步和多步反应燃烧器轴中心温度及主要组分分布曲线，并进行比较，如图2所示.

由于燃烧器内气体和固体间的对流换热系数较高，气体和固体间温差较小，因此，固体温度曲线不作详细分析.在预热段固体间进行导热及辐射方式传热，其温度稍高于气体；而在反应区，燃烧气体放出化学反应热，温度稍高于固体.图2表明在预热区单步反应与多步反应的温度及主要组分分布曲线是基本重合的，而在反应区段，单步反应的温度比多步反应的温度要高，温度梯度大，而且单步反应主要组分浓度也比多步反应组分浓度要高.由于单步反应无法选择化学反应路径，反应区域小，CO2生成速度要比多步反应快.相比之下，多步反应机理中CH4热解成中间碳氢化合物组分，从化学反应时间尺度来分析，燃料氧化反应生成CO和CO2速度比单步化学反应机理慢.在反应区CO出现峰值，随后部分CO组分又被氧化成CO2，多步反应释放的化学反应热比单步反应少，因此，多步反应的出口温度比单步反应低.图2还表明，随当量比Φ增加，以上对应各相同量的差值加大，与文献[7]具有相似的规律.

两种反应机理情况下多孔介质燃烧器出口温度随当量比Φ变化关系，如图3所示，并与文献[8]进行比较.当量比Φ增加，出口温度近似地呈线性升高，与文献[8]具有相同的规律.随当量比Φ增加，单步反应与多步反应出口温度差值逐渐加大.在当量比Φ=0.8时，多步化学反应的出口温度几乎与文献[8]的结果相等，证明此研究采用二维非稳态数学模型的正确性.

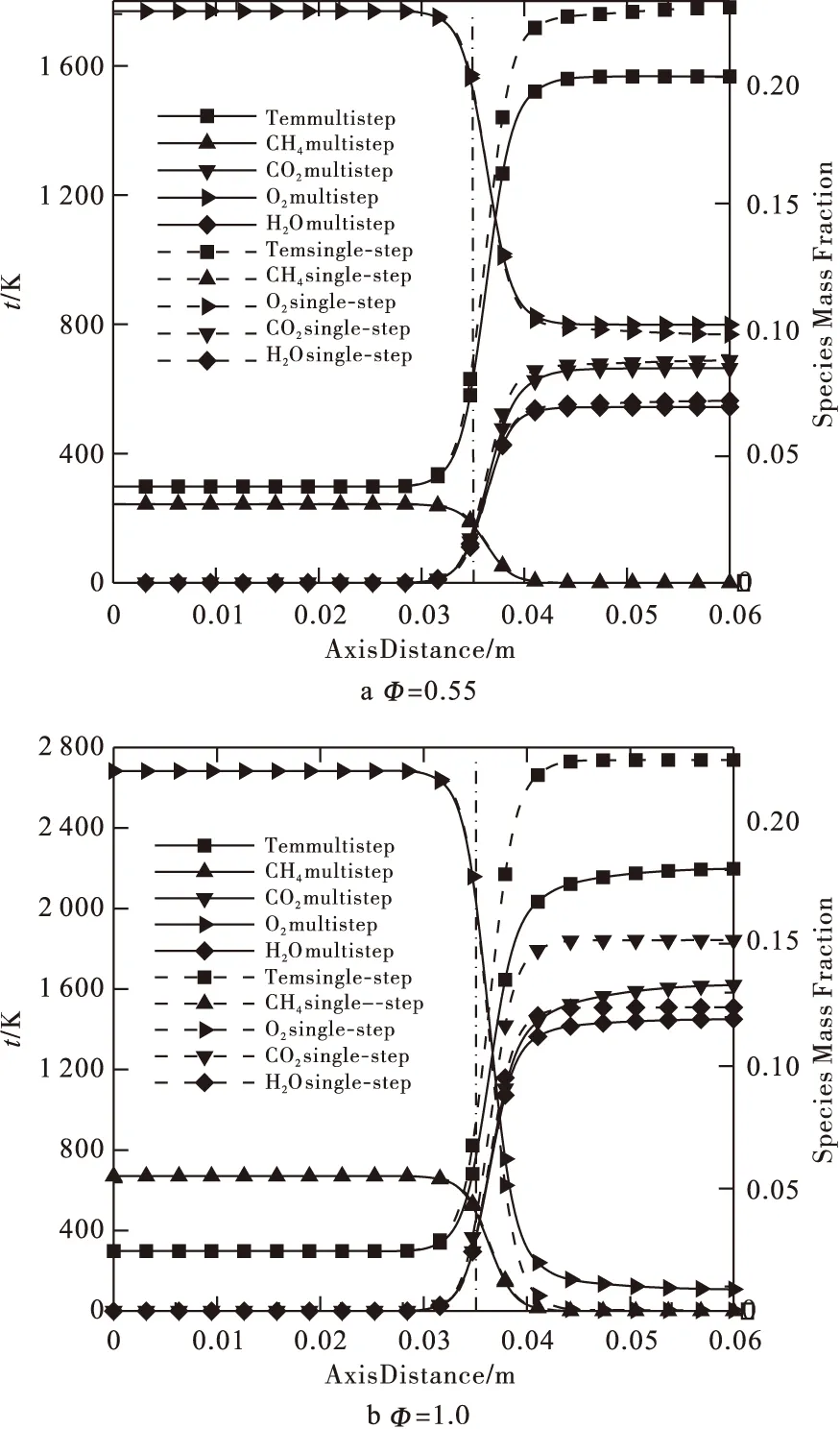
图2 不同当量比单步和多步化学反应机理的温度、组分浓度曲线比较

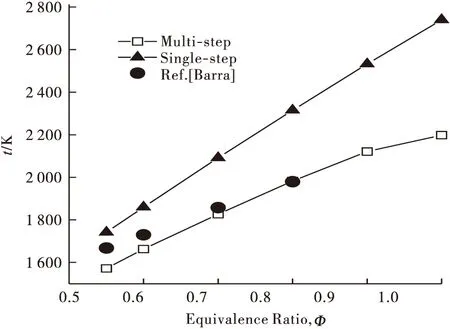
图3 单步和多步化学反应机理排放温度比较

不同当量比下二维CO浓度分布云图，如图4所示.从图4中可以看出上下游多孔介质交界面上CO有很大的变化梯度，出现峰值浓度；随后，部分CO又被氧化成CO2，浓度降低.随着当量比Φ增加，CO的峰值浓度升高，排放浓度增加.燃烧器中心CO排放浓度随当量比Φ的变化关系曲线，如图5所示.CO出口排放浓度随当量比Φ呈近似幂指数变化，并与文献[12]结果进行比较，表明二维非稳态模型计算结果能够与文献实验结果吻合较好，进一步证实了研究数学模型及燃烧模型的正确性.

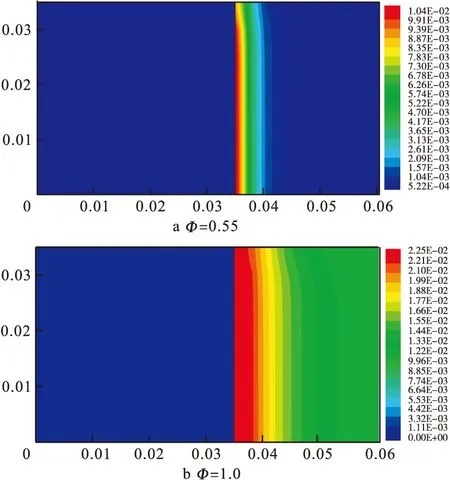
图4 当量比Φ=0.55和Φ=1.0的CO质量浓度分布云图

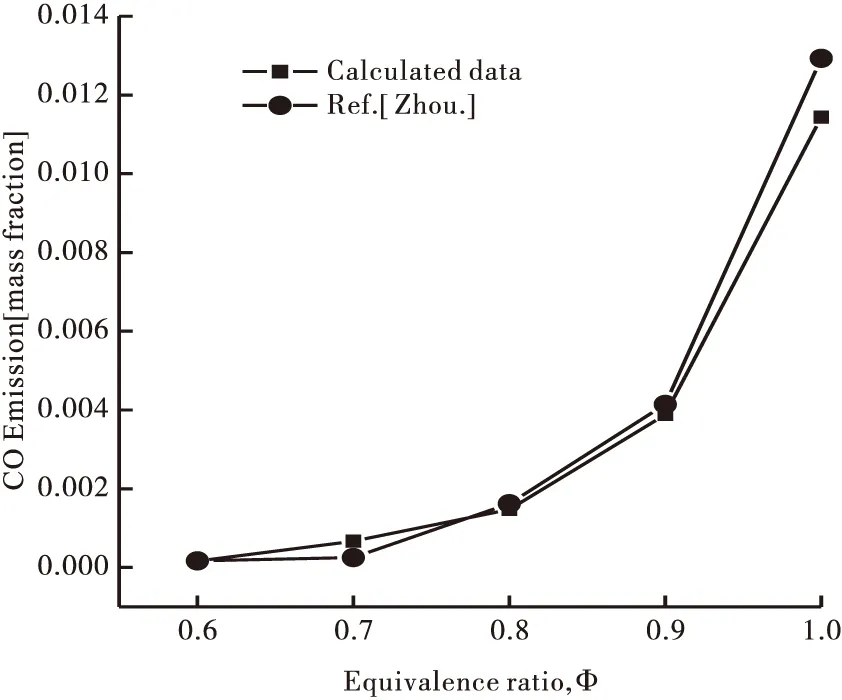
图5 CO排放浓度计算数据与实验比较

不同当量比时，2种燃烧模型的二维温度场比较，如图6所示.由于单步化学反应模型反应迅速，反应区域小，在较小空间区域内，有较大的温度梯度.而对于多步化学反应模型，由于化学反应路径多，各反应步骤存在反应时间尺度上的差异及中间组分的不完全反应，具有较大的反应区域，温度梯度较小，温度场分布更均匀化一些，更接近实际情况.此外，燃烧器壁面处由于气体粘滞力的影响，在边界上存在流动边界层，温度分布符合边界层规律.

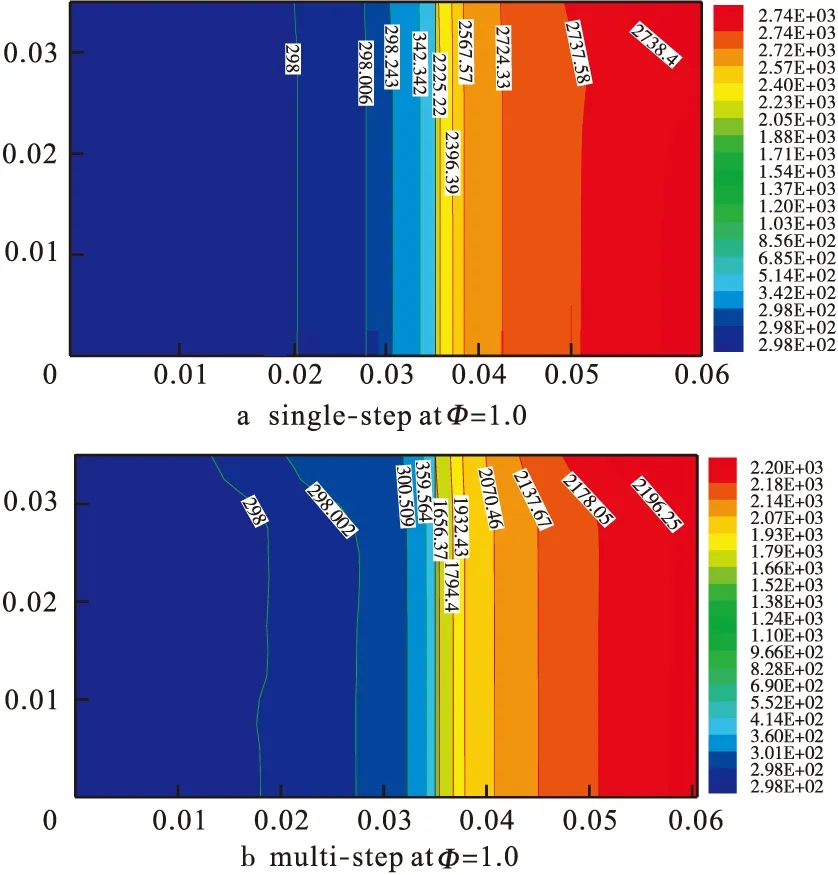
图6 不同当量比单步反应与多步反应机理的温度场比较

4 结 论

通过采用二维非稳态数学模型对单步燃烧模型和多步燃烧模型计算结果分别进行计算分析比较，得到如下主要结论.

1)计算结果与文献[7-8，12]数据相吻合，证实了此研究采用二维非稳态数学模型是正确的.

2)单步燃烧模型反应迅速，反应区域小，而多步燃烧模型各个反应步聚存在反应时间尺度的差异，整体反应较平缓，反应区域较大，接近于实际燃烧规律.

3)相对于单步燃烧模型，多步燃烧模型能够预测污染物形成规律及排放浓度，CO排放浓度随当量比Φ呈幂指数增加.

[1] Jun-Rui Shi,Mao-Zhao Xie,Hong Liu,et al.Two-dimensional numerical study of combustion and heat transfer in porous media combustor-heater[J].Proceedings of the Combustion Institute,2011,33: 3309-3316.

[2] 刘慧，董帅，李本文，等.多孔介质内预混气体燃烧稳定操作范围的研究[J].东北大学学报：自然科学版，2010，31(6)：834-837.

[3] D Trimis,F Durst.Combustion in a porous medium-advances and applications[J].Combustion Science and Technology,1996,121:153-168.

[4] J R Howell,M J Hall,J L Ellzey.Combustion of hydrocarbon fuels within porous inert media[J].Progress Energy Combustion Science,1996,22:121-145.

[5] X Fu,R Viskanta,J P Gore.Measurement and correlation of volumetric heat transfer coefficients of cellular ceramics[J].Experimental Thermal and Fluid Science,1998,17:285.

[6] P F Hsu,W D Evans,J R Howell.Experimental and numerical study of premixed combustion within nonhomogeneous porous ceramics[J].Combustion Science and Technology,1993,90:149-172.

[7] P F Hsu,R D Matthews.The necessity of using detailed kinetics in models for premixed combustion within porous media[J].Combustion and Flame,1993,93:457-466.

[8] Amanda J Barra,Guillaume D,Janet L E,et al.Numerical study of the effects of material properties on flame stabilization in a porous burner[J].Combustion and Flame,2003,134:369-379.

[9] Amanda J B,Janet L.Heat recirculation and heat transfer in porous burners[J].Combustion and Flame,2004,137:230-241.

[10]G Brenner,K Picken,O Picken,et al.Numerical and experimental investigation of matrix-stabilized methane/air combustion in porous inert media[J].Combustion and Flame,2000,123: 201-213.

[11]Hui Liu,Shuai Dong,Benwen Li,et al.Parametric investigations of premixed methane-air combustion in two-section porous media by numerical simulation[J].Fuel,2010,89:1736-1742.

[12]X Y Zhou,J C F Pereira.Comparison of four combustion models for simulating the premixed combustion in inert porous media[J].Fire Mater,1998,22: 187-197.

[13]Maozhao Xie,Junrui Shi,Yangbo Deng,et al.Experimental and numerical investigation on performance of a porous medium burner with reciprocating flow[J].Fuel,2009,88:206-213.

[14]R J Kee,F M Rupley,J A Miller.The Chemkin thermodynamic data-base[R].Sandia National Laboratories Report,SAND-8215B,1992.

[15]R J Kee,G Dixon-Lewis,J Warnatz,et al.A fortran computer code package for the evaluation of gas phase multi-component transport properties[R].Report SAND86-8246,Sandia National Laboratories,1986.

EffectofCombustionModelonPremixedCombustionwithinPorousMedia

XIAYong-fang1,SHIJun-rui1,XUYou-ning1,LIBen-wen2,XUEZhi-jia1,GUCong-wei1

(1.KeyLaboratoryofCleanCombustionforElectricGenerationamp;HeatingTechnologyofLiaoning,ShenyangInstituteofEngineering,Shenyang110136,LiaoningProvince;2.SchoolofEnergyamp;PowerEngineering,DalianUniversityofTechnology,Dalian116024,LiaoningProvince)

The effect of combustion model on premixed combustion within porous media is investigated by using two-dimensional unsteady mathematical model.The combustion models include single-step and multi-step (17 species,58 reaction steps) reaction kinetics mechanisms and methane/air equivalence ratios (Φ) range from 0.55 to 1.0.The calculated data of temperature and species concentration profiles on the centerline of burner are analyzed and compared for different combustion models,The results indicate that the predictions of both temperature and species concentration are more accuratewhen using multi-step chemical reaction mechanism.And the data are also compared with the results from literatures,two-dimensional unsteady model is validated.Moreover,the comparisons made in two-dimensional temperature field show that,for single-step reaction,the temperature gradient is larger and reaction zone is smaller,while for multi-step reaction,the temperature gradient is smaller and reaction zone is larger due to the difference of time scale,and the temperature field for multi-step reaction is in good agreement with the actual situations.

combustion model;premixed combustion;porous media;two-dimensional numerical simulation

2014-03-10

辽宁省高校优秀人才支持计划(LJQ2011135)；沈阳工程学院创新团队科技项目(LGTD-1202)

夏永放(1979-)，男，安徽界首人，讲师，博士，主要从事多孔介质燃烧技术、换热设备强化换热方面的研究.

TK16

A

1673-1603(2014)02-0118-05

(责任编辑张凯校对佟金锴)