基于自适应分形的射线图像增强算法

赵英亮，王黎明，韩 焱

（中北大学 电子测试技术国家重点实验室，太原 030051）

射线图像由于存在噪声、X曝光不当等原因易出现边缘模糊、对比度低等问题，易造成疵病及缺陷的漏判或误判。射线图像的主要特征是目标与目标之间、目标和背景之间没有显著的灰度变化，其灰度对比度不强，人眼对其的视觉分辨或机器识别较为困难，而且图像信息分布强弱不均往往会产生强信息淹没弱信息的现象。

现有的对比度增强技术，大都在增强对比度的同时，图像噪声也会增强。图像处理中的分形方法由于考虑的是图像整体和局部、大局部和小局部之间的统计自相似性，具有一定的抗噪能力。图像中每个像素点的分形维数值反映出该点灰度与周围点的相似度，不同的分形维值反映的是图像整体与局部的不规则性和差异性。因此可以把一副图像从灰度空间变换到分形维空间，利用图像各像素点的分形维数值作为加权值对原灰度图像进行增强。

1 传统的分形图像增强方法

Mandelbrot研究发现，描述自然界分形现象的最好的模型是分形布朗运动（FBM），其认为随机的运动是自然界产生不规则表面的结果。而随机的运动是自然界普遍存在的现象，因此图像也可认为是随机运动形成灰度不同的分形布朗运动的结果。各向同性的分数布朗随机场（FBR）是描述自然景物的有效方法之一，同一图像区域的灰度表面具有统计意义上的自相似性，这样可以用FBR来描述一副灰度图像了［1］。

1.1 分形布朗运动

离散分数布朗运动场模型是一种有效分形数学模型。分形理论认为图像表征了一个分数布朗运动（FBM）。设BH（u）为一分数布朗运动，u为某一点（ux，uy）的正向量。若存在 H，在0＜H＜1时，若对任意u和Δu都满足：

则称BH（u）为分数布朗随机场（FBR）［2］。其中 F（k）为与u，Δu无关的零均值的高斯随机变量的分布函数；Pr为概率测度；表示范数；H 为分形参数；r为增量值。

若BH，ΔBH取离散值，则称式（1）为离散布朗随机场（DFBR）。设图像区域的表面满足DFBR模型，则式（1）可以写作：

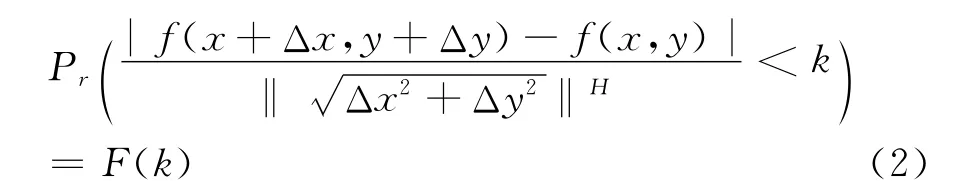
式中：f（x，y）为图像在点（x，y）处的灰度像素值。

通常一个分数布朗函数由零均值高斯增量的随机过程描述为［3］：

1.2 H参数及分形维数的提取

式（3）也可以被写为：

进一步推导为：

对两边取对数，能够得到表示式如下：

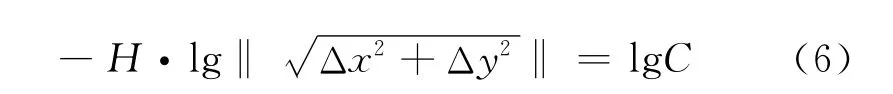
进一步推导为：

DFBM的分形维度D与它的Hurst指数H之间满足［4－5］：

式中：DT为图像表面的拓扑维数，对于平面图像它的值为2。

1.3 具体实现

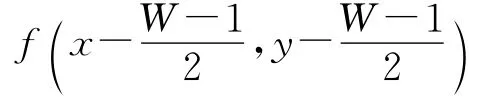
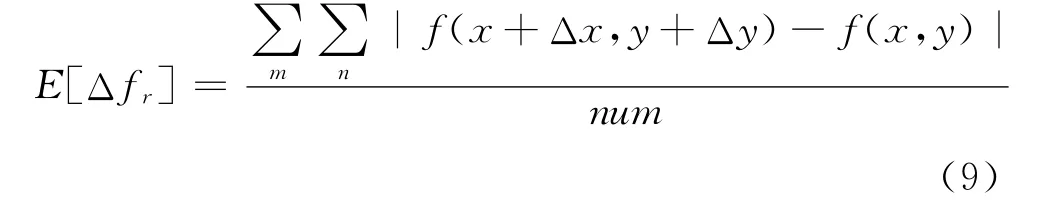
其中m∈x±W，n∈y±W，能够遍历滑动窗口22里除中心点外所有的像素点。num为满足距离为r的点的个数。

利用式 （7）与（8）即可求得H参数与分形维D。

仿真数据及处理结果见图1。原图为64×64的灰度图，采用大小为5×5的滑动窗口。背景灰度值为50，在第10列，20列，30列，40列，50列，60列各有一行灰度值为56，55，54，53，52，51的竖线。

从图1可以看出，6条灰度值相差很小的线，图6（b）～6（d）中的边缘检测算子与图6（e）中的小波算法均无法全部检测出所有的线来，而图6（f）中分形增强算法能够准确检测出6根线来。

1.4 存在问题

从图1会发现，图6（f）中的分形算法虽然能准确检测出目标结果，但其边缘会比原来的边缘要较宽，分析其原因，是因为第10列的像素值56导致周围范围为窗口宽度的H参数全部产生奇异。其它5条线（窗口宽度）也均是如此。另外如果原始图像中加噪声，则处理结果将会大大不同，因为此方法对灰度奇异值比较敏感，图2中为背景灰度值为150，第10列灰度值为10，第20列灰度值为20，依次递增，第60列为60。加噪后图像与利用上述分形增强算法处理的结果如图2。

图1 线条仿真图处理结果

图2 加噪后图像与分形增强处理结果

分析其原因，是因为其对像素点之间相似性判断比较敏感，所以对噪声也很敏感，所以需对其H参数进行修正。

2 自适应的分形增强方法

H参数的修正目的主要体现在两个方面，第一是边缘不应受周围灰度值的影响；第二就是去除噪声的影响。分析其原因，大都是因为一个或几个奇异点，造成周围的H参数出现异常，另外因工业图像中大多是检测目标或噪声，与普通生活中的图像所需增强的目标不同，因此根据周围点与中心点之间的差值关系，提出一种基于区域连通的H参数修正方法（与中心点的连通域）。

方法描述如下：

（1）首先对滑动窗口内处理图像从上到下、从左到右逐像素点进行扫描，计算该窗口中像素灰度值f（x，y）与中心像素灰度值f（x0，y0）的差值，根据差值绝对值大小和标准差关系来决定此点与中心点的连通关系。

（2）先判断是否有连通点（判断方法依据上条来决定），如没有，则不修正，否则进入下一步。

（3）从与中心点相距最近处开始检索，即像素灰度值f（x±1，y±1）与中心点灰度值f（x，y）进行相减；如其差值的绝对值小于T（T与标准差有关），则认为与中心点是连通区域，并进行该方向连通点的计数；如差值的绝对值不小于T，则停止该方向搜索。

（4）从有连通点的方向，继续沿各个方向搜索，如无连通点，则停止该方向搜索，并将计数中该方向点数减去，直到全部方向都遍历结束为止。

（5）如果该连通区域内的点的个数大于窗口内总点数的一半，则认为是背景，修正其H参数，否则如点数为0，则认为是噪声，修正H 参数以去除此点的影响，否则认为是奇异点（边缘），保留其H参数值。

对图2（a）进行上述修正后，修正后处理结果如图3所示。从图3中可以看出，其检测结果比较理想。

图3 自适应分形增强算法检测结果

仿真原始图像如图4（a）所示。考虑到实际成像中，如工业无损检测的试件存在两类缺陷形式，即线状缺陷（如裂纹）和面状缺陷（如气孔、缩松），因此在原始图像中制作了线状和面状图形元素。这两类形状也是其它图像中的基本构成，具有较为普遍的意义。图4（b）为受正向脉冲随机噪声污染的图像，为射线数字图像中的仿真图像；加噪图像的信噪比（SNR）为7.440 5dB，从图中可见受噪声污染较为严重。从图4（c）可见，3×3窗口中值滤波对图像细节有破坏作用，大于3×3的窗口对细节的破坏将更大。而该算法对噪声去除效果良好，且对图像细节具有较好的保护作用。

图4 仿真与滤波图像

图5（a）是使用透照电压220keV，管电流1.5mA，对厚度10mm的钢板进行数字成像的原始图像。图5（b）是利用上述方法处理的结果，图5（c）是图5（a）中横线所指行的灰度值，图5（d）是与5（b）中相同行的灰度值，可以看出处理结果比原图更能有效地提高分辨率。

3 结论

对于射线图像来说，其有用目标与背景之间灰度对比度不强，则对其进一步的识别较为困难。对于灰度图像来说，分数布朗运动所描述的是环绕某一点像值周围的像素点之间的关联性，对于图像窗口内灰度差别大，H 参数就越大，对于图像窗口内灰度差别小，H参数就越小，从这点出发，经过归一化处理后，即可有效调整图像中的灰度值。便使得增强后的图像既能保留图像中原有细节和边缘，又能突出视觉不易觉察的图像中的灰度差别。但是试验结果证明，分形进行图像增强时，在突出有用细节的同时，不可避免地对噪声也很敏感，因此笔者提出一种新的自适应方法，利用区域连通的特点来有效区分噪声信号与边缘信号，使得射线图像增强结果既具有高的分辨能力，又具有较好的抗噪性，并有良好的边缘特性。

图5 透度计图像及处理结果

［1］ STACH S，CYBO J.Multi－fractal description of fracture morphology［J］.Theoretical Basis. Materials Characterization，2003，51（3）：79－86.

［2］ LUO C H，GRAE LEE W M，LAI Y C，et al.Measuring the fractal dimension of diesel soot agglomerates by fractional brownian motion processor［J］.Atmospheric Environment，2005，39（2）：3565－3572.

［3］ Guy jumarie.Random time－dependent brownian motion a new approach to fractals of ordern［J］.Chaos，Solutions and Fractals，2002，14（6）：715－724.

［4］ BREWER J，DI L.Girolamo.Limitations of fractal dimension estimation algorithms with implications for cloud studies［J］.Atmospheric Research，2006，23（9）：201－228.

［5］ 李莉.基于分形维数和分形布朗运动的原木缺陷图像处理［D］.哈尔滨：东北林业大学，2007：42－45.