空间稳定系统壳体翻滚失准角误差精确补偿

何虔恩，高钟毓，吴秋平

（清华大学 精密仪器系，北京 100084）

空间稳定系统壳体翻滚失准角误差精确补偿

何虔恩，高钟毓，吴秋平

（清华大学 精密仪器系，北京 100084）

壳体翻滚是提高空间稳定系统长时间工作精度的技术手段之一，但其失准角误差将引起速度和姿态扰动。对该误差进行建模、标定与补偿是解决此问题的有效措施。在误差补偿时，由冗余角变化导致的交叉耦合影响对长航时高精度惯导系统是不能忽视的。根据壳体翻滚失准角误差矢量的几何投影关系，建立物理平台坐标系（P系）与陀螺三面体坐标系（G系）之间的坐标转换关系，分析冗余角变化引入的交叉耦合影响，并进行计算机仿真和实际试验。结果表明：冗余角使P系相对G系沿z向的角运动附加极轴壳体翻滚周期分量，其幅值为失准角与冗余角正切函数的乘积；误差补偿考虑这一项，东速、横摇和航向精度十天可提高30%~50%。

空间稳定系统；壳体翻滚失准角；误差补偿；冗余角；交叉耦合

采用旋转调制技术，可在无外部参考信息条件下，自动地补偿惯性仪表固有误差，因而能有效提高惯性测量组合和由其组成的惯性导航系统的精度[1-2]，在平台式和捷联式惯性导航系统中获到广泛应用[3-4]。旋转调制技术主要有壳体翻滚和台体翻滚两种实现方式，目的都在于平均与壳体或与台体有关的误差[5]。然而，任何技术都有两面性，旋转调制也有其缺陷[6]，例如，由于壳体翻滚轴不可能恰好安装到与顶端光电传感器零位一致，即不可避免地存在壳体翻滚失准角误差，在壳体翻滚条件下，惯性导航系统的速度和姿态将出现不可忽视的扰动分量[7]。进行壳体翻滚失准角误差的建模、标定与补偿是解决这一问题的有效措施。

高钟毓[3]通过几何投影关系直观地进行了壳体翻滚失准误差的建模。在此基础上，胡佩达等分别基于静止水平基座条件下的框架信息[8]和扰动比力[7]研究了适用于静态和动态环境的壳体翻滚失准误差标定与补偿方法。然而，已有研究在补偿时没有考虑极轴和赤道陀螺动量矩矢量不正交度（由冗余角大小表征）的变化引入的交叉耦合影响，因而未能精确地扣除壳体翻滚失准角误差，主要表现为：速度和姿态中壳体翻滚周期扰动分量的幅值随着冗余角变化量的增加而增大。

针对上述问题，在给出P系、G系、赤道陀螺坐标系（G2系）、壳体翻滚角和失准角等定义的基础上，根据壳体翻滚失准角误差矢量的几何投影关系以及框架伺服系统驱动平台跟踪陀螺的工作原理，建立P系与G系之间的坐标转换关系，进而分析出冗余角变化引入的交叉耦合影响。最后，对所述理论进行计算机仿真和实际试验验证。

1 相关坐标系及物理量定义

1.1 G系与G2系

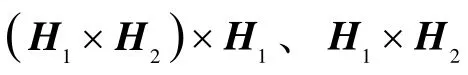
根据上述定义知，G系相对惯性系（i系）的漂移角速度取决于两个陀螺的漂移角速度，其中，x和 y向漂移取决于极轴陀螺漂移，即

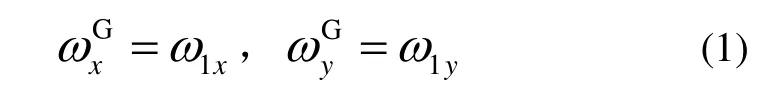
式中ω1x和ω1y分别表示极轴陀螺相对i系沿xG和yG方向的漂移角速率。G系的z向漂移需通过以下过程求解：

根据角速度加法原理，有

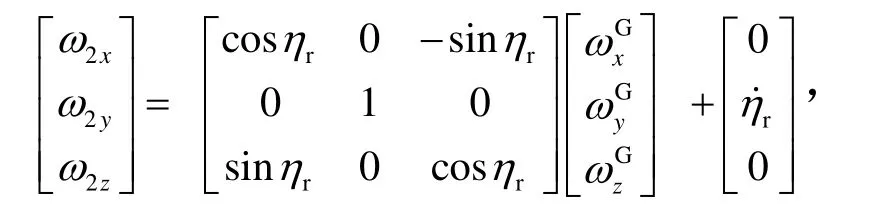
其中，ω2x、ω2y和ω2z分别表示赤道陀螺相对i系沿xG2、yG2和zG2方向的漂移角速率，因而有：

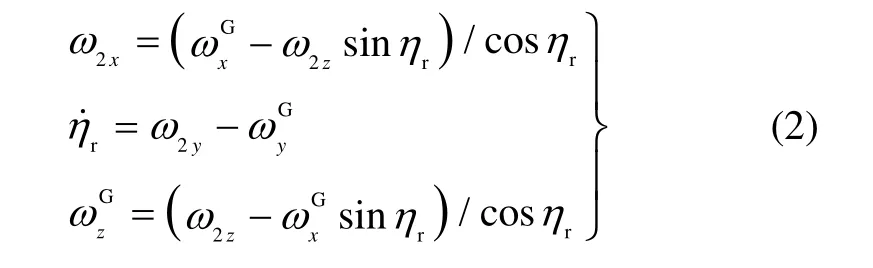
至此，得到了G系漂移角速度和冗余角速率与陀螺漂移之间的关系。由式(1)和(2)可见，由于冗余角ηr的存在，极轴陀螺x向漂移将耦合到G系的z向漂移中；赤道陀螺z向漂移将耦合到G2系的x向漂移中，而G系的x和y向漂移则不存在耦合分量。

1.2 P系与G系

P系在框架系统的伺服作用下跟踪G系运动，忽略跟踪误差和极轴陀螺安装误差，从P系按如下路径旋转到G系：

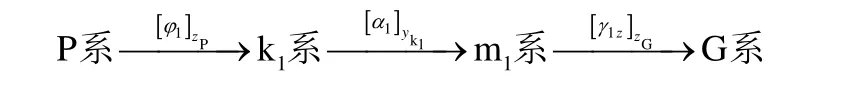
1.3 P系与G2系

赤道陀螺通过冗余环间接安装在物理平台上。忽略冗余轴和赤道陀螺的安装误差，从P系按如下路径旋转到G2系：

其中，α2和φ2分别为赤道陀螺的壳体翻滚失准角和壳体翻滚角；Yr为冗余轴转角； γ2x与极轴和赤道陀螺的壳体翻滚角与失准角有关，将在下文给出其具体表达式。

2 壳体翻滚失准角误差的精确补偿公式

2.1 G系与P系的坐标转换关系

假设壳体翻滚失准角为小角度，则根据第1节的定义，可得壳体翻滚失准角误差矢量的几何投影如图 1所示。

图 1 壳体翻滚失准角误差矢量的几何投影示意图Fig. 1 Geometric projection of case rolling non-alignment angle error vectors

由图 1可直观地看出，在壳体翻滚条件下：

1）为使极轴陀螺（本体直接安装在平台上）输出信号保持为零，框架伺服系统应驱使P系沿xG和yG运动，以分别抵消如下分量：

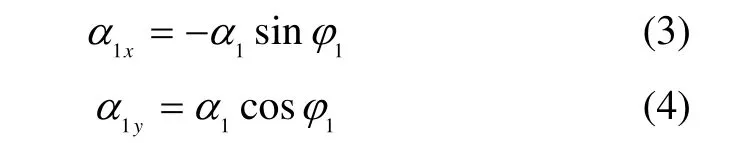
2）为使赤道陀螺（本体安装在冗余环上，冗余环通过冗余轴安装在平台上）输出信号保持为零，框架伺服系统应驱使P系沿zG运动，并驱使冗余轴转动，以分别抵消如下分量：

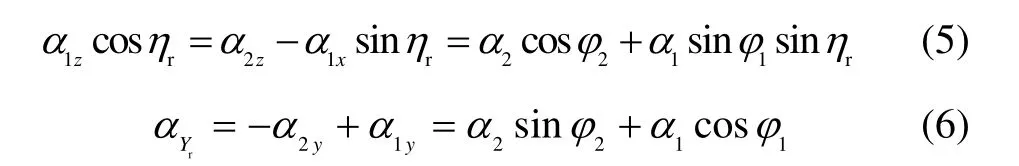
综上可得，P系到G系的坐标转换矩阵：

以及冗余轴转角：

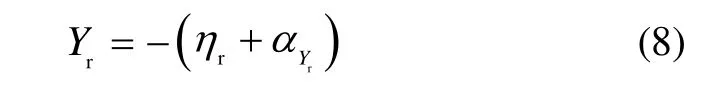
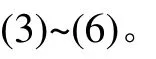
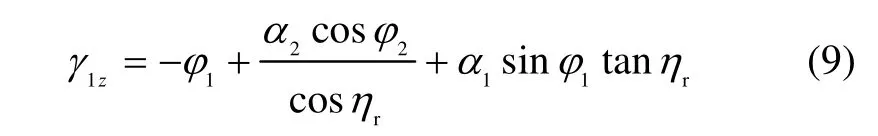
同理，有

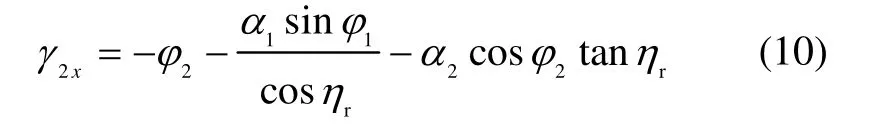
2.2 分析与讨论

至此，得到壳体翻滚失准角为小角度并忽略其二阶小量和框架伺服系统跟踪误差的情况下，G系与P系的坐标转换关系（见(7)）以及冗余轴转角（见式(8)）表达式。可见，G系与P系之间的Euler小角矢量有如下特点：

1）沿x轴和y轴方向的分量取决于极轴陀螺的壳体翻滚失准角和壳体翻滚角；

2）沿z轴方向的分量一部分取决于赤道陀螺的壳体翻滚失准角和壳体翻滚角，另一部分则取决于极轴陀螺壳体翻滚失准角、壳体翻滚角和冗余角正切；

3）在壳体翻滚条件下，壳体翻滚失准角主要引起Euler小角矢量中同等量级的壳体翻滚周期分量。然而，当冗余角相对初始值ηr0（壳体翻滚失准角标定结束时刻的值）发生变化时，P系相对G系沿z向的运动将附加如下分量：

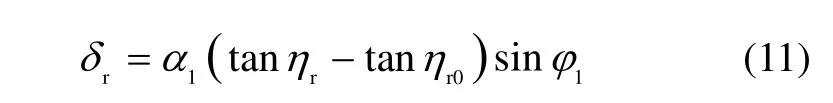
取ηr0=0，α1=10'，可得这一分量的幅值与冗余角的关系如表 1的第二行所示。

表 1 冗余角变化引入的交叉耦合分量（ηr0=0，α1=10'）Tab.1 Cross coupling items due to redundancy angle variation

根据壳体翻滚失准角误差传播特性的分析结果可知，δr将引起东向速度误差中幅值约

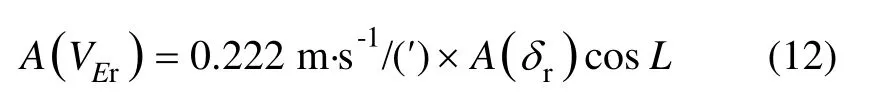
的壳体翻滚周期分量，这里，L为当地纬度， A(δr)表示 δr的幅值。这一分量的幅值与前述冗余角的关系如表 1的第三行所示。同时，还将导致航向角误差和横摇角误差中幅值分别为

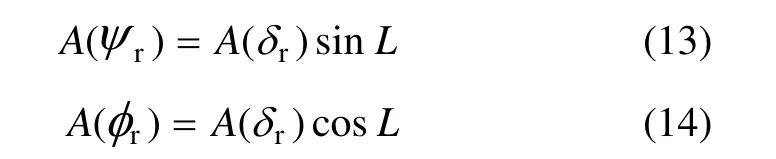
的壳体翻滚周期分量，其量级与前述冗余角的关系见表 1的第二行。易见，随着冗余角变化量的增加，δr引起的东向速度、航向角和横摇角误差中壳体翻滚周期扰动分量的幅值呈增大趋势，这对于长航时高精度的惯导系统而言是不容忽视的。

以上讨论表明，减小冗余角相对初始值的变化量和极轴陀螺壳体翻滚失准角或采用模型进行壳体翻滚失准角误差精确补偿均可有效降低上述导航误差。减小壳体翻滚失准角和冗余角的变化是有限的，而采用模型进行误差精确补偿则为较简捷、有效的措施。

3 计算机仿真与试验结果

3.1 仿真设置

首先，生成空间稳定系统仿真数据——框架角、比力和壳体翻滚角，其中，纬度设定为 L=40°；极轴和赤道壳体翻滚失准角均设为4'，翻滚周期为8 min；冗余角平均变化率设为0.01 (°)/h。其次，利用系统仿真数据进行初始对准与标定及导航解算，壳体翻滚失准角误差补偿分别采用不考虑冗余角变化和考虑冗余角变化两种补偿模型（模型A和模型B）。

3.2 仿真结果

在导航第一天，两种模型对应的导航结果无显著差异；在导航第十天，模型A对应的东向速度、航向角和横摇角误差中8 min周期分量的幅值分别达到了0.03 m/s、0.13'和0.16'，而模型B对应的结果则接近0。这分别与按前述理论进行分析所得的如下结果相一致：

1）东向速度0.222 ×0.4 ×0.01 ×240 × 0.175 × cos40 °≈ 0.03m/s ；

2）航向角0.4 × 0.01 ×240 × 0.175 × sin40 °≈ 0.11′；

3）横摇角0.4 × 0.01 × 240 × 0.175 × cos40 °≈ 0.13′.

3.3 试验结果

2013年4月，某空间稳定系统在纬度40°进行了十余天的静态导航试验。利用该组试验数据进行初始对准与标定及导航解算，壳体翻滚失准角误差补偿分别采用第3.1节中的模型A和模型B。图2～图4分别摘录了两种情况下导航第十天附近的东向速度、航向角和横摇角误差曲线（在导航第一天，两种情况的差异不显著；结果进行了归一化处理）。

由图2～图4易见，采用模型B进行壳体翻滚失准角误差补偿后，导航第十天东向速度、航向角和横摇角误差中 8 min周期分量幅值比模型 A减小了30%～50%。根据初始对准与标定期间得到的冗余角平均变化率和壳体翻滚失准角参数，按前述理论进行分析，得到的结果与以上试验结果相吻合。

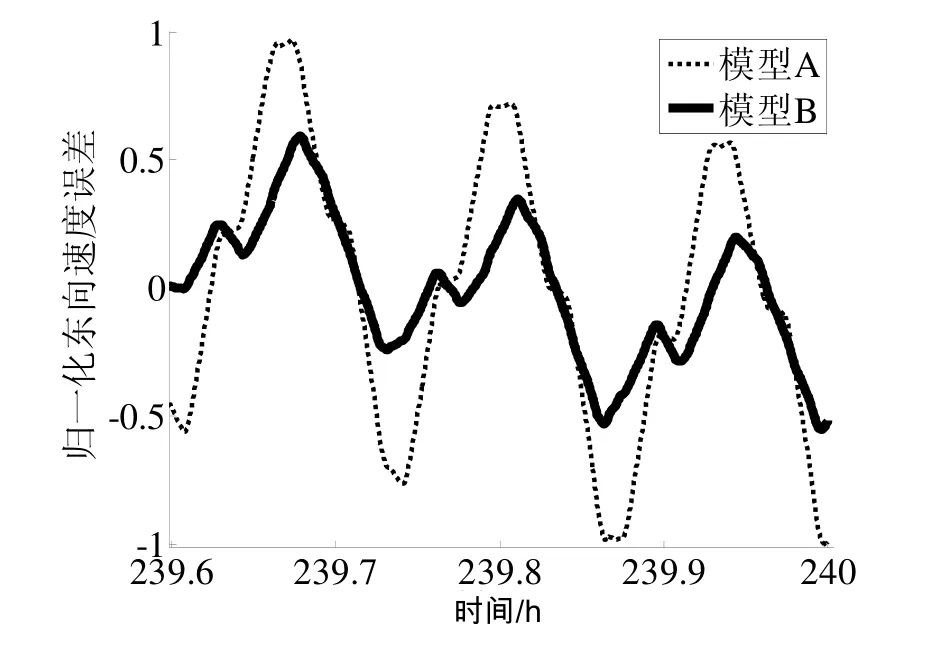
图 2 考虑冗余角影响前/后（模型A/B）东向速度误差曲线Fig.2 East velocity errors test results for cases of neglecting/ considering the influence of cross coupling effect (Model A/B)

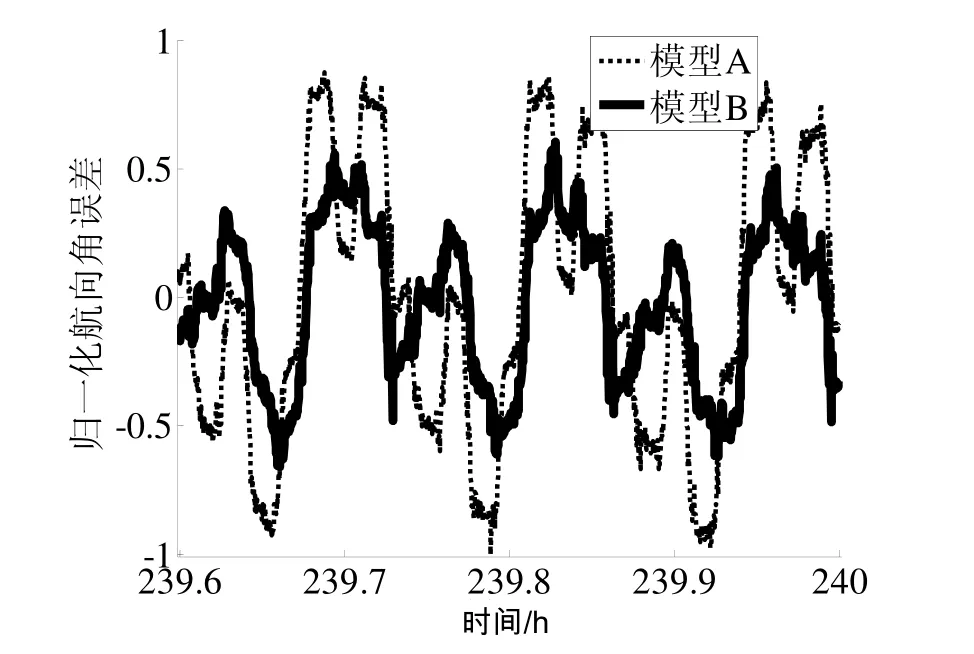
图 3 考虑冗余角影响前/后（模型A/B）航向角误差曲线Fig.3 Yaw errors test results for cases of neglecting/ considering the influence of cross coupling effect (Model A/B)

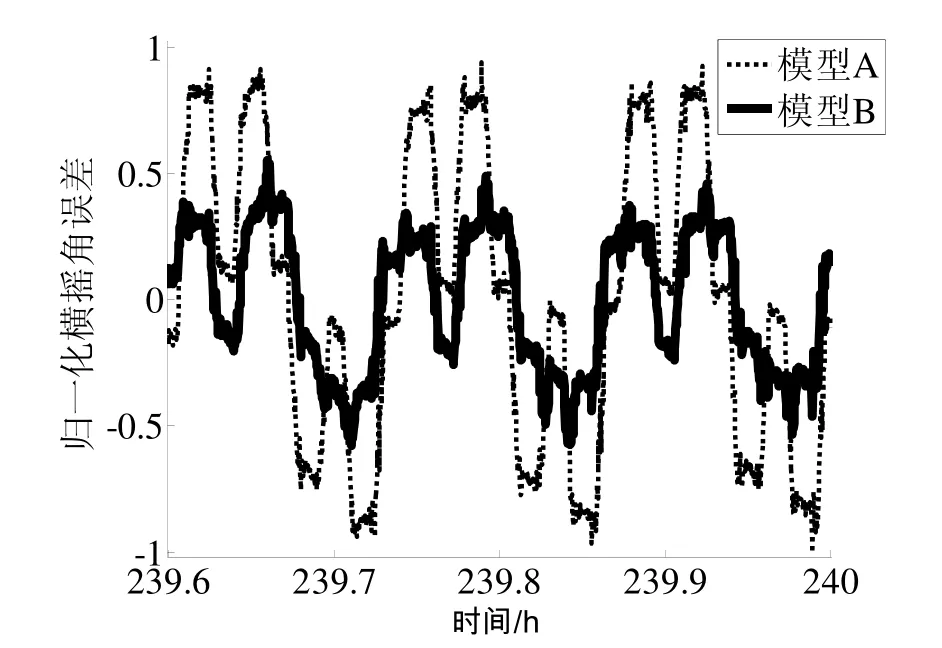
图 4 考虑冗余角影响前/后（模型A/B）横摇角误差曲线Fig.4 Roll errors test results for cases of neglecting/ considering the influence of cross coupling effect (Model A/B)

另外，模型B对应的误差中仍残留一定幅值的壳体翻滚扰动分量，其原因在于实际壳体翻滚轴存在回转误差，使失准角随壳体翻滚至不同位置而发生一定幅度的变化，而这与轴系的机械稳定性、顶端光电传感器光学特性以及伺服跟踪误差等因素息息相关。

4 结 论

对壳体翻滚失准角误差进行建模、标定和补偿是解决由壳体翻滚造成的惯导系统速度和姿态扰动问题的有效措施。针对速度和姿态中壳体翻滚周期扰动分量的幅值随冗余角变化量增加而增长的问题，根据壳体翻滚失准角误差矢量的几何投影关系以及框架伺服系统驱动平台跟踪陀螺的工作原理，建立P系与G系之间的坐标转换关系，并分析冗余角变化引入的交叉耦合影响。理论、仿真和实际试验均表明：采用考虑冗余角变化的模型进行壳体翻滚失准角误差补偿之后，东向速度、横摇角和航向误差中壳体翻滚周期分量的幅值十天可减小30%～50%，具有工程应用价值；所述理论对系统硬件设计具有指导意义。

（

）：

[1] Wang X, Wu J, Xu T, et al. Analysis and verification of rotation modulation effects on inertial navigation system based on MEMS sensors[J]. Journal of Navigation, 2013, 66(5): 751-772.

[2] Nie Q, Gao X Y, Liu Z. Research on accuracy improvement of INS with continuous rotation[C]//International Conference on Information and Automation. 2009: 870-874.

[3] 高钟毓. 惯性导航系统技术[M]. 北京：清华大学出版社，2012：321-322.

[4] 张和杰，常国宾. 旋转调制式捷联惯导误差分析[J]. 海军工程大学学报，2011，23(5)：55-59.

ZHANG H J, CHANG G B. Error analysis of rotation modulating strapdown inertial navigation system[J]. Journal of Naval University of Engineering, 2011, 23(5): 55-59.

[5] Ben Y Y, Yang X L, Wu X, et al. The restrain theory of gyro constant error with rotation modulation[J]. Advanced Materials Research, 2012, 566: 313-316.

[6] Zhou Y, Deng Z H, Wang B, et al. Moving base disturbance suppression method of rotary INS based on rotation angular rate[C]//2013 9th Asian Control Conference. IEEE, New York, 2013: 1-5.

[7] 胡佩达，高钟毓，吴秋平，等. 基于扰动比力的壳体翻滚失准角辨识[J]. 清华大学学报(自然科学版)，2010，50(9)：1472-1475.

HU P D, GAO Z Y, WU Q P, et al. Identification of misalignment angles of a gyro case rotation axis based on disturbed specific forces[J]. Journal of Tsinghua University(Science and Technology), 2010, 50(9): 1472-1475.

[8] 胡佩达，高钟毓，吴秋平，等. 壳体翻滚失准角模型最小二乘辨识方法[J]. 中国惯性技术学报，2009，17(4)：393-396.

HU P D, GAO Z Y, WU Q P, et al. Least squares method identification of the error angle of case rotation axis[J]. Journal of Chinese Inertial Technology, 2009, 17(4): 393-396.

Accurate compensation for case rolling misalignment angle in space-stable systems

HE Qian-en, GAO Zhong-yu, WU Qiu-ping
(Department of Precision Instruments, Tsinghua University, Beijing 100084, China)

While Case rolling is one of the techniques for improving long term accuracy of space-stable systems, its non-alignment errors would cause velocity and attitude disturbances. Modeling, calibrating and compensating the non-alignments is an effective solution. Cross coupling effect due to redundancy angle variation should be considered in compensating high-accuracy long-time inertial navigation systems. In this paper, the coordinate transformation between physical platform frame (P frame) and tri-axial gyroscope frame (G frame) is established based on the geometric projection of case rolling non-alignment angle error vectors, and the cross coupling effect is analyzed. Simulation and test results show that, due to redundancy angle, there exist periodic components of polar case rolling in z-axis angular motion of P frame with respect to G frame, whose amplitude equals the product of non-alignment angle and tangent of redundancy angle. The errors of east velocity, roll and yaw can be reduced by 30%-50% in ten days with the proposed error compensation model.

space-stable systems; case rolling non-alignment angles; error compensation; redundancy angle; cross coupling effect

联 系 人：高钟毓（1936—），男，教授，博士生导师。E-mail∶ gaozy@mail.tsinghua.edu.cn

1005-6734(2014)05-0572-04

10.13695/j.cnki.12-1222/o3.2014.05.003

U666.1

A

2014-05-22；

2014-08-26

总装“十二五”预研项目（51309030401）

何虔恩（1985—），男，博士后，研究方向为导航系统与控制。E-mail：heqianen2005@126.com