DIWO-SVM在除尘风机故障诊断中的应用

蔡 鑫 南新元 孔 军，2

（新疆大学电气工程学院1，新疆 乌鲁木齐 830047；江南大学物联网工程学院2，江苏 无锡 214122）

DIWO-SVM在除尘风机故障诊断中的应用

蔡 鑫1南新元1孔 军1，2

（新疆大学电气工程学院1，新疆 乌鲁木齐 830047；江南大学物联网工程学院2，江苏 无锡 214122）

冶金除尘风机广泛应用于冶金工业中，如果能及时检测诊断出除尘风机的故障，就能够很好地提高风机的安全性。针对除尘风机故障，提出一种基于差分入侵杂草算法优化支持向量机（DIWO-SVM）的模型。差分入侵杂草算法（DIWO）是一种具有较强鲁棒性、自适应性和随机性等特点的数值优化算法，用于支持向量机（SVM）的参数优化，能有效提高SVM分类准确率，以准确地识别除尘风机常见的故障。通过比较，验证了这种算法是可行的，并且具有很好的诊断能力。

除尘风机 支持向量机 差分进化 故障诊断 数值优化

0 引言

冶金除尘风机是冶金生产系统的关键设备，长期工作于高温、高湿、高粉尘环境，工作强度大，易产生磨损等各类故障。为了了解风机状况和故障类别，对设备故障提前预警并作出诊断，需对风机进行监测。一般情况下采集旋转机械的振动信号作为原始依据。由于旋转机械的振动具有多个环节的振动，并且冲击、振动相互影响，因此采集到的振动信号是具有很大干扰噪声的复杂信号，对风机进行故障诊断非常困难［1］。

近年来，人工智能方法如神经网络、模糊理论和遗传算法等在故障诊断中得到广泛应用，这些方法能够处理传统故障诊断方法无法解决的问题［2－3］。但是，在实际应用中，由于能得到的故障数据样本数量有限，使得一些方法的应用受到了很大的限制，选用合适的分类器用于设备状态识别显得非常必要。

在统计学理论的基础上，Vapnik提出了支持向量机（support vectormachine，SVM）算法。该算法对小样本条件下的非线性映射具有优势，又能限制过学习，特别适合于小样本集的数据处理，在故障诊断方面显示了其优越性。朱新才、邓星等提出的二叉树支持向量机实现了训练样本完全可分［4］；吕蓬提出的改进最小二乘支持向量机，提高了故障分类的精度［5］。但是，因为支持向量机参数选择的合理性直接决定分类精度，所以，SVM分类模型参数存在优化选取的问题。入侵杂草优化（invasive weed optimization，IWO）算法［6］，是由Mehrabian等提出的一种模拟自然界杂草生长过程的随机搜索方法，具有鲁棒性强、易于理解和易于实现等特点。本文采用差分入侵杂草（differential invasive weed optimization，DIWO）算法优化SVM分类模型的参数，以冶金除尘风机滚动轴承振动信号的特征参数为训练对象，用于除尘风机旋转机械故障诊断。诊断结果表明，本文提出的方法与传统的SVM和GA-SVM相比，有很好的诊断效果。

1 支持向量机（SVM）

20世纪90年代，由Vapnik提出的支持向量机成功地解决了高维问题和局部极值问题［7］。近年来，其以良好的理论基础和应用效果，逐渐成为故障诊断的研究热点。

SVM不仅可以解决线性问题，而且可以解决非线性问题。将输入样本x通过一个非线性映射φ映射到一个高维的特征空间L中，使在特征空间中可以应用线性支持向量机的方法解决样本空间中的高度非线性分类问题。最优化问题的表达式如下［8］：

特征空间中的分类约束条件为：

式中：C＞0为惩罚因子，它控制对错分样本的惩罚的程度；ξi≥0为松弛因子。

式（3）为在不等式约束下的一个二次规划问题。根据Mercer条件，可以用核函数K（xi，xj）=φ（xi）T× φ（xj）将非线性支持向量机转化为目标函数，即转化为下式所示的一个二次规划问题。

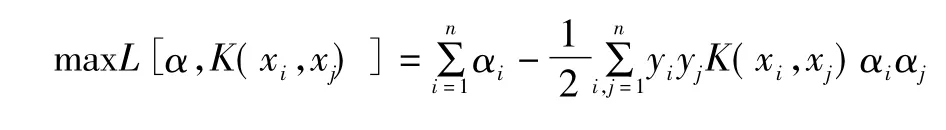
2 DIWO算法

IWO算法只是随机地初始化个体，再以一定范围内的随机步长产生新个体，进而选取适应度好的个体，如此反复进行直到满足结束条件。差分进化具有较强的搜索能力、良好的鲁棒性和收敛性。将差分进化算法与杂草算法有机结合，可使杂草“有目的”地向当代较好个体“移动”，弥补了杂草算法不能很好应对高度耦合问题的不足，保证了种群个体的多样性，提高了寻优精度和寻优速度。

2.1 初始化

将一定数量的可行解随机分布在整个搜索空间（D维）中。第t次迭代的种群定义为Xt={X1，t，X2，t，…，Xm，t}。

2.2 繁殖

种群Xt中的每个杂草可以在以它为中心的区域内产生种子。Xi，t（i∈［1，m］）可以根据其适应性（繁殖能力）产生不同数量的种子，由Xi，t（i∈［1，m］）产生的种子个数为：

式中：smax表示一个杂草所能产生的种子的最大值；f（Xt）为当前杂草的适应度值；Fmax和Fmin分别为当前种群中杂草对应的最大和最小适应度值。

2.3 空间扩散

在IWO中，以父代为轴线，子代个体以均值为0、标准差为σ扩散在D维空间中。每次迭代过程中，种群中所有杂草的σt都是相同的。这样，种群中所有父代产生的子代都以相同的方式分布在其周围。种群多样性降低，靠近全局最优的一些杂草往往容易陷入局部最优。为了解决这样的问题，每次迭代都根据杂草相应的适应度值调整其个体的标准差。

任一杂草在靠近期望全局最优的过程中，要求在搜索空间内其种子的分布应该是下降的，以免错过实际最优位置。相比之下，对于适应度值低的杂草，其种子需要更多的分布才能在搜索空间寻找到其他期望域。在此情况下，每次迭代中所有杂草的标准差σi，t是不一样的，从而保证了种群的多样性。

式中：σt为第t次迭代的标准差值；σmax和σmin分别为最大标准差值和最小标准差值；n_m_i为非线性调和指数；tmax为最大迭代次数；Fmedian，t、Fworst，t和 Fbest，t分别为当前种群杂草对应的中间、最差和最好适应度值。

当杂草的适应度值小于Fmedian，t时，其子代的适应度值σi，t将小于 σt；而具有较大适应度值的杂草，其子代的适应度值 σi，t将高于 σt。这样，根据标准差σi，t，每个杂草种子Xi，t可以得到si个子代种子。子代和父代形成一个新的具有n维的中间种群Vt。其中的每个种子Vi，t（i∈［1，n］）行变异、交叉产生另一个种群Zt。

2.4 基于差分进化的局部选择

Z，Zt中的每一个种子与其相应的父代Vt相比，选择适应性更强的子代构成一个具有n个杂草的种群P。这样，在种群P中的每个杂草可以描述为：

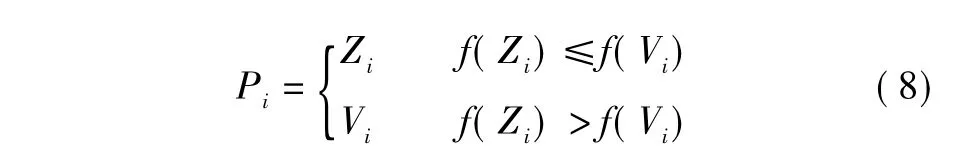
2.5 最终选择

种群P中的个体按照适应度值大小排序，选取适应度好的前m个个体，淘汰其余的个体。重复2.2～2.4所述操作，直到满足设定的最优解条件或者达到最大迭代次数。

3 DIWO-SVM故障诊断

不同于神经网络基于经验最小化的原则，SVM是基于结构风险最小化原则。SVM通过引入具有特殊性质的核函数，将实际问题通过非线性变换转换到高维的特征空间，在高维空间中构造线性决策函数，实现原空间中的非线性决策函数，使得求解支持SVM的过程只与训练样本的数目有关，而与样本的维数无关［8－9］。

3.1 核函数的选取

核函数是SVM的关键部分，其中的参数在SVM的训练和诊断过程中起着重要的作用。局部核函数学习能力强、泛化性能弱，而全局核函数泛化性能强、学习能力弱［10］。本文选择混合核函数作为SVM的核函数。混合核函数由全局多项式核和局部高斯核线性组合而成，二者优势互补，以提高支持向量机模型的精度。

局部核函数选择的是径向基函数（RBF），全局核函数选择的是多项式核函数［11］。构造的混合核函数为：式中：q为多项式核阶数；a∈［0，1］为混合权重系数。当a=0时，混合核函数为RBF核函数；当a=1时，混合核函数为多项式核函数。

3.2 DIWO-SVM算法

DIWO优化SVM的过程如图1所示。

为了得到更好的故障诊断结果，本文提出了一种将DIWO和SVM相结合的算法，即DIWO-SVM。利用DIWO算法优化SVM中RBF核函数参数σ、惩罚因子C、多项式核函数参数q以及混合权重系数a，再用已训练的SVM进行故障诊断。

DIWO-SVM故障诊断流程如下。

①获得故障数据。在给风机一定输入的情况下，对故障进行测试，系统响应经采样得到测试数据，选择其中的一部分作为SVM的故障集。所有的采样数据都应该归一化处理，经小波包分析得到故障特征向量。将这些故障特征向量分成两部分，一部分作为训练样本，另一部分作为测试样本。

②训练和测试。根据DIWO-SVM原理，对训练样本进行训练，得到优化决策函数。然后用测试样本进行测试，得到诊断的准确率。

③初始化。对杂草种群初始化，参数设置如下：初始种群数m=6，非线性调和系数n_m_i=2，种子突变率F=0.7，交叉率pcr=0.7，最大迭代次数tmax= 100，最大种群数Pmax=40。

④繁殖和更新。父代杂草通过突变、交叉繁殖后，根据适应度值大小排序，淘汰多余个体，更新种群。

⑤终止条件。若满足终止条件，则将种群中全局最优个体映射为（σ，C）和（q，a），并以此最优结果作为DIWO-SVM诊断模型的结构参数。

⑥利用DIWO算法优化核函数的参数。根据DIWO算法的原理，优化DIWO-SVM中的参数（C，σ）、（q，a）。用诊断的准确率作为DIWO算法的适应度函数。重复步骤②和⑥，直到满足结束条件。然后利用已优化、训练的SVM得到风机的故障诊断结果。

风机故障诊断过程如图2所示。

图2 故障诊断过程Fig.2 The fault diagnosis process

4 基于小波包能量故障特征提取

小波包分析是从小波分析中延伸出来的一种对信号进行更加细致的分解和重构方法［12］，由于所检测到的振动信号是非平稳的信号，利用小波包分解的多分辨分析思想能将信号分解到不同频带内进行处理。小波包分析不仅具备同时对信号低频、高频进行分解的能力，而且它将频率进行多层划分，根据信号特征自适应地选取频带，极大提高了频域分辨率。此外，它可以提取出信号能量作为输入向量。具体实现步骤如下。

①对现有的故障数据进行N层小波包分解，并且提取i层从低频到高频2N个频带的信号特征。

②对小波包分解系数进行重构，提取第N层各频带范围的信号。

③设EN为信号的第M层部分dN的能量，根据小波分析能量概念，则有：

式中：dM（k）为第M层高频部分的第k个幅值。

④构造特征向量。以能量组成特征向量，即特征向量T构造为T=［E1，E2，…，Ej］。然后对数据进行归一化，使所有的特征向量归一化到［0，1］区间。

当设备出现故障时，会对各频带内信号的能量有较大的影响。因此，用小波包分解重构后，各频带“能量”为风机转子故障信号的特征向量，可有效提取故障特征，从而为风机故障智能诊断提供了一种便捷的处理方法。

5 故障诊断试验

5.1 振动数据采集

本文的振动数据来自于某金矿1号高炉除尘风机轴承振动数据集，其电机转速为998 r/min，转轴的振动信号是采用安装在电机和风机转子负荷端轴座上的加速度传感器来获取的，共测得5种故障的数据文件。

总文件数、训练样本数和测试样本数如表1所示。

表1 数据样本Tab.1 数据样本

为了保证试验结果的准确性，将总数文件的70％作为训练数据文件，将30％的数据文件作为测试文件。将这些数据文件通过数据处理后得到的特征值作为训练样本和测试样本。

5.2 诊断结果

本试验研究的是5种故障类型，采用“一对多组合”的支持向量机进行分类。根据一对多组合分类思想，为每一种故障类型构造一个SVM，故障诊断的SVM模型如图3所示。SVM1用来识别正常（1）和异常（－1）；如果异常，再用SVM2来识别转子不平衡和其他异常；如果是其他异常，用SVM3来识别转子不对中和其他异常；SVM4用来识别转子弯曲和其他两类异常；SVM5用来识别转子松动和转子轴承裂缝。

图3 故障诊断SVM模型Fig.3 SVM model of fault diagnosis

经过仿真试验，得到其各种故障类型的实际分类和经DIWO-SVM的预测分类，如表2所示。

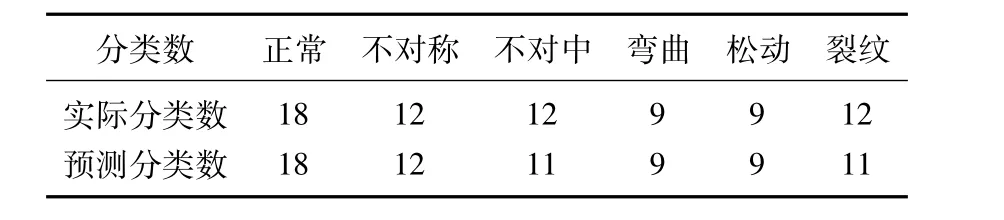
表2 故障实际分类与预测分类Tab.2 Real and predictive fault classifications

采用SVM［8］、GA-SVM［13］算法分别对冶金风机的故障进行诊断，并和本文提出的DIWO-SVM进行研究对比，结果如表3所示。由表3可知，DIWO-SVM的诊断精度最高。

表3 故障诊断情况Tab.3 The fault diagnosis situations

6 结束语

支持向量机对冶金风机的故障诊断提供了有效的解决方法。作为SVM重要的一部分，核函数参数优化对SVM的特性有极大的影响。本文提出的DIWO优化SVM，与传统的SVM、GA-SVM相比，分类性能好，诊断精度高，诊断时间短，可识别风机转子的不同状态，对冶金风机故障诊断具有很强的实际应用价值，为风机智能诊断提供了一种新的途径。

［1］董华，苏海涛.基于SVM的旋转机械故障诊断方法研究［J］.仪器仪表学报，2007，28（4）：175－197.

［2］杨超，王志伟.基于小波分析和模糊神经网络的齿轮故障诊断研究［J］.噪声与振动控制，2010，30（4）：64－67.

［3］Rama Rao K，Ariff YahyaM.Neuralnetworksapplied for faultdiagnosis of ACmotors［C］//Proceedings of the Information Technology，ITSim 2008 International Symposium on，2008：1－6.

［4］朱新才，邓星，周雄，等.二叉树支持向量机的旋转机械故障诊断［J］.重庆大学学报，2013，36（7）：21－26.

［5］吕蓬.旋转机械故障模式识别方法研究［D］.北京：华北电力大学，2010.

［6］ Mehrabian A R，Lucas C.A novel numerical optimization algorithm inspired from weed colonization［J］.Ecological Informatics，2006，1（4）：355－366.

［7］戴洪德，陈明，李娟.基于多层子支持向量机的多传感器故障诊断［J］.仪器仪表学报，2006，27（6）：1737－1739.

［8］翟永杰.基于支持向量机的故障智能诊断方法研究［D］.北京：华北电力大学，2004.

［9］邵小健.支持向量机中若干优化算法研究［D］.青岛：山东科技大学，2005.

［10］周金明，王传玉，何帮强.基于混合核函数FOA_LSSVM的预测模型［J］.计算机工程与应用，2013，10.3778/j.issn.1002－8331.1303－0459.

［11］Keerthi SS，Lin C J.Asymptotic behaviors of support vectormachines with Gaussian kernel［J］.Neural Computation，2003，15（7）：1667－1689.

［12］胡昌华，李国华，周涛.基于MATLAB 7.X的系统分析与设计——小波分析［M］.西安：西安电子科技大学出版社，2008.

［13］王凯，张永祥，李军.遗传算法和支持向量机在机械故障诊断中的应用研究［J］.机械强度，2008，30（3）：349－353.

Application of DIWO-SVM Approach in Fault Diagnosis of Dust Removal Air Blower

Themetallurgical dust removal air blowers are widely applied in metallurgical industry.To ensure the operation security of air blower，it is necessary to detect and diagnose the faults of the air blower timely.Aiming at the faults of the air blower，the model based on differential invasive weed optimization support vector machine（DIWO-SVM）is proposed.The DIWO algorithm is a numerical optimization algorithm which features strong robustness，good adaptability and stochastic performance；it is used to optimize the parametersof SVM，thus the classification accuracy of SVM can be effectively enhanced，to precisely identify the common faults of the dust removal air blower.The comparison verifies the feasibility and perfect diagnosis capability of this algorithm.

Dust removal fan Support vectormachine（SVM） Differential evolution Fault diagnosis Numerical optimization

TF181；TP277

A

新疆省自然科学基金资助项目（编号：2012211A004）。

修改稿收到日期：2014－01－21。

蔡鑫（1989－），女，现为新疆大学控制理论与控制工程专业在读硕士研究生；主要从事工业控制优化方面的研究。