探究式拉格朗日中值定理的论证
秦玉琨 赵雪华

【摘要】拉格朗日中值定理也称微分中值定理,在高等数学中占有重要地位.本文主要是利用探究法借助绘图软件观察总结得出拉格朗日中值定理的结论,进而论证该定理.
【关键词】拉格朗日中值定理;探究式;绘图软件
拉格朗日中值定理是微分学中的重要定理,它与罗尔定理、柯西中值定理统称为微分中值定理.内容上,它是罗尔定理的推广,也是联系函数与导数的桥梁.该定理的应用不仅在高等数学方面,它还广泛地应用于多个学科领域中,如数论、群论、流体力学等.拉格朗日中值定理是理工科院校高等数学课程中的重要内容,也是一个重点、难点内容.重点是因为它是微分学的理论基础,在进行一些公式推导与定理证明中都有很多应用;难点在于定理结论的得出以及推导论证的方法,学生不容易理解掌握.基于这种情况,本文提出了与传统教学法不同的探究式教学法讲解学习拉格朗日中值定理.
一、拉格朗日中值定理的传统式讲解法
传统式讲解法是先给出定理内容,再进行定理条件分析,最后论证定理结论.
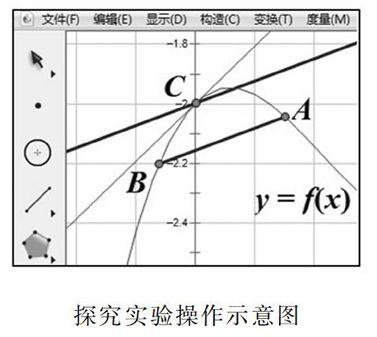
为了便于说明,我们先给出罗尔定理和拉格朗日定理.
罗尔定理 如果函数 f(x)满足:(1)在闭区间a,b上连续;(2)在开区间(a,b)内可导;(3)在区间端点处的函数值相等,即f(a)=f(b),那么在 (a,b) 内至少存在一点a<ξ 拉格朗日中值定理 如果函数f(x)满足:(1)在闭区间a,b上连续;(2)在开区间(a,b) 内可导,那么在(a,b)内至少存在一点a<ξ 许多高等数学教材都是在给出罗尔定理内容、几何含义及证明后,提出如果去掉罗尔定理中的第三个条件,即区间两端点函数值相等,会得到一个新的定理即拉格朗日中值定理,然后是拉格朗日定理的几何图形表示,证法讨论,构造辅助函数进行定理证明.这种先给出定理再根据定理条件画几何图形进行分析论证的过程,不符合从感性认识到理性认识的认知过程,学生只能是被动地接受,限制了学生的思考探究,也不利于学生学习积极性的调动,使学生很难参与到这样一堂纯数学理论的学习中来.直接给出结论是灌输式的教法,不利于学生学习能力的培养.下面介绍一种探究式的教学法,这种方法可以锻炼学生发现问题、解决问题的能力. 二、拉格朗日中值定理的探究式教学法 本文采用探究式教学法,其具体研究方法是先提出问题,再进行探究实验,接下来进行归纳总结,最后论证结论. 1.提出问题 首先让学生回忆罗尔定理的内容及几何含义.学生思考回答后,教师可以利用多媒体在屏幕上展示罗尔定理内容及几何含义的图形.由罗尔定理的学习学生已经知道,若定理的三个条件全部满足,则在函数曲线上至少存在一点C,过C点的切线与区间两端点A,B连成的割线平行.这时可引导学生观察罗尔定理的几何图像提出问题:如果去掉定理中的第三个条件,即区间两端点函数值相等,是否还有切线与曲线两端点连成的割线平行?这时学生很自然地会想到去掉两端点相等的条件限制,那么端点A和B可能等高,也可能不等高.等高时是罗尔定理,不等高时结论会有什么变化?这个问题的提出可以引发学生的探究兴趣,但准确得出结论还有很大的困难,让学生带着疑问去观察接下来的动态演示的数学实验可以给学生形象直观的认识,进而突破难点. 2.探究实验 具体做法是:利用绘图软件,任选一个满足罗尔定理条件(1)(2)的具体函数,绘制该函数图像,在这条连续光滑的曲线上任意截取两点A,B,取这两点的横坐标构造区间a,b,连接AB得到曲线的一条割线,在曲线弧AB上任取一点C,过C点作出曲线的切线和割线AB的平行线,如图所示.接下来只需将点C从一个端点沿曲线AB移到另一个端点,观察过C点的两条线能否重合;若重合,次数是不是唯一的.可以改变不同端点值,重复实验几次.这一过程可以先由教师示范,学生观察.然后邀请学生自己改变曲线端点值,亲自动手实验.有条件的话,最好将学生分成不同的组,每组取可以取不同的函数演示操作.这样既增加了学生参与的人数,调动了学习积极性,同时也可以在有限的时间里让学生看到更多的不同的实验结果,增加学生合作交流的机会,培养学生的团队意识. 探究实验操作示意图 3.归纳总结 通过实验的直观观察,学生不难总结得出这样的结论:对于自己所取的函数曲线AB,在开区间(a,b)内至少存在一点,过该点的切线与割线AB平行.这时教师可以进一步提出问题:实验不管取多少函数都是某个具体的函数,结论具有特殊性,但实验结论给我们很好的启示.能否将结论推广到满足条件的一般函数?引导学生深入思考.让学生由感性认识上升到理性认识,掌握由特殊到一般的研究方法.进一步启发学生论证所有得用数学的推理证明,可以先设一个命题:如果函数f(x)满足:(1)在闭区间a,b上连续;(2)在开区间(a,b) 内可导,那么在(a,b)内至少存在一点a<ξ 4.论证结论 下面对这一命题进行证法分析.对这一命题的证明过程,实际上就是拉格朗日中值定理的证明过程,主要把握利用罗尔定理,构造符合该定理的辅助函数.辅助函数的构造方法有很多,这里就不一一介绍了,在探究式的基础上,介绍给学生一种较易想到的辅助函数构造方法.由结论出发,要想f′ξ=f(b)-f(a)b-a→f′ξ-f(b)-f(a)b-a=0,令φ′(x)=f′ξ-f(b)-f(a)b-a,則需φ′(x)=0,这时可以提出问题:使φ′(x)=0得函数是常函数,即φ(x)=C,可取C=0,从而φ(x)=f(x)-f(b)-f(a)b-ax,不难验证φ(a)=bf(a)-af(b)b-a=φ(b)满足罗尔定理条件. 证:作辅助函数φ(x)=f(x)-f(b)-f(a)b-ax,由命题条件可推得φ(x)在闭区间a,b上连续,在开区间(a,b) 内可导,且φ(a)=bf(a)-af(b)b-a=φ(b),即φ(x)满足罗尔定理的三个条件,则在(a,b) 内至少存在一点a<ξ 这样学生经过探究实验,归纳推理,得出结论:该命题是真命题.教师这时可以告诉学生这个证明过的真命题就是拉格朗日中值定理. 利用探究式学习知识时,可以适当引入数学常识的一些相关知识,既丰富了学生的知识面,也培养了学生的数学情感.比如在讲解拉格朗日中值定理时,可以介绍数学家拉格朗日的生平贡献,还可以引入和实际相关的问题,插入一些视频文件,丰富课堂教学.笔者曾在课堂教学中给学生介绍卫星发射的最佳位置拉格朗日点,以及我国发射嫦娥系列卫星的新闻视频,效果很好. 三、结 语 授人以鱼不如授人以渔.探究式的研究方法与传统方法相比,能更好地引导学生思考,提高学生分析问题、解决问题的能力,是今后教学中更值得研究探讨提倡的方法,但是整个设计过程要适合学生的实际能力,对教师素质提出了更高的要求,要求教师要在教学过程中不断探索、反思,努力提升自己的专业技能. 【参考文献】 [1] 同济大学数学系.高等数学(上册).高等教育出版社,2007年4月第6版:129-131. [2] 四川大学数学系高等数学教研室.高等数学(第一册).高等教育出版社,1995年3月第3版:148-151. [3] 刘玉琏,傅沛仁.数学分析讲义(上册).高等教育出版社,1992年6月第3版:203-207.

