EMD-ARI模型在大坝渗流预报中的应用研究

刘彩花，景 浩，成一雄，牛 月

（太原理工大学水利科学与工程学院，山西 太原 030024）

国内外统计资料显示，地下渗漏引起大坝发生安全事故的概率为20%，失事原因为渗流量增大、渗透坡降加大等[1]。我国1981年的调查结果表明，31.7%的大坝安全事故是由渗漏管涌引起的[2]。因此，对大坝进行渗流监测，通过建立恰当模型来监控大坝运行状态、预测大坝未来运行性状意义重大。

由于渗流序列体现出复杂的非线性、非平稳特征，可能包含周期性、趋势性及随机波动等成分，因此联合运用多种理论分析方法建立耦合模型取代单一模型预测成为研究趋势。本文利用经验模态分解法 （Empirical Mode Decomposition，EMD） 具有秉留原数据属性的特点及时间序列ARI(Auto Regressive Integrated)模型具有预测精度较高与先进统计性的优势，提出了EMD-ARI渗流耦合模型，将此模型应用于汾河水库左坝岸渗流量的预报中，并将预报结果与ARI单一时序模型的预报结果进行比较和分析，以期为大坝安全运行状态监控及模型构建提供参考。

1 理论分析方法

1.1 EMD-经验模态分解法

EMD[3]可将原始序列分解为若干阶频率不同的固有模态函数 (Intrinsic Mode Function，IMF)和一阶趋势项，分解步骤为:

（1）找出原始序列x（t）全部极大值点，进行3次样条函数法插值，得各时刻上、下包络线值xmax（t）、xmin（t） 及包络线均值 m（t）

（2） 求类距平值函数 h（t）

判断h（t）是否为固有模态函数的依据为:①h（t）函数的极值点个数与跨零点个数相等或仅相差1；②m（t）恒等于零。满足则h（t）为固有模态函数，否则将 h（t）作为原始序列重复步骤 （1）、（2），直至同时满足①、②为止。得到的一阶固有模态函数I1（t）及剩余值序列为

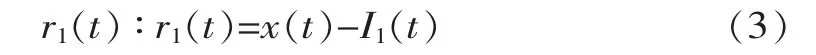
（3）以r1（t）为新序列，重复以上步骤，直至分解出所有阶IMF分量及一阶趋势项r（t）。

1.2 求和自回归模型ARI(p,d)

ARI[4,5]（p,d）模型是d次差分运算与AR（p）模型的组合，表达式为:

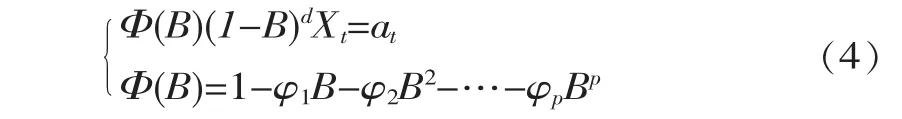
式中，Xt为原序列；φ1,φ2,…,φp为自回归系数；p 为自回归模型阶数；B为后移算子；B的次数表示后移期数；d为差分运算次数；Φ(B)为自回归系数多项式；at为零均值白噪声序列。

2 汾河水库E MD-ARI渗流模型开发

2.1 工程简介

汾河水库建于1958年，为大 (二)型水利枢纽，具有发电、防洪、灌溉等综合效益。水库于1990年建立了大坝渗流自动观测系统，监测内容包括左右坝基渗流、左坝岸渗流、古河床坝体绕渗、浸润线等，其中，左坝岸渗流采用三角堰观测，观测频率为每周一次，观测设备完好。本文采用2010年7月2日～2012年11月17日汾河水库左坝岸共125组渗流监测数据进行模型构建；采用2012年11月24日～2012年12月29日汾河水库左坝岸共6组渗流监测数据检验模型拟合结果与预报精度，部分渗流监测数据如表1所示。

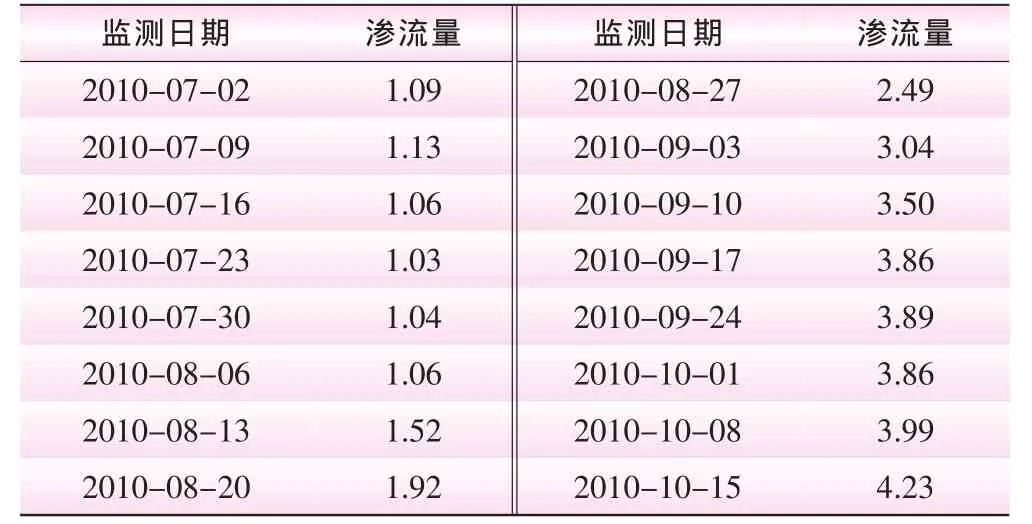
表1 汾河水库左坝岸部分渗流量监测数据L·s-1

2.2 EMD分解

基于MATLAB平台对汾河水库左坝岸渗流序列进行EMD分解，分解结果如图1所示。分解得4阶IMF分量与趋势项，经Hilbert变换及倒数运算后求得 4阶 IMF分量的平均周期分别为 23.8、43.6、148、222.7天，表明渗流序列可能存在23.8、43.6、148、222.7天这4个波动周期；1阶趋势项总体呈上升趋势，表明汾河水库左坝岸渗流量有随时间推移增加的趋势。

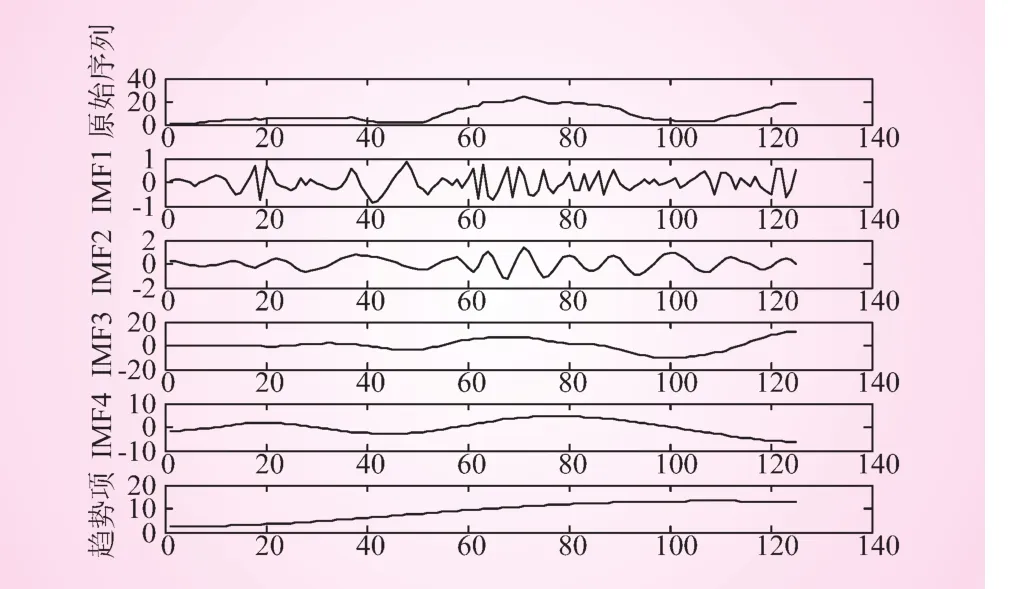
图1 汾河水库左坝岸渗流序列EMD分解结果

2.3 IMF分量及趋势项拟合

应用Fourier级数对4阶IMF分量进行周期拟合[6]，不考虑均值项的拟合结果为

应用线性方程对趋势项进行拟合，拟合结果为

式中，t为渗流量序列时间序号(1，2，…，125)。

2.4 剩余值序列ARI模型建立

水库渗流序列经提取可能周期与趋势项后得剩余值序列，对其进行时序分析建立ARI模型的步骤[7]为:

（1）剩余值序列平稳性检验。ADF单位根检验结果表明剩余值序列显著非平稳，一阶差分后平稳。

（2）差分序列的纯随机性检验。采用LB检验统计量对差分后的剩余值序列进行纯随机性检验,检验结果为LB统计量的P（Pr>ChiSq）值均小于0.05，说明该序列为非白噪声序列，满足时序建模条件。

（3）差分序列拟合AR模型。模型阶数由BIC准则确定，BIC值最小时相应模型阶数最优，其表达式如下

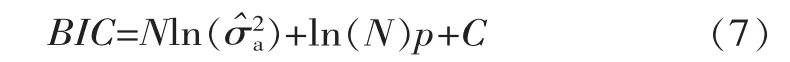
式中，BIC为信息准则函数；N为序列长度；p为模型阶数；C为常数；为模型残差方差的极大似然估计值。

根据BIC准则确定最优模型为AR（2），模型参数经检验极显著，还原差分后得ARI（2，1）模型表达式为

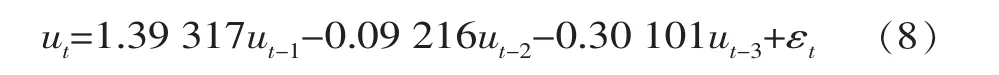
（2） 模型残差检验。 ARI（2，1）模型残差的检验结果为LB检验统计量的P（Pr>ChiSq）值均大于0.05，表明ARI(2，1)模型适合渗流序列。

2.5 汾河水库EMD-ARI模型建立

汾河水库EMD-ARI模型的结构为

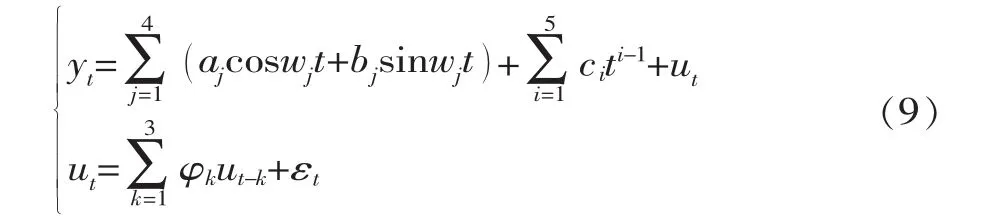
式中，yt为汾河水库左坝岸渗流量序列；aj、bj为相应各阶IMF分量的傅氏系数；ωj为相应各阶IMF分量的角频率；ci为趋势项各项系数；ut为汾河水库左坝岸渗流量剩余值序列；φk为时间序列ARI模型参数；ut-k为t-k时刻的剩余值序列；εt为模型残差项。

基于SAS软件平台运用Gauss-Newton[9]（高斯-牛顿）法对全部参数进行重构，所得EMD-ARI模型参数重构的最小二乘估计值如表2、3、4所示。

表2 IMF分量傅氏系数

表3 趋势项系数

表4 ARI模型参数

汾河水库EMD-ARI模型的回归方程为

3 汾河水库ARI渗流模型开发

水库左坝岸渗流序列只进行时序分析，经平稳性与随机性检验后确定最优模型为ARI(2,1)，对模型参数进行条件最小二乘检验，检验结果如表5所示。

表5 条件最小二乘结果

由表5可知，t检验统计量的P(Pr>|t|)值全部小于检验水平0.01，模型参数均极显著，将一阶差分还原后得ARI(2,1)模型的表达式为

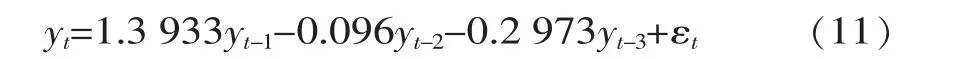
式中，yt为汾河水库左坝岸渗流量序列；yt－1为t-1时刻渗流量序列；yt－2为 t-2时刻渗流量序列；yt－3为t-3时刻渗流量序列；εt为模型残差项。

经参数检验后对ARI(2,1)模型进行残差检验，检验结果如表6所示。

从表6可以看出，ARI（2，1）模型残差的LB检验统计量的P（Pr>ChiSq）值均大于0.05，残差序列为白噪声，表明渗流序列可建立ARI（2,1)模型。

表6 ARI(2,1)模型残差自相关检验

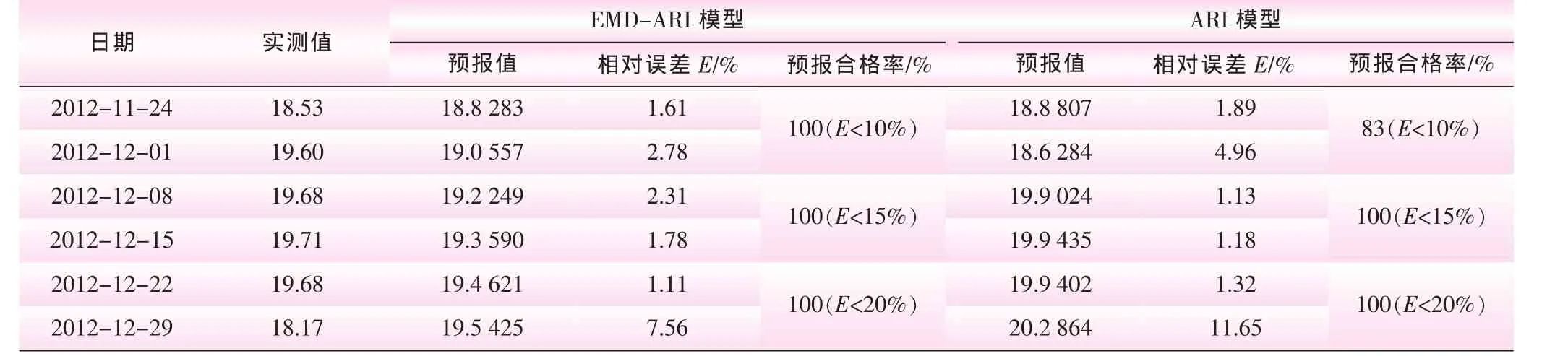
表7 渗流模型预报误差分析

图2 EMD-ARI渗流模型拟合

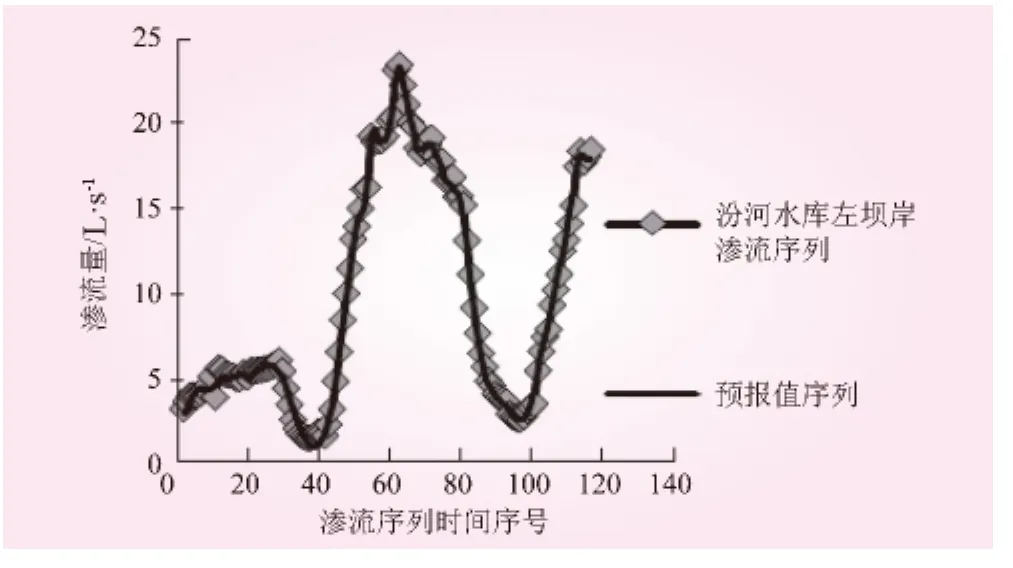
图3 ARI渗流模型拟合

4 汾河水库渗流模型预报结果的对比分析

（1）EMD-ARI模型与ARI模型的拟合结果分别如图2、3所示。从图2和图3可以看出，两个模型的预报值与实测值的吻合度均较高、拟合效果均较好。

（2）EMD-ARI模型与ARI模型的预报结果如表7所示。由表7可知，①EMD-ARI模型其预报值与实测值的相对误差E总体偏小；②EMD-ARI模型第6步预测的相对误差E为7.56%，小于ARI模型的11.65%；④E<10时EMD-ARI模型的预报合格率为100%，高于ARI模型的83%；④E<15，E<20时两模型的预报合格率均为100%，满足相对误差E小于20%的要求。

5 结 论

（1）汾河水库左坝岸渗流序列经EMD分解，得4阶IMF分量与1阶趋势分量，4阶IMF分量表征渗流序列可能具有的4个周期成分，1阶趋势分量表明渗流量随时间推移增加。

（2）EMD-ARI模型与ARI模型的相对误差呈先增后减再突变增趋势，即相对误差表现为跳跃特征，且第6步预测的相对误差的突变增表明随预测步长的增大模型预测精度降低。

（3）本文1步预测的时间间隔为7天，ARI模型第6步预测的相对误差为11.65%，误差较大，因此适用于进行5步预测，即预测汾河水库未来35天以内的左坝岸渗流量；EMD-ARI模型第6步预测的相对误差为7.56%，预测精度较高，可对汾河水库左坝岸渗流量进行6步预测。

（4）EMD-ARI渗流耦合模型的预报精度高于ARI渗流单一模型的预报精度，该法切实可行，可用于渗流预测。

［1］陈文燕,朱林,王文韬.大坝安全监测的现状与发展趋势［J］.电力环境保护,2009,25（6）:38-42.

［2］毛昶熙，段祥宝，李祖贻.渗流数值计算分析与程序应用［M］.南京:河海大学出版社，1999.

［3］赵雪花，安莉莉，袁旭琦.基于HHT和R/S分析的黄河上游年径流序列演变模式分析［J］.水电能源科学，2013，31（7）: 9-12.

［4］王燕.应用时间序列分析［M］.北京:中国人民大学出版社，2005.

［5］王振龙.应用时间序列分析（第二版）［M］.北京:中国统计出版社，2010.

［6］BOWERMAN B L,O’CONNELL R T.Forecasting and Time Seriers［M］.3rd ed.Brooks/Cole.Duxbury，United States America，1993.

［7］肖枝洪，郭明月.时间序列分析与SAS应用 ［M］.武汉:武汉大学出版社，2009.

［8］杨金芳，翟永杰，王东风，等.基于支持向量回归的时间序列预测[J].中国电机工程学报，2005，25（17）: 110-114.

［9］高惠璇，等.SAS系统 SAS/STAT软件使用手册 ［M］.北京:中国统计出版社，1997.