用数字化实验装置设计“闭合电路的功率问题”教学

张 宇

（北京市育英中学，北京 100036）

闭合电路的功率分配及相关概念是电路的一个重点内容，而输出功率随外电阻的变化规律是学生学习的难点.在教学中我运用电流和电压传感器来进行实验，成功地突破了重点和难点，取得了较好的教学效果.

1 出示问题，引发学生思考

问题1.在电动势与路端电压的关系式E＝U＋Ir两侧同乘电流I，得出EI＝UI＋I2r，等式中每1项各表示什么？

设计意图：通过学生思考和归纳，明确“电源总功率、输出功率、内阻消耗的功率”等概念.另外，通过引导学生分析能量的流向（能流图），理解闭合电路的能量转化是能量守恒定律的又一体现.

问题2.如图1，电源电动势E＝10V，内阻r＝2.0Ω，若滑动变阻器阻值分别为R＝0.5Ω、2.0Ω、3.0Ω，求：（1）电源的总功率P总.（2）输出功率P出.（3）电源的效率η.把结果填入表1中.

图1

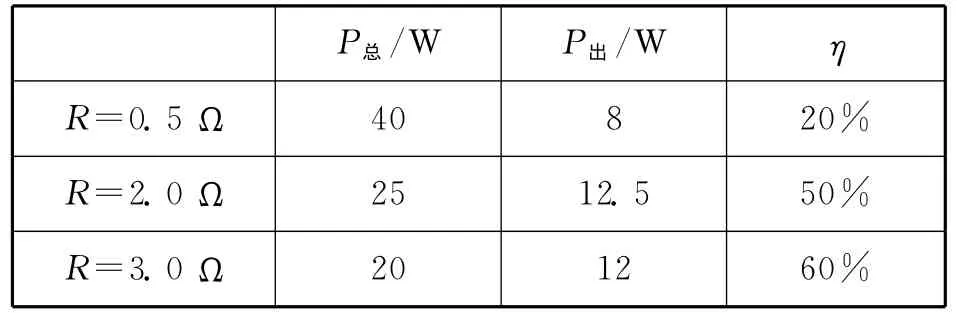
表1

问题3.观察数据变化规律，请回答：（1）电源总功率P总随外阻R如何变化？并分析原因.（2）电源的效率η随外阻R如何变化？并分析原因.

设计意图：学生通过数据分析，找到总功率和电源效率的变化规律，形成感性认识；再通过演绎推理，分析变化原因，培养学生的分析能力.

问题4.电源输出功率P出随外阻R如何变化？

设计意图：学生观察数据，发现电源输出功率P出随外阻R并不是单调变化的，很多学生认为P出随R先增大后减小.再进一步追问：仅看这3个数据，能确定2者的变化关系吗？显然不能.要明确2者的变化关系，应该怎么办？需要研究P出-R函数关系的增减性.这样可以培养学生“发现问题”的问题意识.

2 应用数学处理物理问题

首先明确问题：研究输出功率P随外电路电阻R如何变化.其中外阻R为自变量，输出功率P为因变量（函数），引导学生进行数学演绎，推导的思路是把自变量R集中在分母上，得

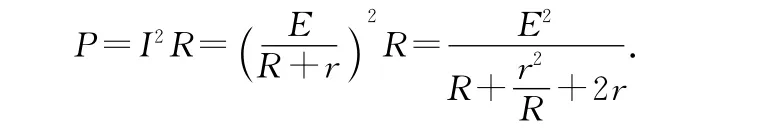
强调：电源参量电动势E、内阻r为定值，变量只有外阻R，我们只需要研究表达式学生在数学课学习过“均值不等式”：若ab＝定值，则当a＝b时，a＋b有最小值.学生很自然得出当R＝r时有最小值，此时输出功率P最大.

进一步设问：通过刚才分析，我们只得出输出功率P有最大值，而我们的问题“电源输出功率P出随外阻R如何变化？”并没有完全解决.要解决这个问题，我们需要知道数学函数y＝ax＋（a＞0，b＞0，x＞0）的增减性.数学学得好的学生马上反应过来：可以用“对勾函数”的性质来分析.为了让学生对这个函数理解得更深刻，笔者用Excel的数表功能作出函数y＝x＋的图像，如图2.

图2

设计意图：设计时充分考虑学生的数学基础，利用数学函数以及不等式知识，引导学生利用数学知识解决物理问题.这样的情景设置能有效地唤起学生的学习兴趣，使学生进入良好的学习状态.

3 实验检验

经过演绎推理得出的物理结论是否正确，必须通过实验验证.通常需要利用如图3所示的实验电路，改变滑动变阻器R的阻值，利用电流表和电压表测出几组U、I值，求得滑动变阻器的阻值R及其功率P，做出P-R图像.在教学中为节约教学时间，突出研究的核心问题，笔者利用了数字化实验装置，实现数据实时采集和实时处理.这里使用电流和电压传感器，采集的数据由电脑直接做出P-R图像.实验结果如图4.

图3

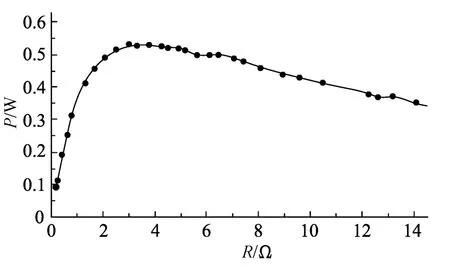
图4

由P-R图像可以看出，滑动变阻器的功率P随其阻值R先增大后减小；当外阻R接近4Ω时输出功率最大.

用同一组实验数据再做出电源路端电压U随电流I变化的U-I图像，如图5，由电脑直接拟合出来的表达式U1＝-3.6711I1＋5.3439，可知电源内阻r＝3.7Ω.这样我们就验证了“当R＝r时，输出功率最大.”

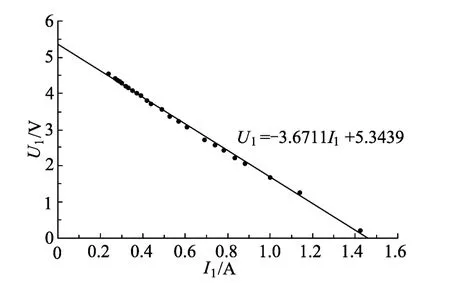
图5

设计意图：如果课堂上用电流表、电压表来进行实验，并做出P-R和U-I图像，几乎是一件不可能完成的任务.而本节课充分利用传感器的辅助教学功能，利用数字化实验装置P-R和U-I图像瞬间就得到了，节约出大量时间引导学生进行深度的思维训练，提高课堂的效率.电源输出功率P出随外阻R的变化规律不单单通过数学推理得出，而且还通过实验验证，使学生更信服，更愿意接受.本实验设计的巧妙之处在于：利用电脑作出U-I图像，求得电源内阻，从而验证了“当R＝r时，输出功率最大.”使实验结果和数学分析完全一致，让学生进行了一次完整的科学探究过程，在得出物理规律的同时，也培养学生的实验能力.

4 巩固提升

为了加深对规律的理解，提出以下问题：如图6，电源电动势E＝6V，内阻r＝1Ω，电阻R1＝9Ω，滑动变阻器R的最大阻值为20Ω，在其滑片由左端滑到右端的过程中，滑动变阻器R消耗的功率如何变化.

图6

设计意图：学生自然想到用刚刚得到的规律“当R＝r时，输出功率最大.”来分析，但题目中多了个定值电阻R1，引导学生用等效法，R1和电源可等效成一个电动势为E＝6V、内阻为r＋R1＝10Ω的电源.所以滑片由左端滑到右端，滑动变阻器R功率先增大后减小，当R＝10Ω时它的功率最大.等效法是常用的物理方法，通过在课堂上渗透学科思想，提高学生的知识迁移能力和分析解决问题的能力.

本节课通过“提出问题—学生猜想—数学推导—实验验证—规律应用”让学生体验完整的研究过程，学生经历了理论探究和实验探究，在知识的生成过程中发展思维能力和实验能力.