水泵水轮机特征参数的非线性统计分析
曾 威,杨建东,刘艳娜
水泵水轮机特征参数的非线性统计分析
曾 威1,2,杨建东1,2,刘艳娜1,2
(1. 武汉大学,武汉 430072;2. 水资源与水电工程科学国家重点实验室,武汉 430072)
本文收集了国内27套已投入运行的水泵水轮机全特性资料,根据收集资料计算出在水轮机工作区和水泵工作区高效点的比转速,通过高斯牛顿法求解比转速与工作水头和扬程的统计公式,并绘制了其置信区间。同时,研究了特征点单位参数与比转速的相关关系,并绘制了单位转速的预测区间,提炼了比较有规律的特征,对于水泵水轮机的设计和选型以及全特性曲线的构造具有一定参考价值。
水泵水轮机;抽水蓄能电站;比转速;非线性统计;回归分析;置信区间;预测区间
0 前言
抽水蓄能电站具有储能发电功能,解决了电能不易存储的矛盾,有效调节了电力系统发供用的动态平衡问题,目前得到了大力的发展[1]。水泵水轮机的选择对抽水蓄能电站的运行有很大的影响,故有必要从理论上分析各特征参数的相关性,对水泵水轮机比转速进行各参数匹配,使选择的水泵水轮机工作范围远离不稳定区。
文献[1]中介绍了国外对抽水蓄能电站水头、扬程与比转速的统计分析结果,但统计年代较为久远,绘制的7座国内抽水蓄能电站的数据与统计分析结果相差较大,有必要重新进行统计分析。且水头、扬程与比转速的相关性本身就不高,有必要绘制一个可靠的拟合区间以供参考。另外,由于缺乏全特性曲线数据,之前学者统计分析都是针对具体电站设计指标,如额定点数据,而对水泵水轮机高效点数据的统计分析会对设计和选择新机型有更大的参考价值[1]。水泵水轮机的特征点包括其高效点,克里夫琴科[2]对特征点进行了一定的经验性分析。黎中原[3]对常规水轮机水头与比转速进行包络分析,可供常规电站参考。赵林明[4]针对贯流式水轮机,综合考虑叶片数和工作水头得到比转速统计公式。刘建红[5]综合考虑生产年代、厂家和工作水头得到常规电站比转速统计公式。国内抽水蓄能电站发展迅速,对水泵水轮机也进行统计性分析十分必要。
本研究收集了27套不同比转速的水泵水轮机全特性曲线,涵盖了国内大部分已建成抽水蓄能电站的水泵水轮机。采用非线性回归模型以及置信区间和预测区间的统计学方法[6]研究了比转速与水头、扬程以及特征点单位参数的相关关系,对于水泵水轮机的设计和选型以及全特性曲线的构造具有一定参考价值。
1 全特性曲线特征点及比转速



定义水轮机比转速为:
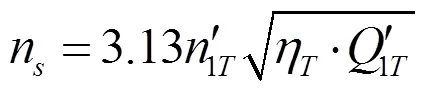
定义水泵比转速为:
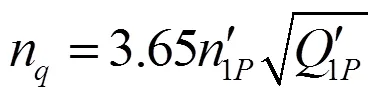
式中,下标、分别代表水轮机工作区和水泵工作区高效点的单位参数。比转速计算结果见表1。
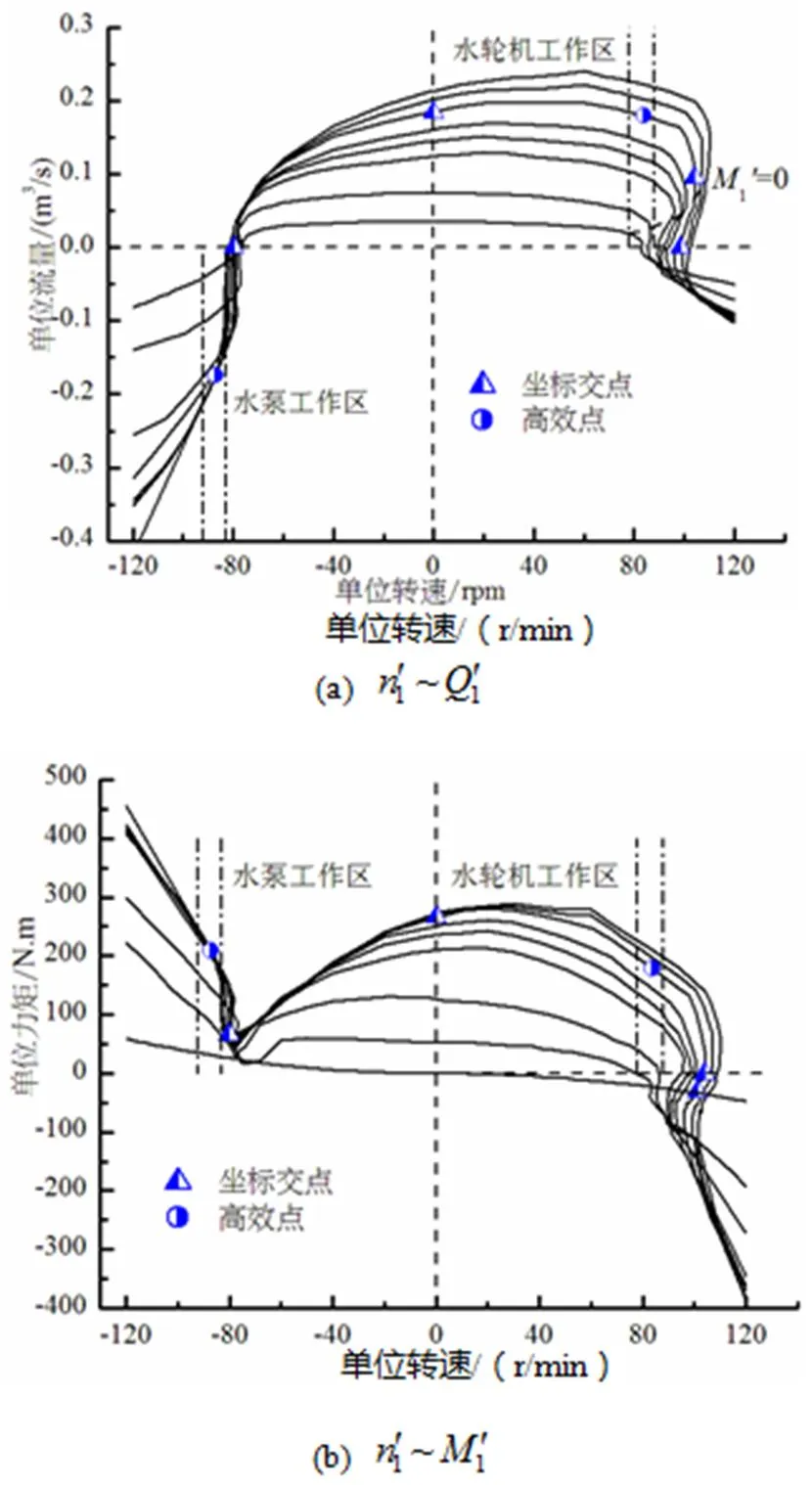
图1 水泵水轮机全特性曲线及特征点
表1 水泵水轮机比转速计算表

2 回归分析基本理论
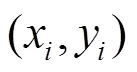
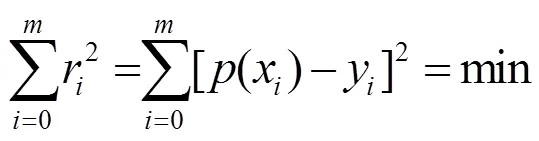
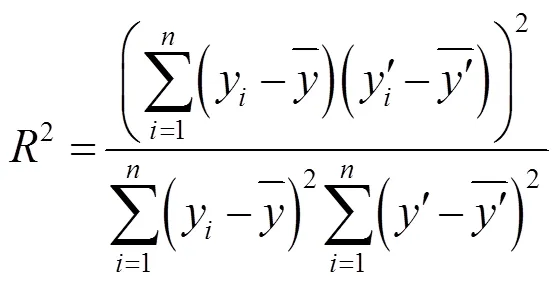
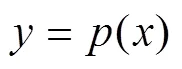
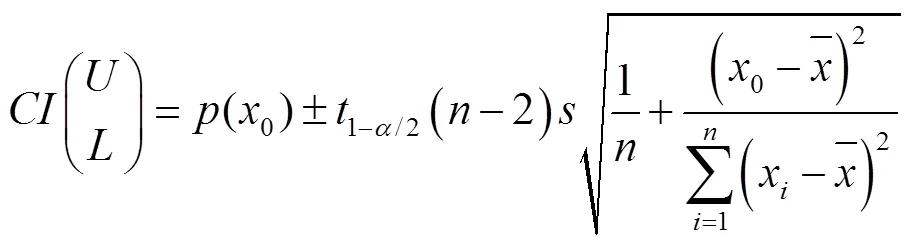

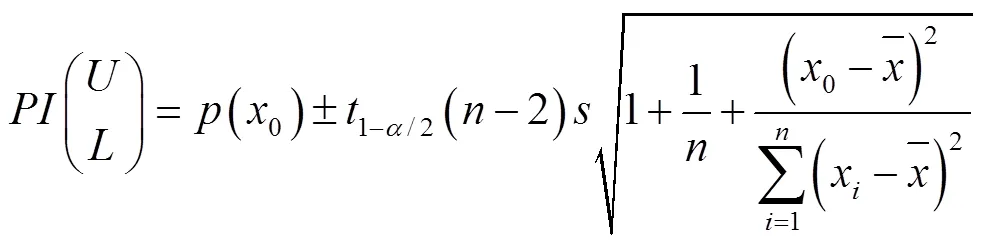
式中,代表预测区间。
3 水头及扬程与比转速的统计性分析

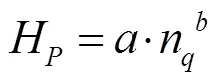
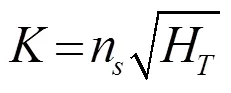

图2 水轮机比转速与额定水头统计分析

图3 水泵比转速与最大扬程统计分析
4 高效点单位参数与比转速的统计性分析
水泵水轮机的高效点是全特性曲线上重要的特征点,可以代表全特性曲线的变化规律,同时也是水泵水轮机设计和选型的参考依据。在水轮机工作区和水泵工作区分别存在一个高效点,其单位参数的统计数据如图4~6所示。
由统计资料可知,单位转速的变化范围很小,离散性较强,统计公式的意义并不大,故本文探讨了各高效点单位转速的预测区间。不同比转速水泵水轮机的高效点单位转速在拟合函数附近变化,且落在预测区间内部的概率为0.95。

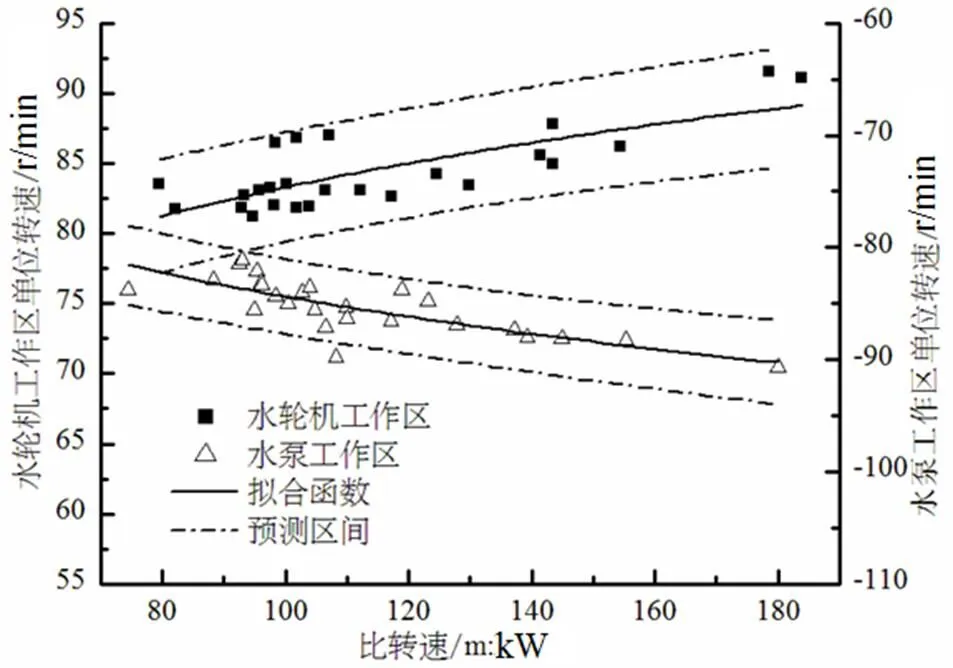
图4 高效点单位转速的统计性分析
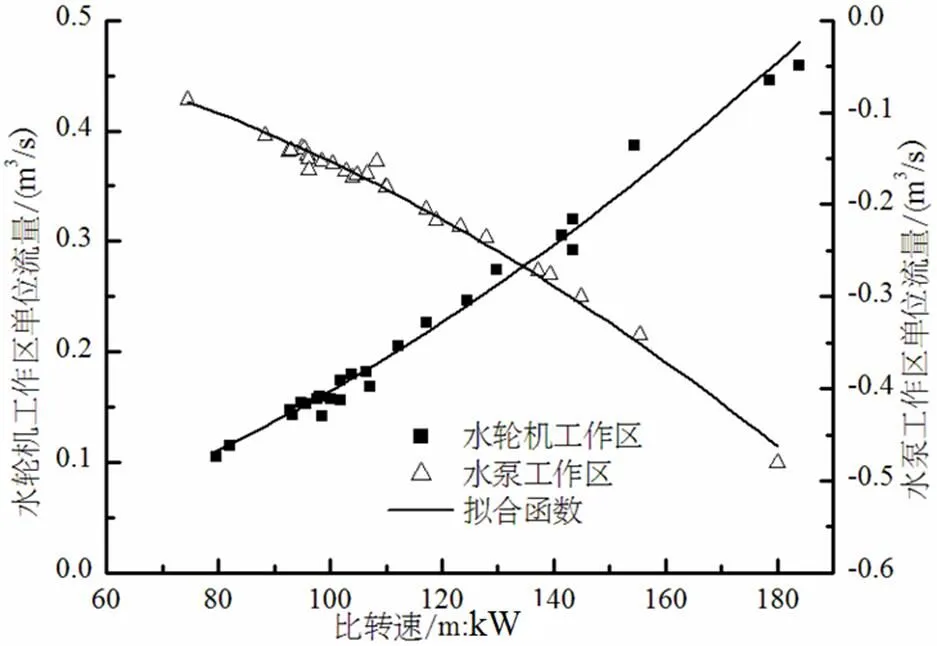
图5 高效点单位流量统计性分析
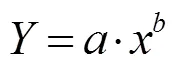
通过高效点单位参数的统计分析,可以提炼出如下结论:
两区域高效点单位转速的绝对值与比转速的相关关系很小,基本都在81~88之间变化,在预测区间内随比转速增加而增加,该区域的预测概率达0.95,具有很高可信度。单位流量和单位力矩与比转速是幂函数关系,指数均小于2,统计公式的复相关度达0.97,也具有很高的可信度。
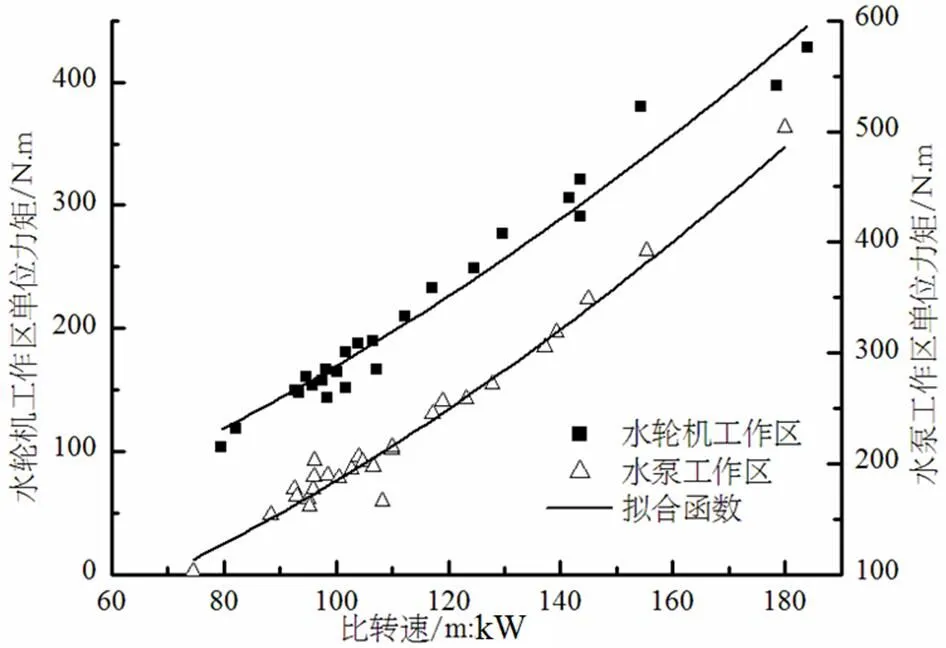
图6 高效点单位力矩统计性分析
5 坐标交点单位参数与比转速的统计性分析
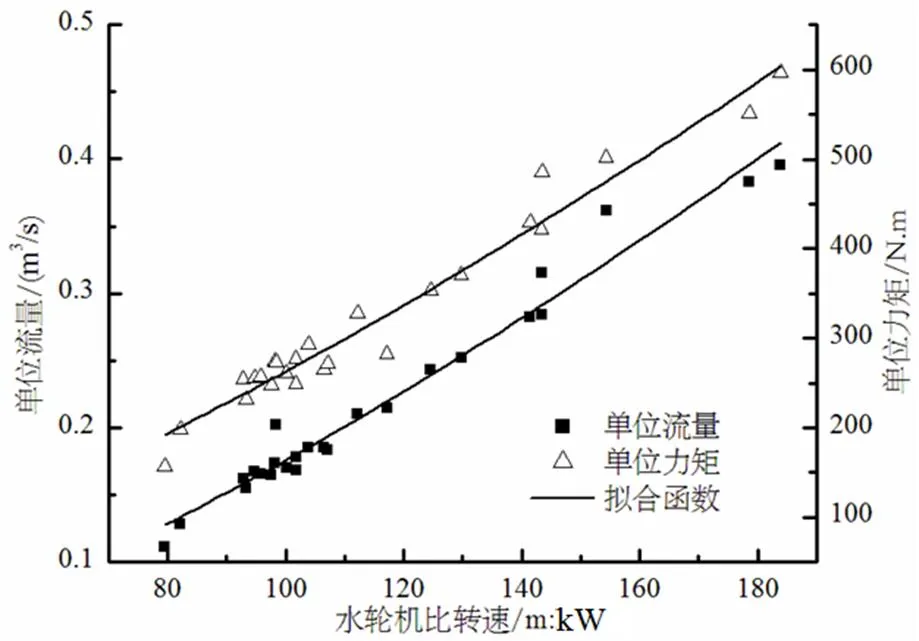
图7 轴交点单位参数统计性分析
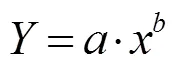
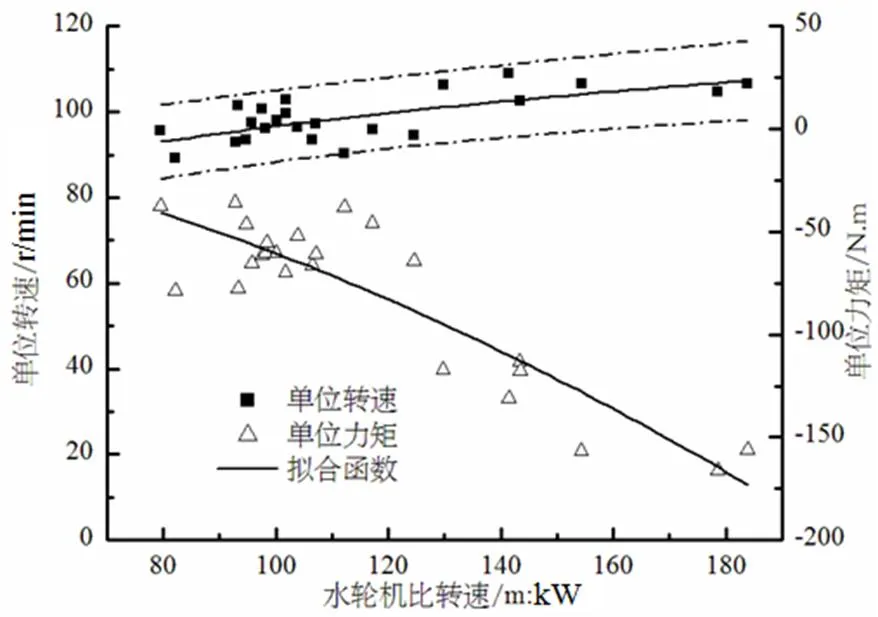
图8 轴交点单位参数统计性分析
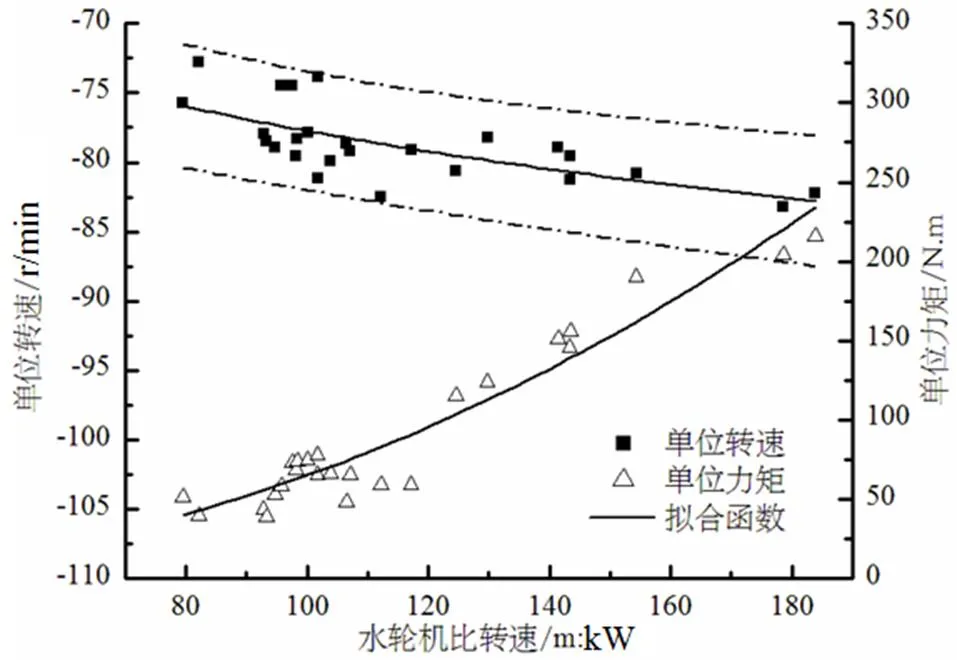
图9 轴交点单位参数统计性分析
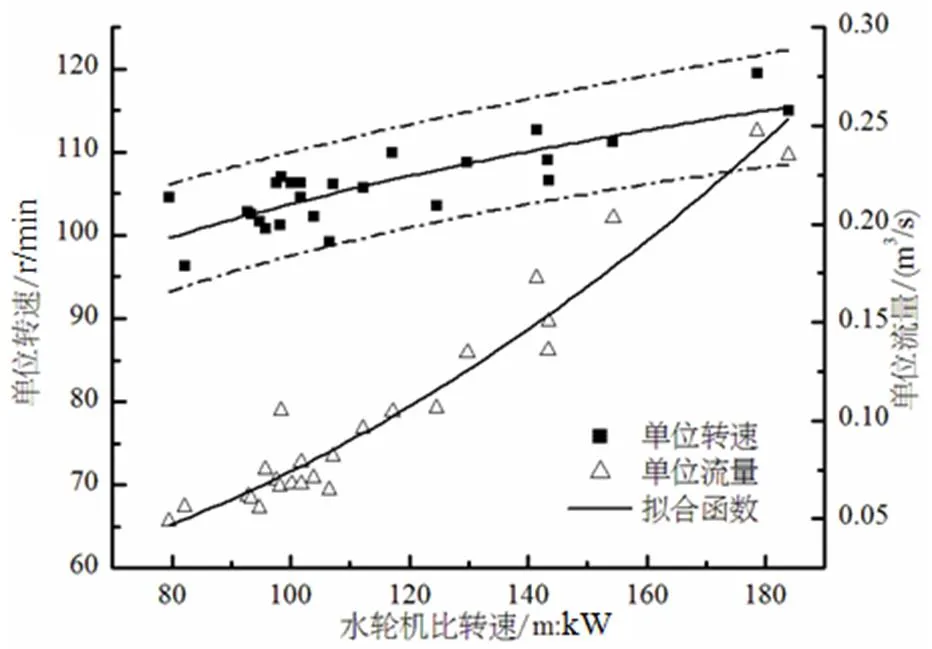
图10 轴交点单位参数统计性分析
通过对基准开度线坐标交点单位参数的统计分析,得出如下结论:
对于四个坐标交点,单位转速与比转速的相关性很低,单位流量和单位力矩与比转速的相关性较强。对于零转速特征点,单位参数与比转速的相关性最强。零流量点及零力矩点单位转速仅在小范围内变动,其绝对值在预测区间内随比转速增加而增加。零流量点单位力矩和零力矩点单位流量与比转速均为非线性递增关系。

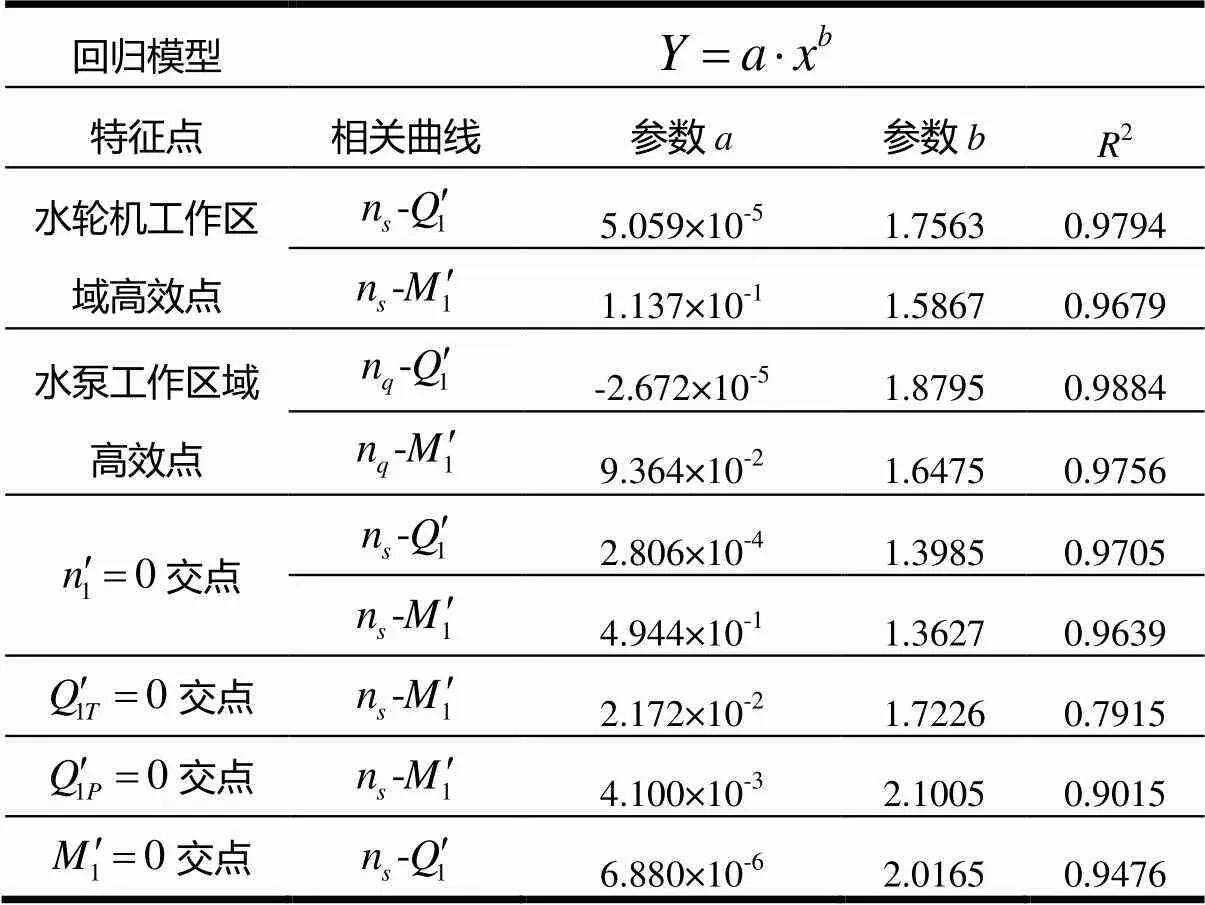
表2 特征点回归分析结果
6 结论
(1)通过非线性回归分析,得出了水头及扬程与对应比转速的统计公式,并绘制出了其置信区间,最佳拟合位于置信区间的概率为0.95,该结论可以作为水泵水轮机的设计和选型的参考依据。
(2)对水泵水轮机在水轮机工作区和水泵工作区最高效率点及基准开度线坐标交点的单位参数与比转速进行了相关性分析,得出了统计表达式,并绘制了单位转速随比转速变化的预测区间,同时提炼了这些特征点的变化规律。这些特征点统计公式和规律相比对电站具体设计指标的统计方法更能为水泵水轮机设计和选型提供帮助,同时该成果也可用于局部特性曲线向全特性曲线的扩展。
[1] 梅祖彦. 抽水蓄能发电技术[M].北京: 机械工业出版社, 2000.
[2] Г.И.克里夫琴科. 水电站动力装置中的过渡过程[M]. 北京: 水力出版社, 1981.
[3] 黎中原, 杨建东, 李进平. 水轮机比转速与额定水头的统计方法探讨[J]. 水电能源科学, 2008, 26(4):163-165.
[4] 赵林明, 张变梅. 贯流式水轮机比转速的统计分析[J]. 水力发电, 2012, 38(6): 60-61.
[5] 刘建红, 郑莉玲, 程乐安. 统计分析水轮机比转速ns的一种新方法[J].华北水利水电学院学报, 2000, 21(1): 64-65.
[6] 马逢时, 周暐, 刘传冰. 六西格玛管理统计指南-MINITAB使用指导[M]. 北京: 中国人民大学出版社, 2011.
Non-linear Statistical Analyses on Characteristic Parameters of Pump Turbines
ZENG Wei1,2, YANG Jiandong1,2, LIU Yanna1,2
(1. Wuhan University, Wuhan 430072, China; 2.State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan 430072, China)
27 groups datum of synthetic characteristic curves of pump turbines in China have been collected. Based on the datum, the specific speeds corresponding to the optimal operating points in the turbine working regions and pump working regions have been calculated. The statistical formulae of water heads and pumping heads to specific speeds have been worked out through Gauss-Newton method, and the confidence intervals have been figured out. On the other hand, the correlations between the unit parameters of the specific operating points and the specific speeds have been studied, and the prediction intervals have been applied to the unit rotational speeds. Through the correlations analyses, it is possible to exact the regular characteristics, which can be applied to design and select a pump turbine. Meanwhile, it offers valuable reference for generating the characteristic curves.
pump-turbines; pumped storage power station; nonlinear statistics; specific speed; correlation analysis; confidence interval; prediction interval
TV734.1;TV743;TK730
A
1000-3983(2014)02-0044-05
国家自然科学基金重点项目:基于空间曲面的水泵水轮机全特性及过渡过程的研究(51039005)
2013-08-15
曾威(1992-),男,湖北应城人,武汉大学水利水电学院,水资源与水电工程科学国家重点实验室,主要从事水泵水轮机特性和抽水蓄能电站过渡过程研究,硕士研究生。

审稿人:覃大清

