电磁弹射用永磁无刷直流直线电机非换相期间推力分析及补偿
姬新阳,汤子鑫,宫福红,黄旭东,谷 庆
电磁弹射用永磁无刷直流直线电机非换相期间推力分析及补偿
姬新阳1,汤子鑫2,宫福红1,黄旭东1,谷 庆1
(1. 中国洛阳电子装备试验中心,河南孟州454750;2. 总装备部南京军事代表局驻福州地区军事代表室,福建福州350003)
在电磁弹射中要求推力恒定,而速度的增大会引起推力下降,需要进行补偿。在非换相数学模型的基础上,求解得到电流及推力表达式,并分析了速度、电压、占空比对其影响。本文结合电磁弹射推力波形特点,定义、推导出推力波动,并分析各参数对推力波动的影响。对速度增大引起推力下降,提出通过调整电压和占空比的方法进行补偿。最后,通过计算得到不同速度对应的电压和占空比,给出推力曲线和推力波动,验证了算法的正确性和可行性。
永磁无刷直流直线电机;速度;非换相期间;电压;占空比
0 前言
永磁无刷直线直流电机具有推力大、可控性好、效率高、结构简单等特性,被应用到电磁弹射[1-3]中。在电磁弹射过程中,永磁无刷直线直流电机一般要求工作在恒推力条件下,其工作速度可达到几十甚至上百米每秒,并且工作电流大、电压高。因此,推力补偿时,需要对一些常用的方法和控制策略修正改进,以满足系统的要求。
对于常用电机,在速度恒定条件下保持推力恒定,工作在稳态条件下。电磁弹射的速度从零增大到最大值,并且要保持推力恒定,工作在瞬态。常用的控制策略要求工作在稳态条件下,如文献[4-6],对于电磁弹射,显然这些控制策略不能满足要求。闭环控制策略,输出量通过适当的测量装置将测量信号的全部或一部分返回输入端,使之与输入量进行比较,得到偏差信号,作为控制信号,作用于受控对象,使被控量趋于输入量。但电磁弹射工作速度高、电流大、电压高,对于电流等参数测量难度大、精度低,并且要求系统响应时间短。为了解决这一稳态,文中提出采用离线控制策略,在进行电机工作之前,通过理论分析计算出不同速度对应的电压和占空比。文献[7-8]对推力波动的分析考虑了低速、中速、高速三种情况,并没有进行全速度下的推力波动分析。文献[9]对推力波动进行分析是在速度不变的情况下提出的,没有考虑速度对推力的影响。文献[10-11]研究了不同PWM调制在无刷直流电机中的应用,通过改变占空比,调整电流,抑制推力波动。
在对推力和推力波动分析的基础上,提出了补偿速度引起的推力下降,同时推力波动满足系统要求的方法,并给出了计算电压和占空比的方法。
1 非换相期间数学模型及推力分析
动磁式双边定子永磁无刷直流直线电机二维XY平面模型见图1。动子铁心及永磁体构成了运动组件。三相定子绕组分别嵌入到动子两侧的定子槽中,弹射器的动子沿X轴方向运动。图1动子所处的位置即为初始位置。

图1 弹射器2维XY平面仿真
为了使弹射器工作时,动子组件受到的电磁力始终沿X轴方向,必须合理设置定子绕组中电流的方向与动子上永磁体的充磁方向。电磁弹射器工作在三相六状态模型下,驱动电路如图2所示。

图2 相绕组星形连接全桥式电路
永磁无刷直流直线电机采用三相星型六状态工作方式。供电方式采用PWM调制,如图3所示,横坐标为时间,纵坐标为电压。永磁无刷直线直流电机工作时,绕组按一定顺序换相,如对于任意一相绕组,在一个电周期内,先120o正向导通,然后60o不导通,再有120o反向导通,最后60o是不导通的。
在非换相期间只有两相导通,对于非换相期间的推力分析,以A、B两相为例。为方便非换相期间推力的分析,做如下假设:
(1)三相对称,反电动势为梯形波,平顶部分等于120o电角度;
(2)忽略电枢反应、齿槽效应、端部效应和磁路饱和的影响;
(3)相绕组的等效电感和等效电阻为常数;
(4)无论PWM信号为ON或OFF均不考虑续流的影响。

图3 PWM调制下电压波形
在A、B两相导通时,永磁无刷直流直线电机的等效电路为

图4 简化的等效电路
相应的数学模型为

解微分方程得

解得电流为

由式(2) (3)可得到在非换相期间A相电流为
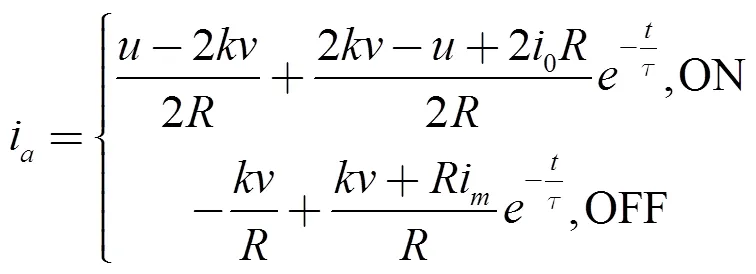

从推力公式中可以看出,电压增大,推力增大。占空比增大,PWM信号为OFF的时间减少,推力下降减少,因此推力随着占空比增大而增大。
推力大小与速度关系以速度为自变量,对推力求一阶导得
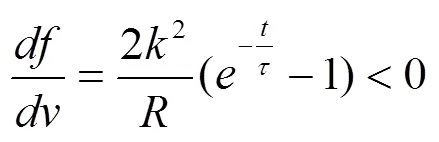
由于一阶导小于零,因此推力随着速度的增大而减小。
2 推力波动分析
合适地定义推力波动,对衡量推力波动的大小,及提出抑制推力波动策略具有很重要的意义。
在一个周期下的推力曲线,推力从最大值下降到最小值再增大到最大值,其中下降部分相对时间较短,相当于一个尖脉冲。因此推力波动要反映出脉冲对系统的影响,结合推力波形,在此定义推力波动如下
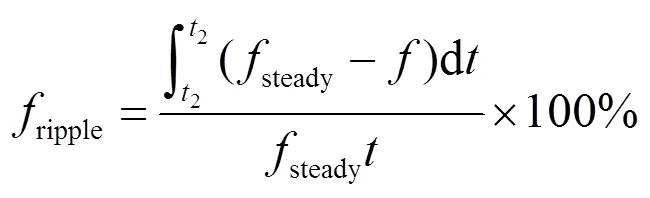


将公式(4)(8)(9)(10)代入推力波动公式(7)得推力波动公式为

从公式(11)分析得出,电压、占空比增大,推力增大,推力波动减小;速度增大,推力下降,推力波动增大。因此采用调整电压和占空比补偿速度引起的推力下降,同时满足系统对推力波动的要求是可行的。
3 推力的补偿
在电磁弹射过程中,要保持推力恒定,调整电压和占空比。直接采用解析方法计算量大,并且很难得到解析解。由于电压和占空比组成的解空间小,并且与推力的关系是单调递增,因此采用直接搜索算法,直接搜索算法是一种不需要任何关于目标函数梯度信息的最优化方法。与传统的最优化方法相比,传统的最优化方法需要目标函数的梯度或者高阶导数的信息来搜索一个最优点。直接搜索算法搜索当前点周围的一系列的点,然后找到一个目标函数的值低于当前点函数值的点。
以下为算法求解步骤:

(5)终止条件,速度达到设定值。
参数的选择很重要,合理的参数选择可以降低计算量,同时得到满意的解。
在进行电压、占空比初始值的选择时,通过公式(5)估算出所需的电压,然后设置电压略小于该值。电压步长太小,占空比的调节范围就减小;若太大,占空比调节不能满足要求,因为占空比的调节范围是有限的。所以电压步长的选择可以通过多次仿真,选择合适的步长。
占空比的选择需要在保证推力波动满足系统要求的条件下,计算不同速度下对应的占空比最小值,这样就得到了占空比最小取值。在仿真过程中调节步长大小,选择合适的步长。
4 仿真分析

图5给出了不同速度下满足系统要求的电压和占空比,其中占空比的取值很大,验证了之前的理论分析。图6给出了随着时间的变化,速度增大,经过补偿的推力曲线,横坐标为时间,纵坐标为推力。

图5 不同速度下的电压和占空比

图6 推力曲线图
图7给出了补偿后的推力波动曲线,满足推力波动最大为8%的情况下,满足系统的要求。

图7 不同速度下的推力波动
5 总结
在非换相数学模型的基础上,求解得到电流及推力,并定义推导出推力波动公式。通过对推力和推力波动的分析,得出通过调整电压和占空比补偿速度引起的推力下降,同时推力波动满足系统的要求是可行的。采用直接搜索算法,计算不同速度下所需的电压和占空比,仿真结果表明方法的可行性。
[1] Patterson D, Monti A, Brice C W. Design and simulation of a permanent-electromagnetic aircraft launcher[J]. IEEE Trans on industry applications, 2005, 18(18): 566-575.
[2] Michael R Doyle, Thomas Conway, Douglas J Samuel. Electromagnetic aircraft launch system EMALS[J]. IEEE Transactions on Magnetic, 1995, 31(1): 528-533.
[3] Doyle M, Sulish G, Lebron L. The benefits of electromagnetically launching aircraft[J]. Naval Engineering Journal, 2000, 112(3): 77-82.
[4] Xia C L, Guo P J, Shi T N. Speed control of brushless DC motor using genetic algorithm based on fuzzy controller[C]. IEEE international conference on intelligent mechanics and Automation Japan, 2004: 460-464.
[5] Yong Liu, Z.Q. Zhu and David Howe, Direct torque control of brushless DC drives with reduced torque ripple, IEEE transaction on industry applications, vol.41, no.2, 2005.
[6] Xia Changliang, Li Zhengjun,Yang Rong. Control system of brushless DC motor based on active-disturbance rejection controller [J]. Proceedings of the CSEE, 2005, 25(2): 82-86.
[7] 林平, 韦鲲, 张仲超. 新型无刷直流电机换相转矩波动的抑制控制方法[J]. 中国电机工程学报, 2005, 26(3): 153-157.
[8] Yong Liu, Z Q. Zhu, David Howe. Direct Torque Control of Brushless DC Drives With Reduced Torque Ripple[J]. IEEE Transaction Ind.Applicat, 2005, 41(2): 599-608.
[9] Dae-Kyong, Kwang-Woon Lee. Commutation torque ripple reduction in a position senseless Brushless DC motor drive, IEEE transactions on power elctronics, 21(6), 2006.
[10] 包向华, 章跃进. 5种PWM方式对无刷电动机换相转矩脉动的分析及比较[J]. 中小型电机, 2005, 32(6).
[11] 袁雄飞, 黄声华, 李朗如. 永磁无刷直流电机PWM调制方式研究[J]. 微电机, 2004, 37(5).
Analysis and Compensation of the Force During the Non-commutation in PMBLDCLM Used for EMLs
JI Xinyang1, TANG Zixin2, GONG Fuhong1, HUANG Xudong1, GU Qing1
(1. Luoyang Electronic Equipment Test center of China, Mengzhou 454750, China;2.General Equipment Department's military Representative at Fuzhou, Fuzhou 350003, China)
During the electromagnetic launchers (EMLs), the force should be constant, but increment of velocity will bring about the decrease of force, and it is expected to compensate force decline. The formula of current and force are deluded on the basis of mathematical model of non-commutation, and influence of velocity, voltage and duty cycle on the force are analyzed. The force ripple is defined and deluded combined with the work characteristic of EMLs, the influence on the force ripple is analyzed. It is feasible to compensate the force decline by adjusting the voltage and duty cycle, the force ripple is satisfied to the system at the same time. At last, the data of voltage and duty cycle corresponding to velocity is calculated, the simulation results verify the correctness and feasibility of theory and method.
PMBLDCLM; velocity; non-commutation; voltage; duty cycle
TM33
A
1000-3983(2014)02-0006-04
2013-08-17
姬新阳(1989-),2010年6月毕业于军械工程学院光学与电子工程系雷达工程专业,现从事雷达总体技术研究,助理工程师。

审稿人:宫海龙

