浅谈初中数学概念教学的现状及策略

闫芳

数学概念反映数学知识的本质属性，是学习数学知识的基础。通过对数学概念的认识与理解，能够帮助学生研究基本数学问题，形成一定的数学基本技能。从这点说，数学概念教学尤为重要，这要求教师不仅要重视数学概念教学，同时要启发学生在对所研究的对象进行分析、综合、抽象的基础上讲清概念的形成过程，理解概念的根本内涵，帮助学生运用概念分析、解决问题，以此为基础，逐步提高学生个体的数学素养。

一、初中数学概念教学的现状

初中数学概念教学的现状：很多教师不重视概念教学；部分教师重视但却不会教；有些教师分不清概念教学的主次关系；更有甚者，他们有对概念教学要求不当等不良倾向。

概念是数学知识的基础，是数学思想与方法的载体。但有的教师不重视概念教学，错误认为概念教学浪费时间，不如做几道题目实在。他们对概念的教学往往是蜻蜓点水，一带而过，而将课堂大部分时间花在定理、法则的推导与应用上，不知道这完全是本末倒置、事倍功半的做法。

有的教师对概念教学只着重于揭示概念的描述（定义），没有揭示概念的内涵与外延，不交代“三位一体”，这种不会教，既缺乏对数学概念知识本身的科学了解，又缺乏对概念教学应有的技能；部分教师对概念教学分不清主次，没有抓住概念中的核心关键词；更有教师错误认为概念教学就是让学生多读、多写，这样记住概念即可。

二、初中数学概念教学的一般策略

1.重视数学概念的认识过程

数学教学过程中如果只注重概念的呈现过程，直接将概念传授给学生，让他们在似懂非懂的基础上死记硬背，机械记忆，这样他们不会对数学知识有根本的认识，数学综合能力的发展也会受限。因此，教师要注重概念形成过程的教学，让学生充分体验概念是如何建立的，这样能有效帮助学生理解概念。

例如，对于代数式的概念教学具有一定的抽象性，学生不易理解，如果仅让学生记住代数式的形式特征，这样就不利于学习以下的“用字母表示数的意义”。所以，我们需要通过下面的操作活动，理解具体的代数式。

问题一：让学生用火柴棒按下面的方式搭正方形，并请填写好下表。

正方形个数123……100……n

火柴棒根数

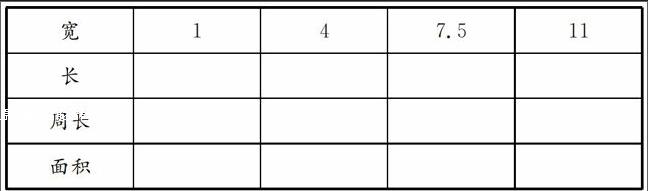
问题二：有一些矩形，长是宽的3倍，请填写下表。

宽147.511

长

周长

面积

通过以上具体的两个实际问题，让学生体会“代数式”的形成过程，从特殊到一般的过程中逐步过渡到建立“代数式”。最后教师给出“代数式”的准确定义，符合学生的认知规律。

2.在对概念理解的基础上，帮助学生建立理性认识

对重要的概念进行必要的识记是学习概念的基础，同时需要在识记基础上准确理解，逐步建立对概念的理性认识。在教学过程中，对一些概念容易混淆不清，产生错误，教师应有意识地把容易混淆的概念放在一起，通过分析比较，找出它们的联系与区别。如在学习线段、直线、射线的概念时，教师可以将之放在一起进行比较，分别从端点的个数和长度两个方面来区分。再如，学习中心对称与轴对称时，可以引导学生在操作活动中，感受到轴对称是在空间中折叠的过程，中心对称是在平面中旋转的过程，教学时应让学生比较区别，加深对不同概念的理解。

3.重视对概念的巩固，培养学生应用概念解决问题的能力

（1）通过已学概念来学习新的概念

数学概念的学习有时候不是独立的，而是彼此之间相互联系的，教师可以根据教学实际，将概念教学串联起来，不仅巩固已学概念，对新概念的学习也可奠定基础。例如，学习关于对一次函数的定义时，可以首先让学生复习已经学习过的函数的定义，弄懂函数概念中的变量之间的关系，理解“变化而变化，确定而确定”的含义，以此为基础学习一次函数就水到渠成了。

（2）利用课堂小结及时加深学生对概念的巩固

课堂小结引导学生善于总结，以概念为线索，把关联概念、派生概念串连成线，将课堂的数学知识复习寓于概念复习过程中。这样既帮助学生加深对概念的理解，又有利于发展学生的创造性思维。

（3）重视对概念的应用训练

以数学概念为基础，可以通过合情推理与演绎推理得到很多定理、法则等，这些都是学习数学的基础。所

以对概念的应用能力训练应该是课堂训练的重点，更应是多方面的、全方位的。它包括形象应用、抽象应用和综合应用，其中概念的形象应用包括“正、逆”两个方面。

例如，学习合并同类项的概念时，可以配备如下一组练习，加强对合并同类项概念的理解。

①已知xmy2与-3x3yn是同类项，则m=，n=

②下列合并同类项结果是否正确？并指出错误的地方。

15y2-5y2=10（）8x-3x=5x2（）

2x+3y=5xy（）16a2b-8b2a=8（）

③合并同类项。

2a+2b-7a-b；

2a2b+5ab2-4ab2-7a2b；

6-4ab-b2+7；

6b-3a3+1+a3-2b；

2y+6y+2xy-5

④思考：有这样一道题：“当a=13.58，b=9.07时，求多项式7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3的值。”有同学指出：题目中a=13.58，b=9.07是多余的。你认为这种说法有道理吗？

这样从基本题到能力题的设计，逐步提升学生对合并同类项概念的理解，从直观形象到抽象理性的认识，充分反映了同类项的本质属性。当然概念教学中，针对不同的概念，对学生的要求也应有所不同，对于一些次要不影响学生学习和学生一时难以深刻理解但又必须引入的概念，在教学中应对其定义作淡化（或者说浅化）的处理。

总之，数学概念是数学教学的重点内容，也是学生必须掌握的重要基础知识之一，对于数学基本技能的形成与提高有着重要的作用。在概念教学中，教师不仅要重视而且要讲究教学方法，注重概念的形成过程，在对概念的理解基础上，帮助学生建立理性认识；同时对于基本概念的理解要搞清内涵与外延，弄清概念之间的区别与联系，记忆概念注意关键词语和分析概念。

参考文献

[1]梁惠标.新教材数学概念教学的几种做法[J].广东教育，2004（5）.

[2]徐斌艳.数学教育展望[M].上海：华东师范大学出版社，2001.

[3]濮安山.中学数学教学论[M].哈尔滨：哈尔滨工业大学出版社，2004.

[4]教育部.数学课程标准[M].北京：北京师范大学出版社，2001.

（责任编辑黄晓）endprint