MURA编码辐射成像系统的解码方法

赵翠兰 陈立宏 李勇平

1（中国科学院上海应用物理研究所 嘉定园区 上海 201800）

2（中国科学院大学 北京 100049）

3（中国科学院核辐射与核能技术重点实验室 上海 201800）

4（宁德新能源科技有限公司 福建 352100）

传统的核辐射成像系统采用针孔式的准直器虽然能实现较高的空间分辨率，但探测效率非常低，因此其应用受到限制。1961年Mertz等[1]提出的编码孔成像技术为新型核辐射成像设备的研制提供了理论依据。他们采用的编码孔径为菲涅尔波带板(Finel Zone Plate, FZP)，它采集光子的效率要比传统的单针孔高得多，但是FZP只有在直径无穷大时才会有较好的相关特性。随着编码孔成像技术的发展，相继出现了随机阵列(Random arrays, NA)编码板、非冗余阵列(Non Redundant Arrays, NRA)编码板、均匀冗余阵列(Uniformly Redundant Arrays, URA)编码板，其相关特性有了很大的改善。URA阵列是1978年Fenimore等[2]提出的，很快在X射线、g射线星体成像以及g相机等远场成像领域得到广泛应用，其优点在于在有限大小内具有理想的相关特性，开孔率高因而能显著提高探测器对射线的收集率，在保持针孔成像较高分辨率的基础上，提高了信噪比(Signal to Noise Ratio, SNR)和系统的灵敏度[3]。1989年Gottesmen[4]在URA的基础上提出了修正均匀冗余阵列(Modified Uniformly Redundant Arrays,MURA)。它兼顾URA阵列的所有优点，而且可以排列成方形使得加工与使用都更为方便。

编码孔成像技术常用的解码算法有最大似然-期望最大化(Maximum Likelihood-Expectation Maximization, MLEM)迭代算法、δ 解码(δ decoding)算法和精细采样平衡解码(Finely sampling balanced decoding, FSBD)算法，MLEM迭代算法虽然在效果上可以达到最优，但是算法本身比较复杂，迭代计算需要很长时间才能获得到较好的收敛性；相比较而言，后两种算法更简单，收敛速度快，在模拟仿真试验时图像重建的速度更快，因此仅采用δ解码算法和FSBD算法为后续的实验做理论指导。硬件平台方面我们已研发出较高分辨率的探测器模块[5]，并设计了4个MURA 19×19循环周期排列的钨铅合金编码板[6]。在MATLAB环境下对解码算法进行编程实现，对它们的成像质量进行了对比研究，并且对单点源和多点源的图像重建进行了仿真实验和实际验证。

1 解码矩阵算法

对探测器上得到的编码板投影数据进行处理，从而恢复出放射源分布图的过程称为解码，也叫做图像重建。衡量编码准直器性能的一个主要指标就是它的自相关特性（AGÄ是否趋近于δ函数，A为准直器阵列，G为解码矩阵），利用自相关特性进行图像解码，从而可以重建出放射源的分布图。A经过放射源投影后在探测器上得到的是A¢，对G进行相应的处理得到G¢，然后利用就可以恢复出放射源的分布图。

将探测器投影图像进行数字化处理，即将每个准直器小孔的投影离散化成为一个a×a的矩阵，a称为成像系统的采样数，且满足：

式中，pd是探测器上一个像素的大小；m是成像系统放大倍数；pn准直器小孔单元大小。如图1所示，图中a=4，准直器小孔的投影被离散化为一个 4×4的矩阵形式。

图1 准直器小孔采样示意图Fig.1 Schematic diagram of sampling hole collimator.

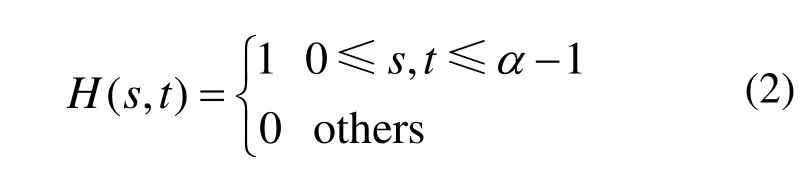
可以将A¢表示为：

式中，Ad是多个ra×ra的矩阵，它是由编码函数A扩展而来，将A中的每一个元素都扩展成a×a矩阵，并且矩阵中第一个元素与编码函数A中对应元素相同，其余元素都为0。为了方便A¢与解码矩阵G进行周期相关运算，必须将解码矩阵的每个元素同样扩展成为a×a矩阵，矩阵元素的选取直接影响到解码图像的质量[7]。根据a×a矩阵元素分布不同，解码矩阵算法分两类：δ解码与精细采样平衡解码。

1.1 δ解码

将G的每个元素扩展成a×a的解码函数采样矩阵时，a×a矩阵的第一个元素为1或−1，其余元素的值为0，G¢的1和−1的选取根据a=1时的解码矩阵而定。这种算法称为δ解码算法。

表5和表6采用相同的统计手段，表7描述了进口企业和非进口企业的New同Pnew均值，基于进口多样性指标排列结果得出进口企业的New以及Pnew值。对表7结果进行分析，New和Pnew的均值与进口多样性间呈现正相关性，两种企业的创新能力指标呈现显著差异性。非进口企业的产品创新能力比进口企业平均水平低，对两种企业的首组数据实施分析得到，两种企业的产品创新能力差异的取值条件是［62%,98%］；同第三组数据进行对比，差异高达85%～152%。在进口企业中，即使各组间差异幅度不明显，New与Pnew的均值也随着进口多样性指标增多而提高。

以 MURA 3×3编码板、采样数a=4为例，图2(a)、(b)分别为MURA编码板函数和a=1的解码函数，图2 (c)为δ解码函数。

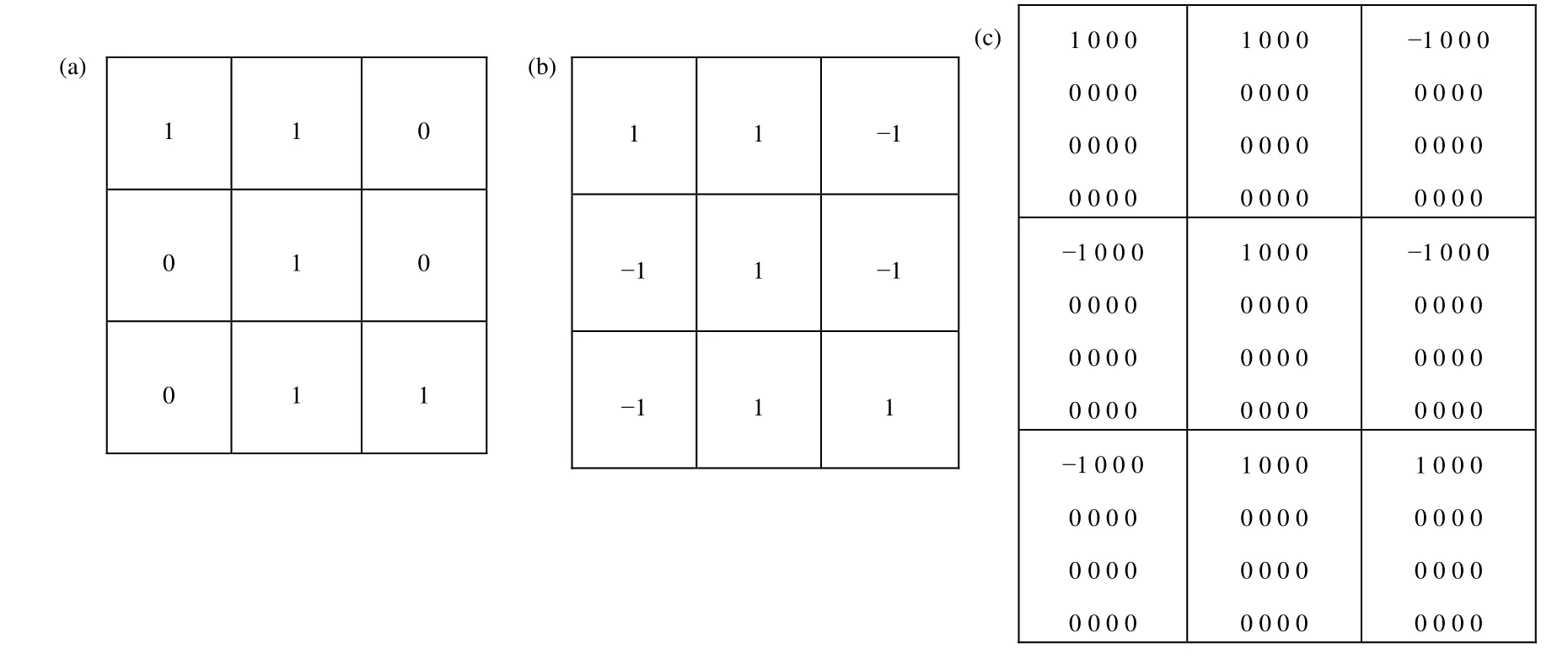
图2 MURA 3×3编码(a、b)及δ解码(c)Fig.2 MURA 3×3 coding (a, b) and δ decoding (c).

δ解码函数的点扩散函数(Point Spread Function,PSF)可以写为[6]：

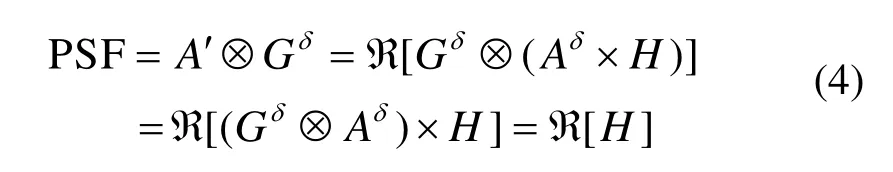
式中，Â为反演操作。

1.2 精细采样平衡解码

将G的每个元素扩展成a×a的解码函数采样矩阵时，a×a矩阵的每一个元素为1或−1，G¢的1和−1的选取根据a=1时的解码矩阵而定。这种算法称为精细采样平衡解码算法。图3为精细采样平衡码函数。

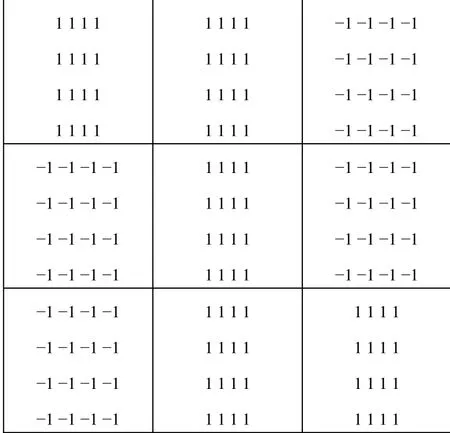
图3 精细采样平衡解码Fig.3 Finely sampling balanced decoding functions.

由以上发现G¢可以表示成：

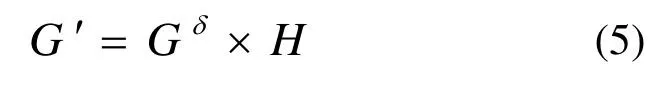
精细采样平衡解码算法的点扩散函数写成[6]：

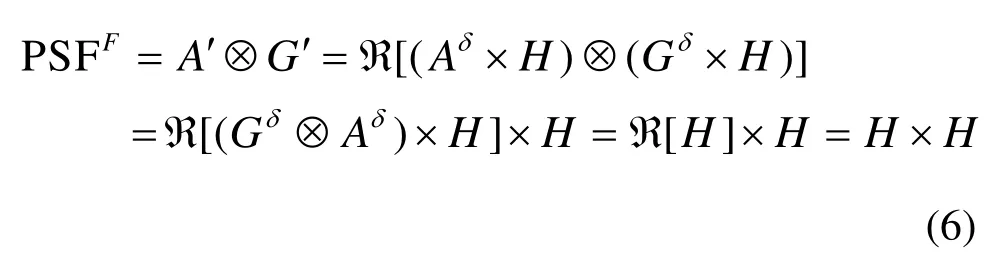
几何分辨率是编码孔径成像系统的一项重要指标，它的优劣直接影响到成像系统的定位精度。PSF也称为点源响应，当两个放射源之间的距离是PSF的半高宽(Full Width at Half Maximum, FWHM)时，认为这两个放射源刚好能够在重建图像中被分离开，因此将系统PSF的FWHM称为系统的几何分辨率。我们假设a=3对两种解码PSF进行对比分析，如图4所示[8]。两种解码的FWHM是一样的，按照几何分辨率的定义，可知两种解码算法所得重建图像的分辨率应该是一致的。但是比较式(5)和(6)可知，精细采样解码算法的PSF可以看出是从δ解码算法的PSF与H卷积得到的，相当于对δ解码算法的PSF做了一次低通滤波。所以推断出，精细采样平衡解码算法所得的结果应当比δ解码算法重建结果更加清晰。

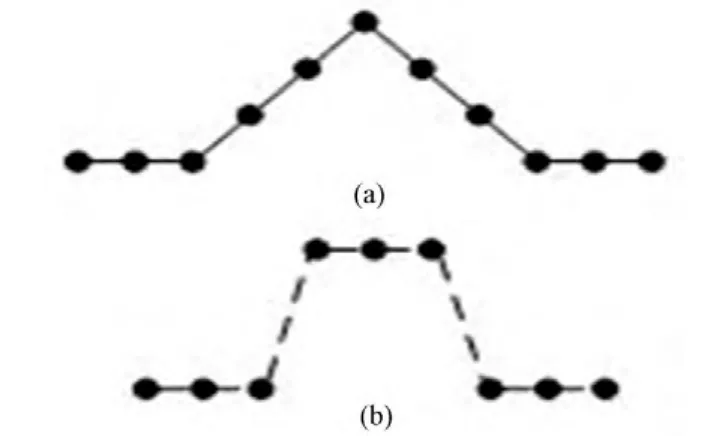
图4 两种解码算法的PSF比较Fig.4 Comparison of PSFs of two decoding algorithms.

2 近场成像的数据矫正

图5为编码孔径成像的几何示意图，放射源、编码孔准直器与探测器平面相互平行，放射源到编码板的距离为a，编码板到探测器的距离为b，一般将b作为系统焦距。用表示放射源的强度，表示探测器上位置处的粒子计数，它可以表示成[9]：

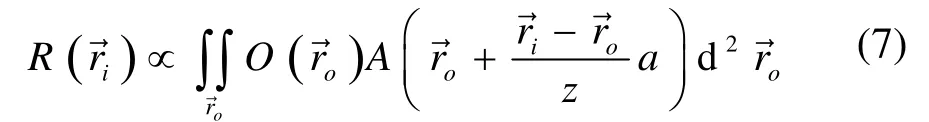
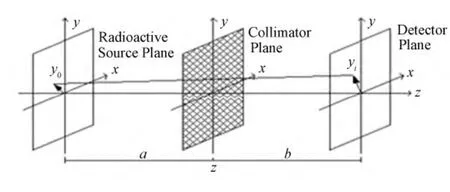
图5 编码孔径成像系统几何示意图Fig.5 Schematic diagram of the geometry of coded aperture imaging system.

其中：

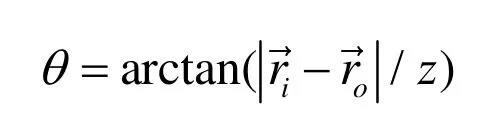
因为z=a+b，记是放射源平面上的位置矢量经过编码孔中心后在探测器上的投影矢量。

设定

则式(8)还可表示成：

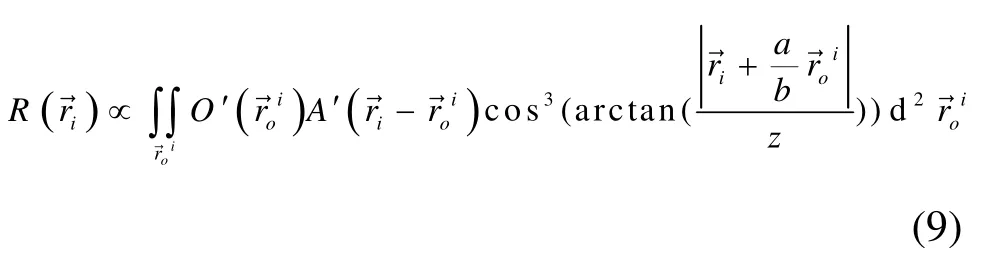
3 实验测试

仿真过程在探测器理想投影的基础上，让投影的每个像素与一个二维高斯分布进行卷积运算，高斯分布标准差是探测器几何分辨率的倍[10]；而成像系统的噪声则采用泊松噪声来近似处理[11]。系统其它参数统一设置为：放射源到准直器的距离a=100 cm，准直器到探测器距离b=4.69 cm；准直器采用嵌套 MURA 37×37，小孔大小pm=0.18cm。

3.1 两种算法的比较

根据前期两种算法的仿真实验[11]，假设探测器具有理想几何分辨率，在视场中心放置直径为3mm，活度为1.11×109Bq的241Am。模拟计数时间为60 s，采样数a=15。不加噪声时，精细采样平衡解码算法与δ解码算法重建图像的清晰度基本相同，如图6(a)、(b)所示。加入泊松噪声后，两种解码算法的重建图像都能清晰分辨出放射源亮点，见图6(c)、(d)，但是δ解码算法的重建图中含有“颗粒状”噪声。分别计算两幅图像的对比度-噪声比(Contrast to Noise Ratio, CNR)[12−14]：

计算得出图6(c)、(d)的CNR分别为113.93和38.08，表明在有噪声时精细采样算法所得的重建图像质量要好。

图6 无噪声时精细采样解码(a)、δ解码所得图像(b)和有噪声时精细采样解码(c)、δ解码(d)所得图像Fig.6 Reconstructed images using two decoding algorithms.(a) δ decoding without noise, (b) FSBD decoding without noise, (c) δ decoding with noise, (d) FSBD with noise

3.2 成像系统测试重建

3.2.1 单点源成像测试

在视场中放置一个直径为 3 mm、活度为3.7×108Bq的99Tc。采集计数500 K，分别放于视场中心和视场(Field of View, FOV)角q=20°时进行测试，实验结果如图7所示，图7(a)、(d)为探测器投影图，图7 (b)、(e)为精细平衡采样法重建平面图，图7 (c)、(f)为三维图。

实验结果表明，系统可以对单个点源在视场角q=20°的范围内清晰成像并重建。

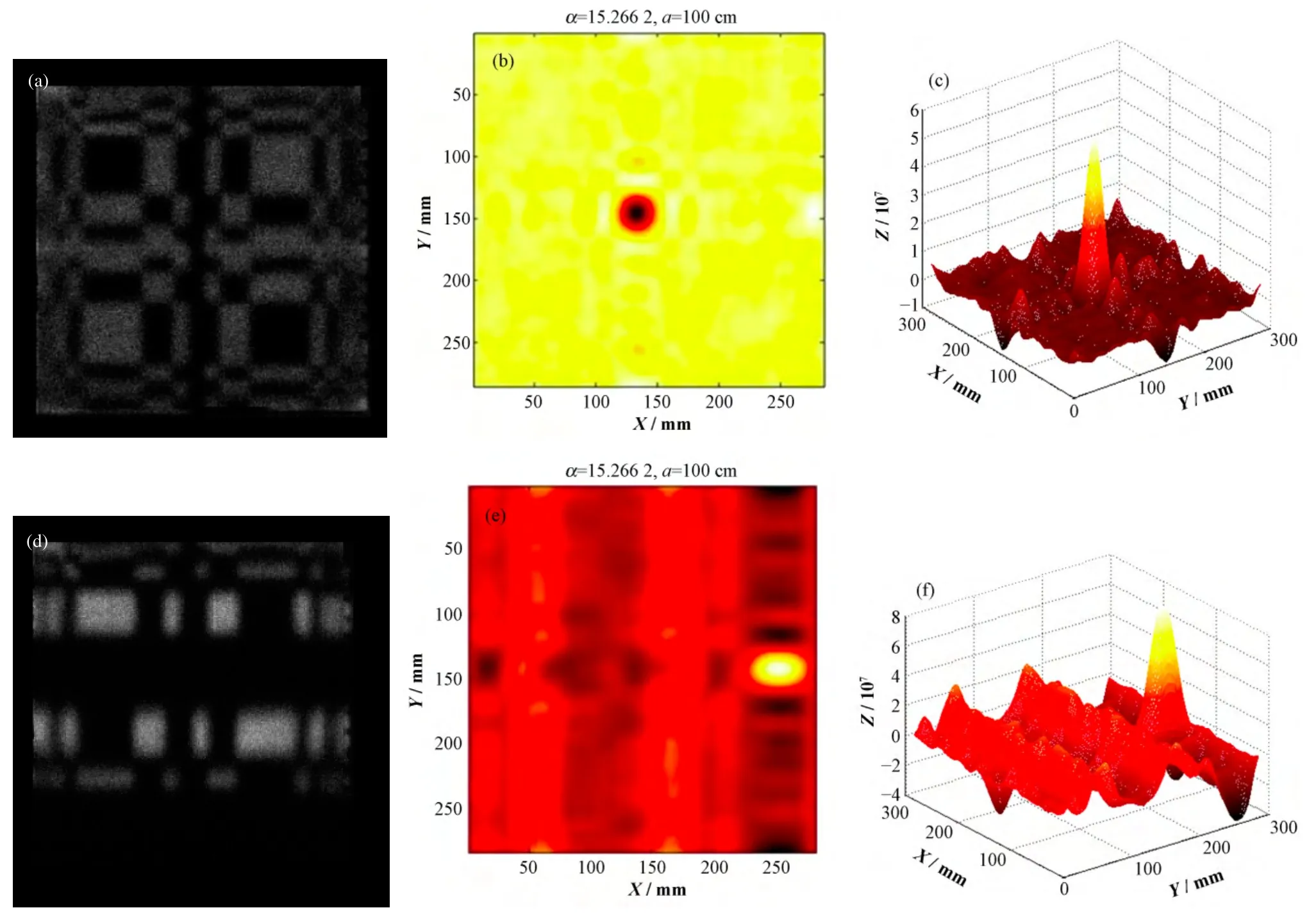
图7 视场中心单点源的探测器投影(a)、重建图(b)三维投影(c)和视场角q=20°时单点源的探测器投影(d)、重建图(e)、三维投影(f)Fig.7 Detector projection of one single point source at center of FOV (a), the reconstructed image (b), 3D projection image (c), and single point source at FOV angle of q=20° (d), the reconstructed image (e), 3D projection image (f).

3.2.2 两个点源成像

将两个直径为 3 mm、活度为 1.11×109Bq的241Am放置于同一平面上，一个点源距视场中心距离为15cm，视场角θ=arctan(15/104.69)=8.15°；另一个点源距视场中心距离为 25 cm，视场角θ=arctan(25/104.69)=13.43°，采集计数500 K。结果如图8所示。图8(a)为探测器投影图，图8 (b)与(c)分别为精细平衡采样法重建平面图与三维图，图8(d)和(e)分别为δ解码重建的平面图与三维图。

重建结果显示，成像系统不仅清晰分辨出两个亮点，而且如实体现了两个放射源之间的距离，说明系统对两个点源的重建是可行的，同时也验证了仿真实验中精细平衡采样算法重建优于δ解码重建算法的推理。

4 结语

在基于 MURA编码孔径准直器成像系统的解码过程中，在MATLAB环境下对δ解码算法和精细采样平衡解码算法进行了编程实现，并对其在图像重建质量方面进行了对比研究。在仿真实验结果基础上，对单点源和双点源在 20°视场角内进行实验测试，将所得的投影图像进行重建。实验结果表明，成像系统能够对单个点源或两个点源进行清晰成像，并且能真实反映放射源的位置信息，在有噪声的仿真实验和实验室实际测试中，精细平衡采样算法重建效果均优于δ解码重建算法。

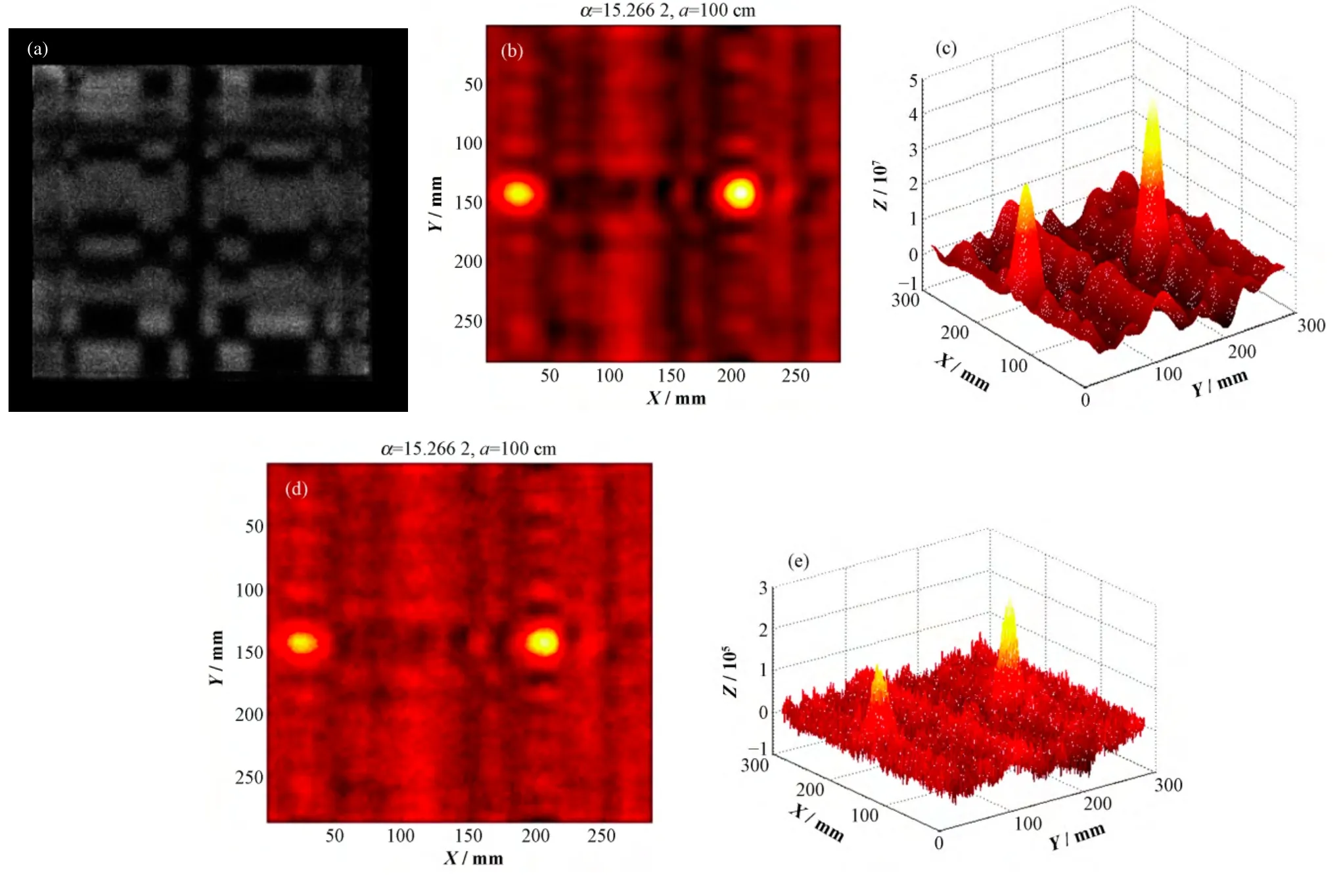
图8 双点源的探测器投影(a)以及两种算法的重建图(b、d)与三维投影(c、e)Fig.8 Detector projection of two point sources (a) and the reconstructed images (b, d) and 3D projection images (c, e) of two decoding algorithms.

1 Mert L, Young N O. Fresnel transformation of images[A].Proceedings of the international conference on optical instrumentation and techniques[C]. London: Chapman and Hall, 1961: 305−310

2 Fenimore E E, Cannon T M. Coded aperture imaging with uniformly redundant arrays[J]. Applied Optics, 1978,17(22): 337−347

3 洪俊杰, 戎军艳, 王人松, 等. 近场编码孔径成像的数据校正[J]. 核电子学与探测技术, 2007, 27(4): 764−767 HONG Junjie, RONG Junyan, WANG Rensong,et al.Data correction for coded aperture in the near-field imaging[J]. Nuclear Electronics & Detection Technology,2007, 27(4): 764−767

4 Zhao C L, Li Y P, Chen L H,et al. The experimental study of Lanthanum Bromide detector in the gamma ray imaging[J]. Applied Mechanics and Materials, 2013,336−338: 373−378

5 陈立宏, 李勇平, 赵翠兰, 等. 基于MURA编码孔径准直器核辐射成像系统的设计[J]. 核技术, 2013, 36(8):080402 CHEN Lihong, LI Yongping, ZHAO Cuilan,et al. Design of nuclear imaging system based on MURA coded aperture collimator[J]. Nuclear Techniques, 2013, 36(8):080402

6 Accorsi R. Design of near-field coded aperture cameras for high-resolution medical and industrial gamma-ray imaging[D]. PhD Thesis. Massachusetts Institute of Technology, 2001

7 Fenimore E E, Cannon T M. Uniformly redundant arrays:digital reconstruction methods[J]. Applied Optics, 1881,20(10): 1858−1864

8 Accorsi R, Lanza R C. Near field artifact reduction in planar coded aperture imaging[J]. Applied Optics, 2001,40(26): 4697−4705

9 Charalambous P M, Dean A J, Stephen J B,et al.Aberrations in gamma-ray coded aperture imaging[J].Applied Optics, 1984, 23(22): 4118−4123

10 陈立宏. 基于MURA准直器核辐射成像成像系统研究[D]. 硕士学位论文. 中国科学院大学, 2013 CHEN Lihong, Study of nuclear imaging system based on MURA coded aperture collimator[D]. Master Thesis.University of Chinese Academy of Sciences, 2013

11 肖洒, 兰明聪, 党晓军, 等. MURA编码孔成像中g分布的数值重建[J]. 核电子学与探测技术, 2013, 8(33):913−918 XIAO Sa, LAN Mingcong, DANG Xiaojun,et al. Digital reconstruction of g-source distribution in MURA coded aperture imaging[J]. Nuclear Electronics & Detection Technology, 2013, 8(33): 913−918

12 高艳. 单光子成像理论与实现[D]. 硕士论文. 浙江大学, 2002 GAO Yan. Single photon imaging theory and implementation[D]. Master Thesis. Zhejiang University,2002

13 Baydush A H, Floyd C E Jr. Bayesian image estimation of digital chest radiography: interdependence of noise resolution, and scatter fraction[J]. Medical Physics, 1995,22(8): 1255−1261

14 Mu Z P, Liu Y H. Aperture collimation correction and maximum-likelihood image reconstruction for near-field coded aperture imaging of single photon emission computerized tomography[J]. IEEE Transactions on Medical Imaging, 2006, 25(6): 701−711