叠前弹性参数反演方法的关键技术

邢小林， 石 颖， 方修政， 李婷婷， 曾 科

(东北石油大学 地球科学学院，黑龙江 大庆 163318)

0 引言

近年来，随着中国陆上含油气盆地勘探开发技术日趋成熟，油气勘探的主要目标已转向岩性和隐蔽性油气藏。作为岩性油气勘探重要环节之一，储层预测与描述有了长足发展[1]。储层预测技术是以地震反演为核心的。以叠后数据为基础的地震反演在油气勘探中起到了重要作用。但处理时采用全角度多次叠加后地震资料进行叠后反演，缺乏叠前数据体所包含的振幅和旅行时信息，这在一定程度上削弱了部分储层特征的敏感性。另外，叠后地震数据反演未能给出泊松比、纵横波速度比等反映物性、流体特征的参数，限制了对储层物性、流体特征的研究。随着勘探开发难度的不断加大，使用叠后地震储层预测技术来完成岩性地层油气藏勘探的任务越来越困难，于是学者们将研究目标由叠后地震数据转移到叠前地震数据的分析和应用方面。

AVO(Amplitude Versus Offset)技术出现于20世纪80年代，该技术很大程度上提高了地震烃类的检测能力。随着勘探目标的日益复杂化和计算机技术的快速发展，叠前偏移技术在解决复杂成像问题中发挥了重要作用[2]。近年来，叠前时间偏移和AVO技术相结合的叠前弹性参数反演方法得到了越来越多的重视[3]。Connolly[4]提出了类似于声波阻抗的且与入射角有关的弹性阻抗反演方法，将波阻抗的概念推广到非零入射角。马劲风[5]提出了广义波阻抗的概念，与原有方法相比，广义波阻抗反演的计算精度更高。甘利灯等[6]将弹性阻抗应用于岩体和流体预测方面，并给出了理论和实际数据的算例，认为在特定入射角的条件下弹性阻抗反演可以更好地识别岩性和流体。上述研究仅关注了弹性阻抗，但实际上弹性参数数量较多。弹性参数反演的理论基础是Zoeppritz方程，但该方程求解十分困难，故众多学者对其方程近似式进行了研究[7]。Zoeppritz方程近似式的求解相对简单，推进了叠前反演在实际地震资料中的应用，故Zoeppritz方程近似式研究十分重要。

笔者分析几种Zoeppritz方程的近似式，并利用射线追踪的方法提取角度道集，然后根据实际情况选择合适的方程近似式对角度道集进行反演，以提高叠前反演算法的精度。

1 叠前弹性参数反演基本原理

假设二维介质是由被平界面分开的两层均匀介质的固体地层构成的，如图1所示。介质1中的纵波与横波的速度分别为vp1和vs1，介质密度为ρ1;介质2中纵波和横波速度为vp2和 vs2，介质密度为 ρ2;φ0为纵波入射角;φ1和 φ2分别为纵波反射角与透射角;θ1和θ2分别为横波反射角与透射角。

图1 Zoeppritz方程的介质模型及其与波的关系Fig.1 Relationship between medium of Zoeppritz equation and wave

采用Officer提出的关于反射波与透射波振幅的方法推导Zoeppritz方程，可得以下由矩阵形式表示的 Zoeppritz方程[8]:

式中:Rpp、Rps——反射纵波与反射横波的反射系数;

Tpp、Tps——透射纵波与透射横波的透射系数。

式(1)给出了由反射角和透射角表示的平面波反射系数与透射系数、弹性参数之间的关系。

2 Zoeppritz方程近似式优选

2.1 Zoeppritz方程近似式

Zoeppritz方程是一个复杂的非线性方程，在实际应用中大多采用其近似式将非线性问题线性化，这样反射振幅与岩心和流体的关系就变得简单而又易于理解，运算速度快，反演相对容易。

2.1.1 Shuey近似式

Zoeppritz方程Shuey近似式为

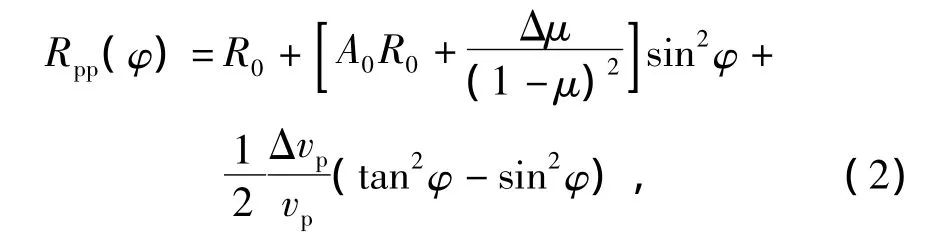
式中:R0——法向入射的反射系数;

A0——法向入射振幅;

μ——泊松比;

φ——入射角。

式(2)中各参数计算式为:

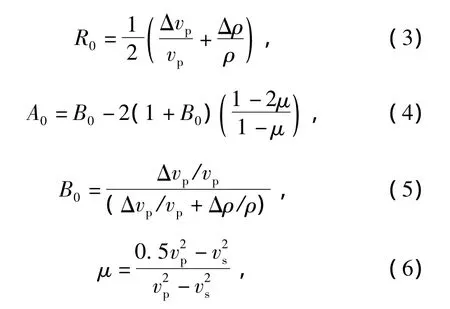
由Shuey近似式可见，反射系数由三部分组成，第一项为法向入射项，第二项为小入射角项，第三项为大入射角项。当入射角较小时(φ＜30°)，式(2)的第三项往往可忽略。

2.1.2 Aki-Richards近似式

Aki-Richards给出的纵波反射系数近似式[9]为

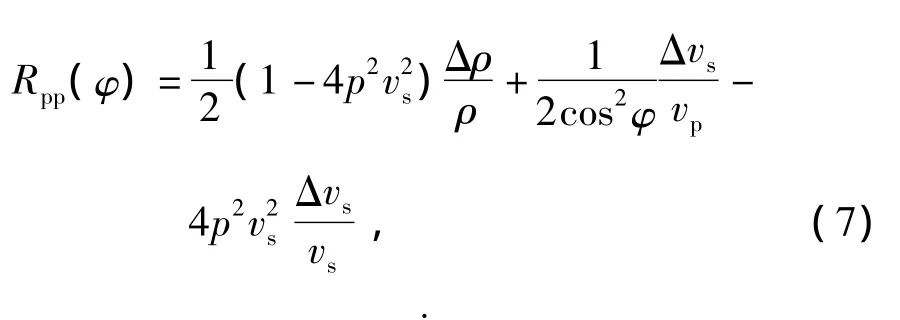
v——层速度。

式(7)的适用条件是假设反射界面两侧介质的弹性参数变化很小，满足:

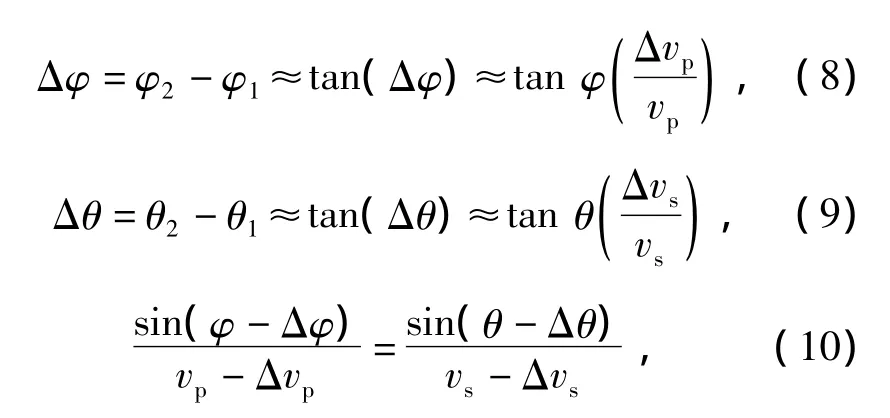
2.1.3 其他近似式

在Shuey公式和Aki-Richards近似式的基础上，很多学者提出了各种求解弹性参数的反演近似式，如 Smith-Gidlow 近似式[10]、Fatti近似式[11]、Gray近似式[12]以及 Xu-Bancroft近似式[13]。其中，Fatti近似式将反射系数与波阻抗的关系进一步简化，Gray以及Xu-Bancroft近似式则是反演计算拉梅系数的近似公式。

2.2 计算精度对比

设计地质模型，采用上述近似式试算纵波反射系数，并与Zoeppritz理论方程进行精度对比。在临界角以内，近似式的计算精度很高，所以在入射角不大的情况下，可以采用适合的近似计算式来求解所需弹性参数[14]。

设计如图1所示的两层介质模型。图2a的模型弹性参数为:纵波速度 vp1=3 336 m/s，vs1=1 970 m/s，vp2=3 791 m/s，vs2=2 273 m/s，密度ρ1=2.4 g/m3，ρ2=2.6 g/m3;图 2b 的模型弹性参数为:纵波速度 vp1=3 000 m/s，vs1=1 800 m/s，vp2=3 500 m/s，vs2=1 900 m/s，密度 ρ1=2.3 g/m3，ρ2=2.5 g/m3。

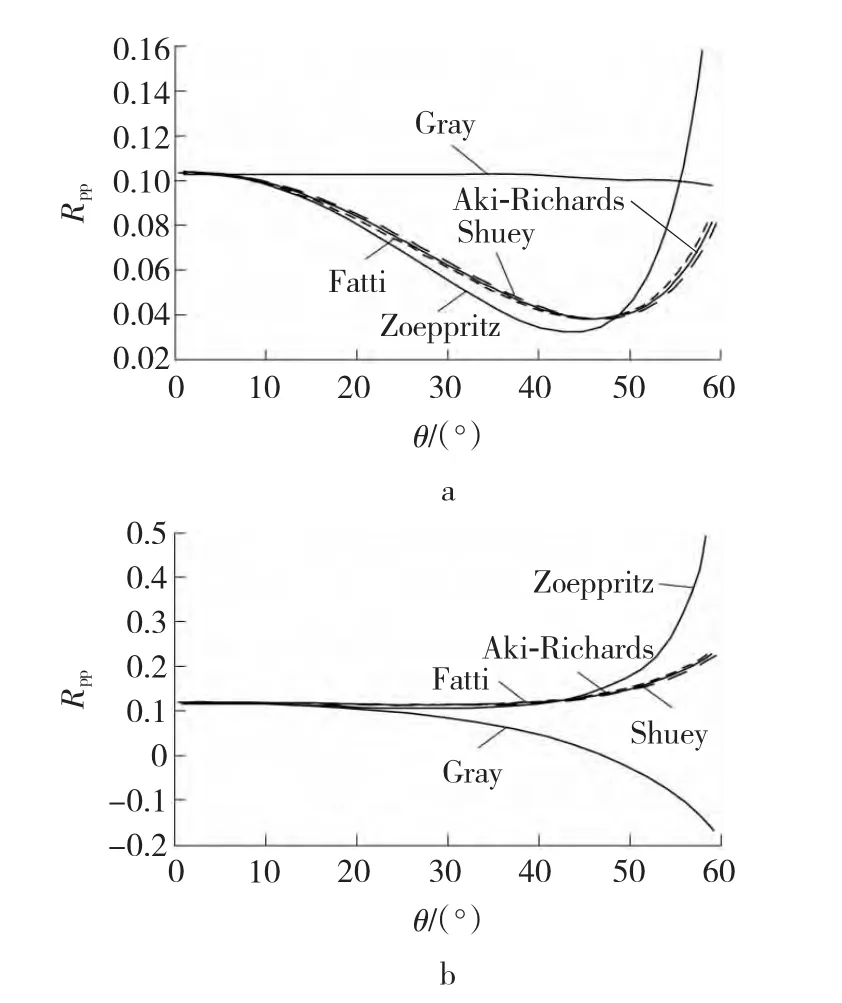
图2 Zoeppritz方程与其近似式计算精度对比Fig.2 Contrastive precision accuracy between Zoeppritz equation and its approximation equation

从图2a可看出，在临界角范围内，图中所示的介质符合近似式的假设，界面两侧的弹性参数变化率不大，Shuey近似式、Fatti近似式、Aki-Richards近似式在临界角内与Zoeppritz理论方程计算的纵波反射系数基本一致，不过当入射角大于50°时，开始有明显偏差。而Gray近似式在大于15°时，就已经有明显偏差，说明此近似式当前介质模型计算精度很低，故在计算反射系数时，不采用此种近似式。图2b中，入射角大于25°时，Gray近似式相对于Shuey近似式的偏差就开始逐渐增大。虽然Gray近似式能够反演求取拉梅系数，但一般入射角大于25°时，该近似式的反演计算偏差是很大的，这在一定程度上限制了该公式的应用。

实际应用中，所有的弹性参数均能通过反演得到，但对于不同的研究区块，需进行弹性参数敏感性分析，选取适合的近似式进行反演计算，以便应用有效的弹性参数进行储层预测和油气检测。

3 叠前参数反演的关键技术

3.1 无拉伸动校正技术

实际地震勘探中，从数据采集到数据处理，炮检距的函数均是由反射振幅描述的[15]。而Zoeppritz方程及其近似式均将入射角作为变量描述，因此，需要将振幅和炮检距的关系转换成振幅与入射角的关系，形成角度道集，以方便计算[16]。

实际的地震数据需要先进行动校正，然后抽角度道集。文中采用正演模拟水平层状介质得到地震记录，然后对得到的地震记录进行动校正，再对处理好的地震记录进行角度道集抽取。图3为层状速度理论模型，其深度(h)为3 000 m，由浅到深每层厚度分别为 350、150、250、100、150、2 000 m。纵波速度分别为 2 000、2 100 、2 300、2 500、2 700、3 000 m/s，密度分别为 2 000、2 100、2 300、2 500、2 700、3 000 kg/m3。图 4 为正演模拟的地震记录及其动校正效果。

图3 层状速度模型Fig.3 Model of layered velocity

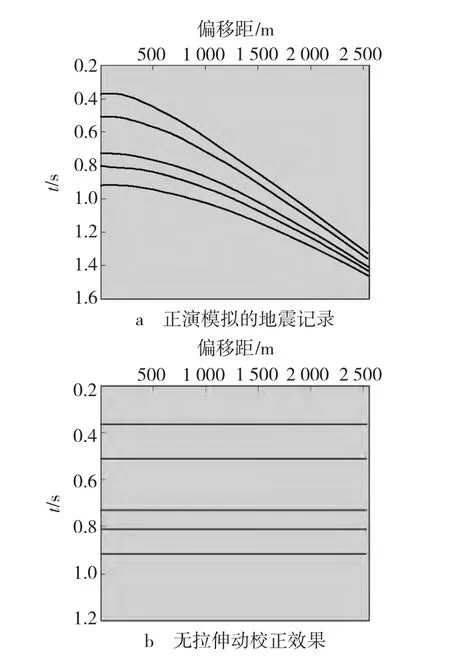
图4 正演模拟的地震记录及无拉伸动校正效果Fig.4 Seismic record of forward modeling and effect of no stretch NMO correction

3.2 角度道集抽取技术

3.2.1 射线追踪法抽取角度道集

角度道集是相对于一个CDP道集而言的，通过不同方法计算可以得到某一角度的出射地震波记录。角度道集有多种提取方法，主要依据波动理论和射线理论[17]。波动方法通过解波动方程生成角度域共成像点道集，这种方法主要用于速度分析。射线理论利用每个地震记录道上炮检距在不同时刻与反射角的关系，求取某固定角度的入射振幅。由于射线理论的角度道集提取方法速度快、物理意义明显，因此，在地质情况较简单时是普遍采用的方法。

角度道集抽取方法很多，文中选用射线追踪法，即利用均方根速度求取层速度进行角道集抽取。如图5所示，基于水平层状介质的假设，下行波和上行波的传播路线都是直线。

图5 均匀介质中地震波的传播路径Fig.5 Propagation path of seismic wave in homogeneous medium

在这种情况下利用三角关系可知

式中:x——炮检距。

如已知目的层的层速度，则炮检距与入射角的关系为

式中:t0——零炮检距双程旅行时。

为了方便分析，采用Shuey近似式中入射角的表达式，将式(12)转换成用sin2φ表达的形式，即

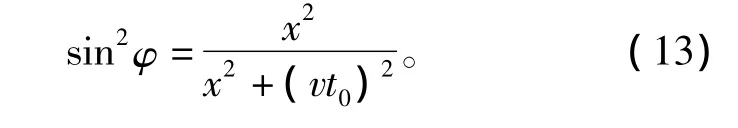
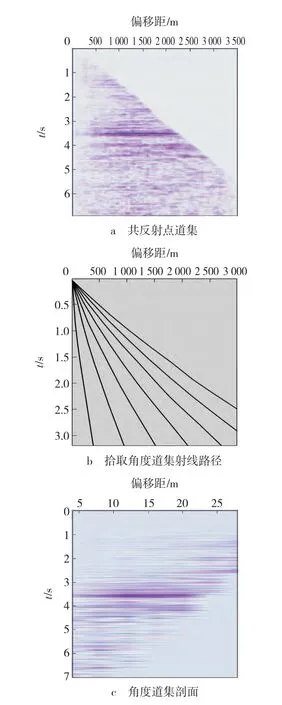
图6 实际资料角度道集抽取Fig.6 Actual data angle gathers extraction

3.2.2 角度道集抽取效果

应用射线参数法对实际地震数据进行角度道集拾取，所处理的地震数据为某凹陷的一条主测线进行Kirchhoff叠前时间偏移后形成的共反射点道集。任意抽取一条CRP道集，如图6a所示。根据该道集的叠加速度信息计算得到角度道集射线，如图6b所示，所形成的角度道集剖面如图6c所示。很显然，角度道集的倒数比CRP道集少，但信噪比高。对实际采集的工区进行逐个CRP道集运算就能得到所有的角度道集数据。

4 理论反演应用测试

理论计算所用地层模型为图3所示的速度模型，利用Fatti给出的Zoeppritz近似方程对其进行理论试算。假定纵波速度为横波速度的两倍，利用最小平方法求解超定方程的方法。图7为利用Fatti方程反演的反演值与每层理论值的对比结果。计算结果表明，波阻抗的计算最大误差为4.90%，密度参数的最大误差为5.87%。该方法对波阻抗的计算误差较小，而受最大入射角的影响，密度参数计算的相对误差稍大一些，但仍在工业生产允许的范围内。因此，文中给出的弹性参数反演方法对实际地震资料的反演计算具有一定的适应性。

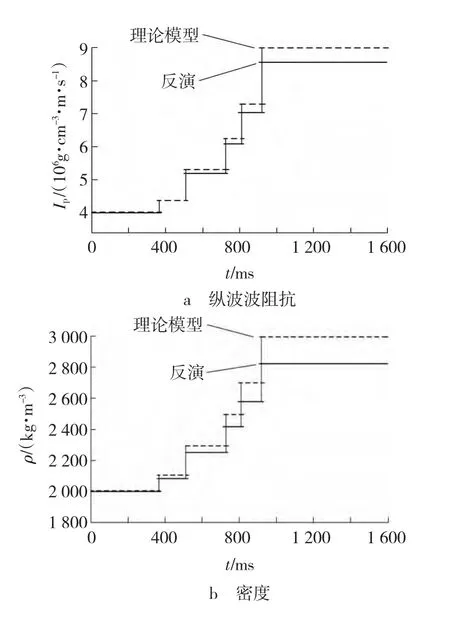
图7 纵波波阻抗及密度反演对比Fig.7 Correlation between longitudinal wave impedance and density inversion

5 结束语

研究叠前弹性参数反演及关键技术，并进行理论模型的试算。试算结果表明，叠前弹性参数反演方法在一定程度上可以提高储层预测精度。对于地质区域、研究目的不同的情况，可以采用不同的Zoeppritz方程近似式求解不同的弹性参数。不同的弹性参数可以组合预测储层。文中给出的叠前反演方法具有很强的实用性，对于油气藏的勘探具有一定应用价值。

[1]贾承造，赵文智，邹才能，等.岩性地层油气藏勘探研究的两项核心技术[J].石油勘探与开发，2004，31(3):3－9.

[2]方伍宝.三维叠前深度偏移的建模技术[J].石油物探，2002，41(2):132－135.

[3]马淑芳，李振春.波动方程叠前深度偏移方法综述[J].勘探地球物理进展，2007，30(3):153－161.

[4]CONNOLLY P.Elastic impedance[J].The Leading Edge，1999，18(1):438－452.

[5]马劲风.地震勘探中广义弹性阻抗的正反演[J].地球物理学报，2003，46(1):118－124.

[6]甘利灯，赵邦六，杜文辉，等.弹性波阻抗在岩性和流体预测中的潜力分析[J].石油物探，2005，44(5):504－508.

[7]SHUEY R T.A simplification of the Zoeppritz equations[J].Geophysics，1985，50(4):609 －614.

[8]OFFICER C B.Introduction to the theory of sound transmission with application to the ocean[M].[S.l.]:McGraw-Hill Book Co，1958.

[9]AKI K，RICHARDS P G.Quantitative seismology[M].2nd.[S.l.]:University Science Books，2002.

[10]SMITH G C，GIDLOW P M.Weighted stacking for rock property estimation and detection of gas[J].Geophysics Prospecting，1987，35(9):993－1014.

[11]FATTI J L，SMITH G C，VAIL P J，et al.Detection of gas in standstone reservoirs using AVO analysis:a 3-D seismic case history using the Geostack technique[J].Geophysics，1994，59(9):1362－1376.

[12]GRAY D，GOODWAY B，CHEN T W.Bridging the gap:using AVO to detect changes in fundamental elastic constants[C]//1999 SEG Annual Meeting.Texas:Society of Exploration Geophysicists，1999:1456 －1458.

[13]XU Y，BANCROFT J C.Joint AVO analysis of PP and PS seismic data[R].[S.l.]:CREWES Research Report，1997，9:1－44.

[14]GARDNER G H，GANDNER L W，GREGORY A R.Formation velocity and density:the diagnostic basics for stratigraphic traps[J].Geophysics，1974，139(1):770 －780.

[15]葛文军.迭代曲射线法求角道集[J].石油地球物理勘探，1992，27(3):410－420.

[16]石殿祥.AVO分析中求角度道集新方法[J].石油地球物理勘探，1994(S1):10－19.

[17]张广智，王文龙，印兴耀，等.基于射线理论的角度道集提取方法综述[J].地球物理学进展，2011，26(5):1696－1707.