不同微造型的钻井泥浆泵缸套的有限元分析

张锟，郭占斌，李夺，吴立宏

（1.黑龙江八一农垦大学工程学院，大庆163319；2.大庆物探公司开发中心委内瑞拉项目部）

钻井泥浆泵是地质钻探的三大部件之一，是构成钻井液循环系统的关键设备，通过高压输送钻井泥浆而起到冲洗井底、携带岩屑、冷却钻头等作用。活塞和缸套是实现泥浆循环的关键部件，由于工况复杂、条件恶劣，活塞缸套摩擦副的使用寿命偏低[1]。因此，了解和研究缸套的应力分布和温度场情况，不但能提高缸套的使用寿命，而且有利于泥浆泵缸套的优化设计、制造及维修使用。对提高钻井作业的工作效率，节省经济支出有着十分重要的意义。通过表面微观结构的设计，如缸套工作表面加工的几何形态结构[2-4]，可以形成良好的油膜，从而可提高活塞-缸套摩擦副的润滑效果和耐磨性。

国内对此亦有一些相关的研究。2006年和2007年，江苏大学的符永宏等[5]采用激光微造型技术在发动机缸套内表面加工出了高质量表面微观几何形貌，在往复式活塞环-缸套摩擦磨损模拟试验机上进行了激光造型与未造型光滑缸套试件的摩擦磨损性能对比试验研究，证明了一定的表面粗糙度反而有利于润滑油膜的形成从而减小摩擦磨损。达到了改善其润滑状况，提高其润滑耐磨性能的目的。2009年吉林大学和中原油田等单位的高科等[6]，在分析仿生非光滑表面减阻、防黏和酎磨特性的基础上，将该理论引入到钻头设计中，研制高效率、耐磨和减阻的仿生金刚石钻头。2011年河北师范大学的王再宙等[7]分别对非光滑凹坑表面和光滑表面滑动磨损过程进行模拟分析，结果表明非光滑表面具有较好耐磨性。

研究的创新之处是利用了创新、开放的企业级CAE平台Altair HyperWorks和ABAQUS软件，用有限元的分析方法来研究不同微造型内表面的泥浆泵内缸套的应力及热负荷情况，进而达到研究耐磨性和使用寿命的目的。研究选用了三种泥浆泵缸套模型，一种为常用的普通光滑内表面缸套模型，其余两种分别为经过微造型处理后的凹槽内表面和圆形凹坑内表面缸套模型。两种微造型的尺寸参数如下：凹槽微造型的槽宽600μm，深度300μm，造型间距为5 mm；圆形凹坑微造型的直径600μm，深度300μm，造型的行列间距均为5 mm。由于三种泥浆泵内缸套只有内表面的微造型不同，其余如外形尺寸、材料特性、受力情况等均完全一致，因此进行有限元分析的条件设置与分析步骤也基本相同，可进行统一论述。在分别完成三维模型和有限元模型的建立后，分析相同工作条件下的三种缸套相同部位的应力分布情况和温度场情况，并分别在内套模型的相同位置选取目标节点采集详细数据，对结果进行对比分析从而得出相关结论。

1 有限元模型的建立

1.1 三维模型的简化与建立

利用Pro-e对所选用的三种泥浆泵缸套进行三维建模。在建立泥浆泵缸套的三维模型时，考虑到生成缸套的内表面微造型结构的计算量比较大，并且在后期有限元分析时也需要面对庞大的计算任务。由于缸套的结构比较对称，所以可以把完整的三维模型简化为轴对称模型，既省去了不必要的计算量又不影响计算的精度，提高计算和分析的效率。因此，在建立模型时作了相应的简化，以坐标Y轴作为轴向对称，x轴的方向作为缸套径向，z轴的方向作为周向，取1/10缸套圆周部分作为最终的三维模型。

1.2 理论数学模型

由于活塞环在缸套内运动摩擦产生的温度场是一个复杂的摩擦生热过程，涉及到接触非线性和热边界非线性。为了使计算和分析过程收敛，研究选择的温度场有限元分析的建模方法是将摩擦能作为表面热流输入，即在热传导微分方程中把摩擦能作为边界热流率和温度场控制方程的边界条件，从而在一定程度上降低了模型的非线性[8]。

在计算中对模型作如下假设：活塞在缸套内只做直线运动，不考虑其横向摆动；机械载荷暂只考虑缸套与活塞环之间的摩擦力，暂不考虑活塞环和缸套间的润滑；在数值计算时，一般假设零件为常物性，在某一时刻的导热为准稳态导热。则导热微分方程为[9]：

式中：ρ——材料密度；

c——材料比热容；

T——温度；

t——时间；

λ——材料的导热系数；

Φ——单位时间内单位体积中内热源生成热；

x、y、z——笛卡尔坐标分量。

活塞环与缸套的摩擦力可按如下公式进行计算：

式中：μ——摩擦系数，μ=0.1；

P——工作时的压强，P=25MPa；

A——活塞环与缸套内表面的接触面积，mm2；

其中原模型接触面积A1=1 482.325mm2，圆形凹坑内表面接触面积A2=1 467.369 mm2，凹槽内表面接触面积A3=1 322.444mm2。

假设在单位时间内，摩擦界面间产生的热量完全被摩擦副所吸收，热量以热流形式在摩擦副间分布，则接触表面产生的摩擦热量为：

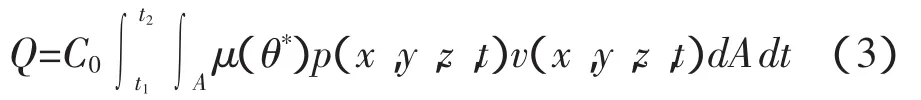
式中：C0——机械功的热当量；

μ——摩擦系数；

p——摩擦表面上的比压；

v——零件的相对移动速度；

A——接触面积；

t——时间；

θ*——为计算摩擦系数与磨损强度之间的温度关系时采用的特征温度。

假定摩擦副间的摩擦系数不随磨损和摩擦热的变化而变化，则由公式（3）可得输入到缸套的摩擦热流密度为[10]：

式中：FHTG——能量转化因子，FHTG=1；

FWGT——目标面和接触面间的热量分配权因子，FWGT=0.5；

μ——摩擦系数，μ=0.1；

P——工作时的压强，P=25MPa；

F——活塞环与缸套的摩擦力，N；

v——相对移动速度，v（t）=0.645m·s-1。

假设摩擦做的功全部转化为热量，故摩擦生热的能量转化因子为1。取热流分配因子FWGT为0.5，即热量平均分配到接触面上。

2 有限元网格划分与边界条件

2.1 网格划分及材料特性

将三维模型导入Hypermesh软件中进行合理的网格划分，为了达到较好的计算精度，对缸套微造型内表面的网格进行了细化。网格划分采用了手动划分的方式，在划分好面网格后再选中所有单元，完成体网格的生成。经过软件网格划分后，各模型对应得到的单元个数和节点个数如表1所示。

表1 各模型的单元数和节点数Table1 Number of elementand node in themodel

自定义材料的属性。所研究的双金属缸套的外套金属材料为45钢，内套金属材料为高铬铸铁，假定各材料密度均匀并且各向同性。在Hypermesh里的abaqus模板可查看材料的力学性能参数如下：45钢在20～204℃温度区间的比热容变化范围约为444～511 J·（kg·K）-1，温度在20～204℃区间时弹性模量变化范围为206～194GPa，密度为7.85×103 kg·m-3，泊松比为0.27。高铬铸铁在20～204℃温度区间的比热容变化范围约为510～590 J·（kg·K）-1，在20～204℃温度区间的弹性模量变化范围为209～196 GPa，密度约为7.8×103 kg·m-3，泊松比为0.3，屈服强度约为640MPa。

2.2 边界条件

由于几何模型较为简单，所以边界约束也并不复杂。内外缸套左右两截断面的约束条件为垂直于截断面平动，两个端面设置为三个轴向的位移边界约束。研究采用直接耦合的方法，先将摩擦力平均分配到摩擦力接触面节点上，然后通过公式（3）和公式（4）将计算得到的摩擦热流密度q作为体载荷分别施加在相应模型的热流载荷节点集上。根据泥浆泵工作情况，设置缸套承受压强的大小为25MPa，初始温度设置为20℃。缸套与活塞环的耦合条件为：q=q1+q2，令q1=q2=1/2q。q1代表缸套的热流密度，q2代表活塞环的热流密度。建立的有限元的模型如图1所示。

图1 原缸套、圆形凹坑内表面缸套和凹槽内表面缸套的有限元模型Fig.1 Finite elementmodel of the original，circular pits and fluted inner surface liners

3 计算结果及分析

3.1 应力场计算及结果分析

利用HyperWorks软件的Hyperview模块计算出相应的综合位移和应力分布情况。应力场分析得到了三组缸套在给定工况下的节点综合位移云图以及Mises等效应力分布图，如图2和图3所示。应力计算结果亦给出了节点的最大综合位移、最大主应力、最小主应力以及Mises等效应力。

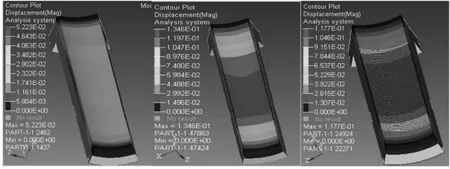
图2 原缸套、圆形凹坑内表面缸套和凹槽内表面缸套的节点综合位移云图Fig.2 Displacement cloud pictures of the original，circular pits and fluted inner surface liners

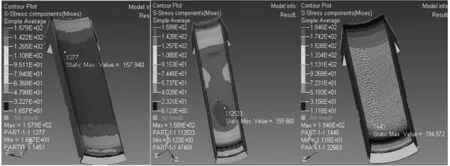
图3 原缸套、圆形凹坑内表面缸套和凹槽内表面缸套的M ises等效应力分布图Fig.2 Mises stress distributions of the original，circular pits and fluted inner surface liners

为进一步研究，分别在三组有限元模型上的相同位置等间距的选取了4个节点，共取12个节点，令相同位置的3个节点组成一个组，分别命名为A组、B组、C组和D组，然后在软件中计算出各节点的应力值。具体整理结果及各组节点的等效应力如表2和图4所示。

表2 选取的各节点ID及其分组Table2 Nodes ID and groups of the selected packet

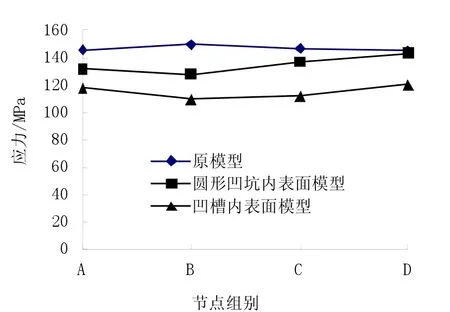
图4 各组节点的应力曲线Fig.4 Stress curve of the each nodes

由Mises等效应力分布云图和应力分析结果可以看出：在热负荷及压力综合的作用下三组缸套模型的最大应力分别为157.97 MPa、159.86 MPa和194.57 MPa，最大值均未超出材料屈服极限且满足安全工作的要求；等效应力较大处主要出现在缸套内表面的中间区域，等效应力由中间部分向两端逐渐减小，这是由于缸套受到流体的压力和负载逐渐增大，摩擦副间的磨损表面塑性变形严重，塑性变形功也相应增加[11]，摩擦接触产生了较大的热应力；圆形凹坑内表面和凹槽内表面缸套的应力分布比原模型要均匀。由图4可以看出，在相同工作条件下，模型上相同位置的节点应力与不同微造型表面之间的关系。原模型的各组相同位置的节点应力值最大，圆形凹坑内表面模型的各组节点应力值与原模型的相比要小些，而凹槽内表面模型的各组节点应力值为其中最小。

3.2 温度场计算及结果分析

利用HyperWorks软件的Hyperview模块直接计算出了相应模型微造型内表面的温度，并在后处理中以云图的形式显示出了温度场，如图5所示，各组节点的温度如图6所示。

图5 原缸套、圆形凹坑内表面缸套和凹槽内表面缸套的温度场分布图Fig.5 Temperature distributions of the original，circular pits and the fluted inner surface liners

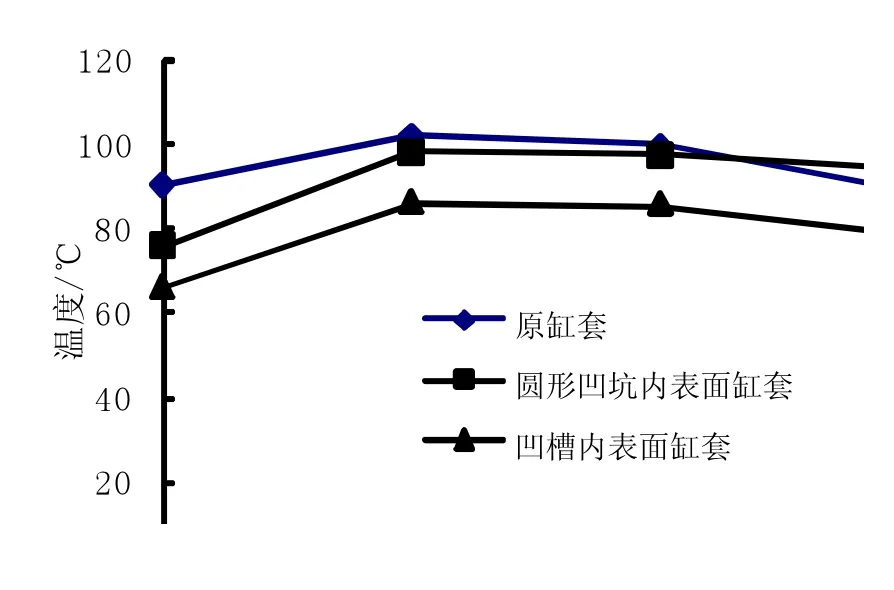
图6 各组节点的温度曲线Fig.6 Temperature curve of the each nodes

由图5和图6可以看出：三个模型的最高温度分别为105.51℃、103.6℃和88.94℃。由于缸套除受到流体的压力和摩擦接触产生的热应力，接触变形和应力逐渐增大，从而中部摩擦产生的热量也逐渐增加，温度较大处主要分布在内表面的中间区域，温度由中间部分向两端逐渐减小。

在相同的位置，原模型上节点的各温度值最大，圆形凹坑内表面模型上节点各温度值与原模型的相比要小些，而凹槽内表面模型上节点各温度值为其中最小。其中圆形凹坑内表面温度的分布差异有些大，圆形凹坑内表面和凹槽内表面缸套的温度变化和分布都要较原缸套理想，凹槽内表面缸套的温度梯度变化最为平缓，温度分布也最为均匀。

4 结论与讨论

通过建立有限元模型并采用有限元分析的方式，比较了不同微造型内表面的泥浆泵缸套在工作状况下的各项应力值及温度分布情况，得出了不同微造型表面与耐磨性的相关联系。工作应力和温度都是影响摩擦性能的重要因素，工作温度较低、从高温到低温降温速率的平稳或者温度分布均匀，这几种情况都会提升耐磨的性能。

通过研究可发现，选取的两种微造型表面与原表面的缸套相比，相同工况下所受到的等效应力较小，温度分布较为均匀，其他应力和应变情况也较为理想。因此经过内表面微造型的泥浆泵缸套的耐磨性能要略优于未经过微造型的缸套，今后在设计时可以对泥浆泵缸套内表面进行优化改进，从而提高其耐磨损性能。

[1]苑惠娟，郭建英，苏子美，等.国产钻井泥浆泵活塞缸套摩擦副可靠性研究[J].中国机械工程，2013，24（11）：1425-1430

[2]张云电，叶雪明.表面微坑加工方法及装置：中国，ZL98115377.1[P].1998-07-03.

[3]张云电.蜂窝状微坑设计和制造技术[M].北京：科学出版社，2004.

[4]王国林，陈秉聪，任露泉.波纹型推土阻力的有限元分析[J].农业工程学报，1994，22（3）：34-39.

[5]符永宏，陆华才，华希俊，等.激光微珩磨缸套润滑耐磨性能理论分析[J].内燃机学报，2006，24（6）：563.

[6]高科，孙友宏，高润峰，等.仿生非光滑理论在钻井工程中的应用与前景[J].石油勘探与开发，2009，36（4）：519.

[7]王再宙，张春香，郑淑芝，等.仿生非光滑凹坑表面模型建立及仿真研究[J].机床与液压，2011，39（1）：92.

[8]孙睿珩，徐涛，左文杰，等.表面凹坑对活塞-缸套摩擦生热过程的影响[J].吉林大学学报：工学版，2009，39（5）：1235.

[9]荆碧舟，韩振南.缸套—活塞组耦合传热的有限元分析[J].中国农机化学报，2013，34（4）：184-186.

[10]徐宇.凹坑型仿生非光滑表面的热结构分析及耐磨性的机理研究[D].大连：大连理工大学，2009.

[11]郭占斌，高松林.油润滑条件下几种金属材料摩擦磨损规律研究[J].黑龙江八一农垦大学学报，2013，25（1）：19-23.