利用AMM I模型分析寒地水稻区试品种产量的基因型与环境互作

李红宇，任淑娟，魏玉光，刘梦红，潘世驹，赵洋，蔡永胜，郑桂萍，刘丽华

（1.黑龙江八一农垦大学农学院，大庆163319；2.黑龙江省八五六农场；3.黑龙江省大兴农场）

水稻品种区域试验目的在于测验新选育品系的稳定性、丰产性和地区适应性[1]。当前，品种间丰产性的比较使用常规的方差分析方法进行多重比较即可，而品种的适应性和稳定性则主要取决于基因型与环境的互作效应。1938年Yates和Cochran提出利用回归分析法分析基因型×环境互作以来，科研工作者使用多种方法研究基因型与环境的互作效应[2]。线性模型通常只能解释很少一部分交互作用，无法充分利用试验所获得的信息，约束性很大[3]。采用主效可加互作可乘模型（AMMI）对区域试验品系进行稳定性分析[4]，以期能够更为全面的评价品种，更有效的利用基因型与环境互作的互作效应。

1 材料与方法

1.1 试验材料

使用2012年黑龙江省垦区第二积温带早熟组水稻区域试验数据。参试品种11个，试验点8个，参试品种和试验地点在黑龙江省垦区均具有代表性。试验品种（系）和地点及代码见表1。

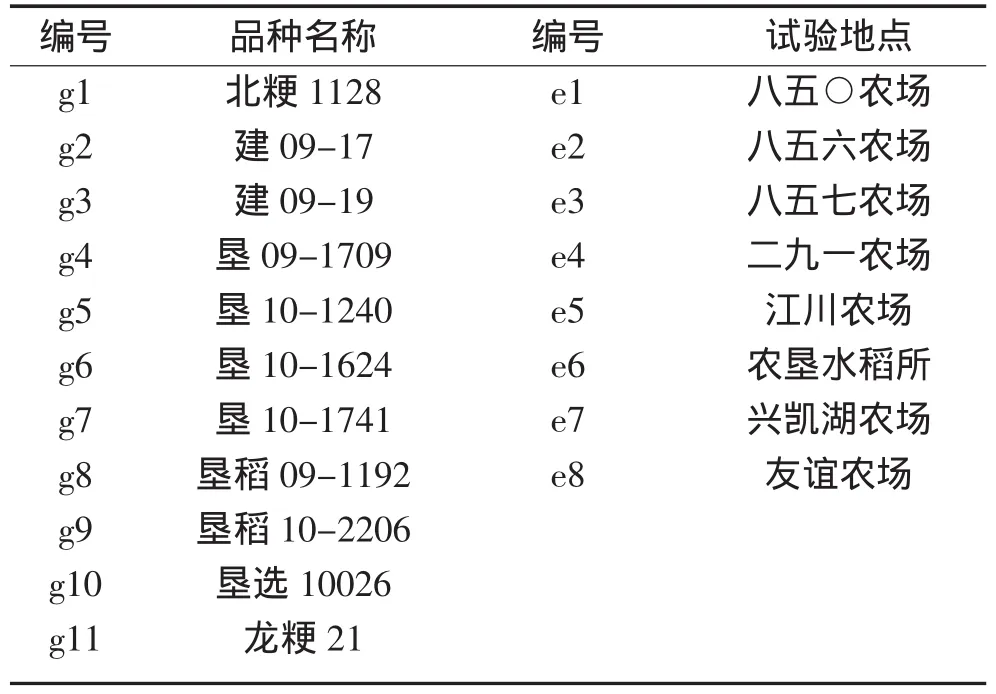
表1 参试品种及试验点Table1 Test varieties and sites

1.2 试验方法

1.2.1 试验设计

试验采用完全随机区组设计，三次重复，穴距和行距分别为12 cm和30 cm，施肥量和田间管理依据黑龙江垦区水稻区域试验方案进行。

1.2.2 统计方法

在基因型×环境互作效应显著的前提下，进行同质性检验和联合方差分析，采用主效可加互作可乘模型（AMMI）进行品种稳定性分析。

式中，Yger表示第g个基因型在第e个环境中的第r次重复观察值，u表示总体平均值，αg表示基因型平均偏差，βe表示环境的平均偏差，λn表示第n个主成分的分析特征值，γgn表示第n个主成分基因型的主成分得分，δen表示第n个主成分的环境主成分得分，n表示模型主成分分析中主成分因子轴的总个数，θger表示误差。代表所估算的基因型×环境交互作用（G×E），λn0.5 rgn和λn0.5δen分别表示基因型G与环境E交互作用的第n个交互作用主成分（IPCAn）。在所有显著的IPCA上，数值较小的基因型（或环境）即为稳定的基因型（或环境）。因此，在IPCA双标图上，基因型（或环境）愈接近坐标原点越稳定[6]。

参照吴为人[7]的计算方法计算品种稳定性参数Di。Di是一个品种在交互作用主成分（IPCA）空间中的位置与原点的欧氏距离。

式中，n表示显著的IPCA个数，γin表示第i个基因型在第n个IPCA上的得分，ωn表示权重系数，即每个IPCA所解释的平方和占全部IPCA所解释的平方和的比例。用Di为所有基因型给出相应的定量指标，品种的Di值越小，其稳定性越好。

采用Microsoft Excel 2003进行数据整理，使用DPS 7.05进行模型分析。

2 结果与分析

2.1 基因型与环境互作的AMM I模型分析

表2和表3结果表明，试验中各个参试品种的平均产量在不同试验区表现出不同数值，说明水稻品种间产量的稳定性不同。平均产量以建09-17最高，垦稻09-1192次之，北粳1128最低。同一试验区品种间产量性状平均值不同，说明不同环境对水稻产量性状的影响不同。平均值以农垦所水稻最高，八五〇农场次之，八五七农场最低。

表2 同一品种在不同试验区的产量平均值Table2 Average yield of same varieties from different test sites

续表2同一品种在不同试验区的产量平均值Continued Table2 Average yield of same varieties from different test sites

表3 同一试验区不同品种的3个品质性状平均值Table3 Average yield of different varieties from same test sites

对各试验点数据误差方差进行同质性测验，误差方差同质，进而进行产量联合方差分析（表4）。利用基因型、环境及基因型×环境平方和占总平方和的百分比（即SS%）表示三者对产量性状的影响力。表3结果显示，交互作用对产量的影响最大，SS%为51.9%，其次为环境，38.1%，基因型最低，10.0%。产量在品种间、环境间差异及基因型与环境互作效应均达到极显著水平，故有必要利用AMMI模型对产量进行稳定性分析。

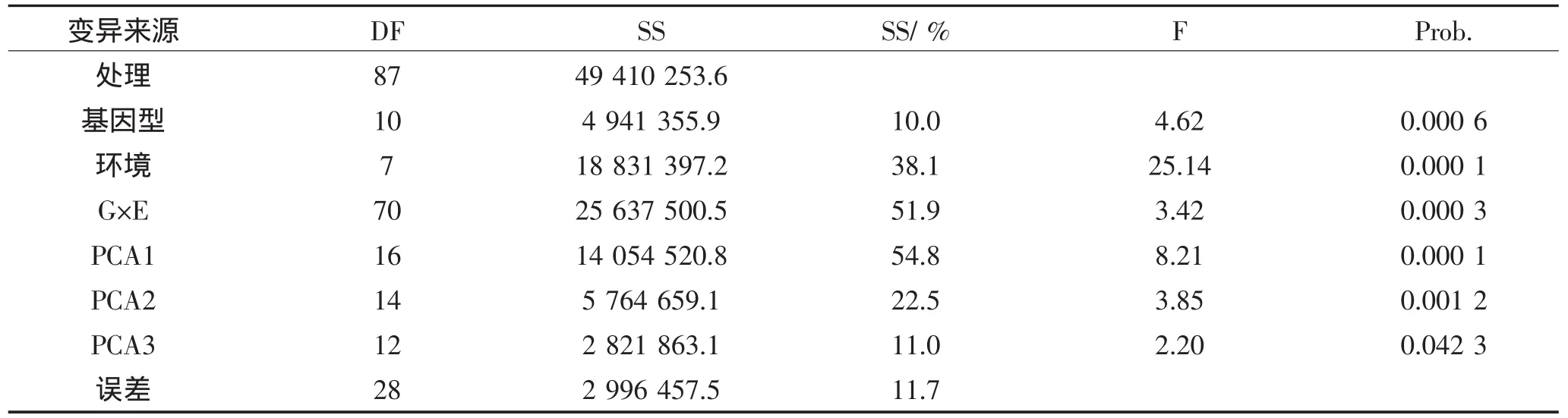
表4 参试品种的基因型和环境互作效应分析Table4 Analysis of the interaction of genotype and environment for rice yield

2.2 产量的稳定性及地点影响分析

AMMI模型稳定性分析结果显示（表4），产量主成分因子IPCA1、IPCA2和IPCA3的F测验显著或极显著，分别解释基因型×环境总变异平方和的54.8%、22.5%和11%。主成分因子IPCA1和IPCA2解释了基因型×环境总变异平方和的77.3%。因此，可以利用IPCA1和IPCA2代表的互作部分对产量稳定性进行评价。11个品种和8个生态点的主成分因子和相应稳定性参数Di值和Dj值列于表2和表3。11个参试材料稳定性以建09-19最好，其次是龙粳21，再次的是垦10-1240，稳定性最差的是垦稻10-2206。

以Dj值表示试验地点对品种产量的影响，D j值越大表示试验地点对品种产量影响越强，反之，影响越弱，影响强的地点更适宜作为区试地点。由表3可以看出，试验6个试点中，对产量影响最强的是二九一农场，其次是八五六农场，再次为八五〇农场，影响最差的为江川农场。

2.3 品种适应性分析

由于基因型×环境的IPCA1+IPCA2能够解释总变异的77.3%（表3），以IPCA1为横轴，IPCA2为纵轴制作AMMI双标图（图1），能够直观表示品种的稳定性和地点的影响力。在AMMI双标图上，以数据点距离坐标原点的距离表示品种的稳定性，距离越短，品种稳定性越好，距离越远，地点影响力越强。所以，双标图所反映出的品种稳定性和地点影响力与表2和表3结果相一致。

品种在某试点的最大交互效应用此地点图标与原点的连线在二维空间的垂直投影表示，其中于正向连线上的最大投影表示此品种在该试点表现出最佳适应性，若垂直投影在地点和原点的反向延长线上则表现出不适应性[8]。建09-17在八五〇农场和八五七农场，垦10-1624在八五六农场，垦稻10-2206在二九一农场和友谊农场，垦09-1709在江川农场、农垦水稻所和兴凯湖农场表现出最佳适应性。

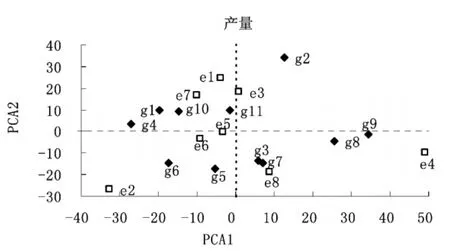
图1 品种产量的AMM I交互作用双标图Fig.1 AMMIbiplots（IPCA1-IPCA2）for yield of rice

3 结论与讨论

基因型×环境互作是一个复杂的生物学现象，要阐明其规律存在许多困难。AMMI模型集方差分析和主成分分析于一体，不但能够最大程度的反映基因型和环境互作效应，而且能够准确地描述品种的稳定性，是当前分析品种稳定性的最佳模型[9-12]。结果表明，基因型与环境互作对产量的影响最大，其次为环境，基因型最低。产量在基因型间、环境间差异及G×E互作效应均达到极显著水平，故利用AMMI模型对产量进行稳定性分析。IPCA1、IPCA2和IPCA3分别解释G×E总变异平方和的54.8%、22.5%和11%。参试材料稳定性最好的是建09-19，其次是龙粳21，再次是垦10-1240，稳定性最差的是垦稻10-2206；试验点中对产量鉴别力最强的是二九一农场，其次是八五六农场，再次为八五〇农场，最差的为江川农场。建09-17在八五〇农场和八五七农场，垦10-1624在八五六农场，垦稻10-2206在二九一农场和友谊农场，垦09-1709在江川农场、农垦水稻所和兴凯湖农场表现出最佳适应性。

[1]林国平，张俊杰，王毅，等.应用AMMI模型分析白肋烟品种的丰产性及稳产性[J].中国烟草科学，2009，30（4）：13-16.

[2]沈希宏，杨仕华，谢芙贤，等.水稻品种区域试验的品种×环境互作及其与气候因子的关系[J].中国水稻科学，2000，14（1）：31-36.

[3]董云，王毅，漆燕玲，等.应用AMMI模型分析评判甘肃省春油菜区试品种的稳定性和适应性[J].西北农业学报，2010，19（7）：74-78.

[4]宿飞飞，陈伊里，吕典秋，等.用AMMI模型分析马铃薯淀粉品质性状的稳定性[J].东北农业大学学报，2009，40（11）：18-22.

[5]苏振喜，赵国珍，廖新华.云南粳型特色软米食味品质性状稳定性分析[J].中国水稻科学，2010，24（3）：320-324.

[6]Piepho H P.Analyzing genotype-environment data by mixed models with multiplicative effects[J].Biometrics，1997，53：761-766.

[7]吴为人.对基于AMMI模型的品种稳定性分析方法的一点改进[J].遗传，2000，22（1）：31-32.

[8]刘丽华，胡远富，陈乔，等.利用AMMI模型分析寒地水稻3个品质性状的基因型与环境互作[J].作物学报，2013，39（10）：1849-1855.

[9]胡秉民，耿旭.作物稳定性分析[M].北京：科学出版社，1993.

[10]张泽，鲁成，向中怀.基于AMMI模型的品种稳定性分析[J].作物学报，1998，24（3）：304-306.

[11]樊龙江，胡秉民，许德信.水稻区域试验点对品种判别能力估算方法的研究[J].中国水稻科学，2000，14（1）：58-60.

[12]聂春阳，柴楠，杜春影，等.不同育苗方式对寒地水稻秧苗素质及产量的影响[J].黑龙江八一农垦大学学报，2012，24（3）：5-7.