输电线路的地线不平衡张力计算研究

杨晓梅 张瑞永 吴锁平

（1.江苏省电力公司，江苏 南京210024；2.江苏省电力设计院，江苏 南京211102）

0 引言

导地线架线时一般保持耐张段内各档纵向水平应力相同，受气温变化、不均匀覆冰和断线的作用，各档的应力将产生不同步变化，直线塔上会出现纵向不平衡张力，严重时会造成直线塔倒塔事故，极端条件下的气象、档距和高差组合将加剧这种不利影响。

根据文献［1—3］的研究结论，悬垂串串长越短、档距越大时，直线塔的覆冰不平衡张力越大，故对于特高压输电线路，地线的不平衡张力系数和发生事故概率要大于同条件的导线。对于中、重冰区，文献［4］给出了地线最大不平衡张力百分数的限值，但工程中杆塔是否超不平衡张力条件，还需通过验算确定。

由于覆冰不平衡张力的数学模型为高维非线性方程组，随着地线串长的减小，常规试凑法的计算精度急剧下降，10档以上计算精度几乎耗尽；文献［5］采用信赖域法求解不平衡张力问题，具有较强的鲁棒性，但该方法需求解高维Hessian矩阵，工程实现较困难。本文采用逐档提高迭代精度的方法求解地线覆冰不平衡张力问题，简单、收敛性好、计算精度高且便于软件实现。

1 覆冰不平衡张力及断线张力的计算模型

1.1 应力与档距增量的关系

假定耐张段内有n个连续档，考虑补偿初伸长而拉紧电线的水平应力为σ0、自重比载为γ0、架线气温为t0，采用斜抛物线表达的地线应力σi与档距增量Δli的关系式为［6］：

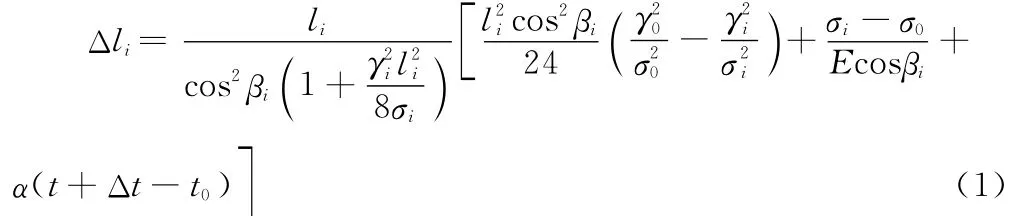
式中，li为第i档安装时的档距（m）；βi为高差角（°）；γi为张力不平衡时第i档比载［N／（mm2·m）］；E为弹性系数（N／mm2）；α为温度膨胀系数（1／℃）；t为张力不平衡时气温（℃）；Δt为考虑补偿初伸长降低的等效温度（℃）。

1.2 应力的显式方程

若不考虑悬垂串偏移引起地线悬挂点高差的变化，则根据第基直线塔上悬垂串顺线路的水平偏移可求出第i＋1档应力的显式方程［6］：

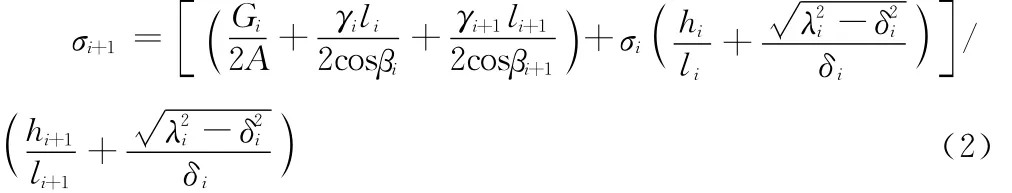
式中，A为地线的计算截面积（mm2）；Gi为悬垂串串重（N）；hi为第i基塔对第i－1基塔地线悬挂点的高差（m）；λi为悬垂串串长（m）。

1.3 不均匀覆冰及断线的求解条件

在整个耐张段内，不均匀覆冰时档距增量之和为0，即第n基塔上导线悬挂点的偏距为0：

而当第k＋1档地线断线后，地线分为2段：1～k档和k＋2～n档。如以1～k档的断线不平衡张力进行分析，第k基塔悬垂串承受k档的垂直荷载和纵向断线张力，此时有：

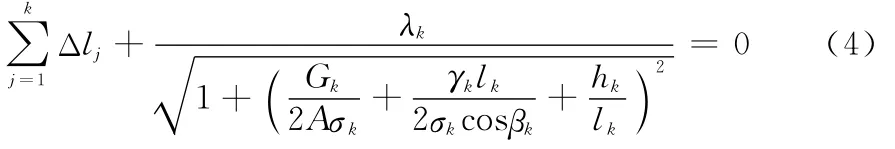
对于地线不均匀覆冰工况，分别以式（1）、（2）和（3）整理出2n个独立方程求解未知数σi和Δli；对于地线断线工况，可以式（1）、（2）和（4）整理出个2k独立方程求解1～k档的未知数σi和Δli。而对于k＋2～n档，可采用上述方法逆向求解。

2 逐档提高迭代精度的实现方法

2.1 计算方法

由于双精度浮点数仅可表示十进制的15或16位有效数字，而以式（2）采用试凑法求解地线不平衡张力时每次精度损失高达4～50倍，以致难以求出档数较多、串长较短的地线不平衡张力。采用逐档提高迭代精度的方法求解地线覆冰和断线不平衡张力的步骤如下：

（1）令试凑档l＝1，构造初值σ1、应力下限a、应力上限b：

（2）利用式（2）逐次由i档计算i＋1档应力，当｜δi＋1｜≥λi＋1时，利用二分法调整试凑档的初值σl、应力下限a、应力上限b，重新求解：

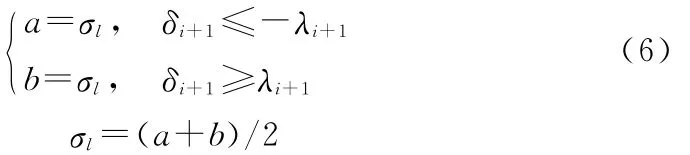
（3）当b≤a＋10eps时，表明试凑档已接近精度极限，需重新定义下一档为试凑档，设置误差阀值范围e，构造新试凑档的应力下限a、应力上限b，重复求解：

通过合理调整e值，可加快收敛速度、提高计算精度，一般可取e＝eps×105，此时应力的计算精度即为e。以上步骤循环求解，直至满足式（3）或式（4）。

2.2 稳定性验证

设耐张段含24档，地线采用LBGJ－170－20 AC铝包钢绞线，设计冰厚15 mm，档距取400 m，前12档覆冰率20%、后12档覆冰率100%，高差15%，串重取32.4 kg，张力误差阀值e取10－12，档距增量之和的误差阀值取10－7，地线采用不同串长时，普通试凑法与逐档提高精度法的收敛性对比如表1所示。

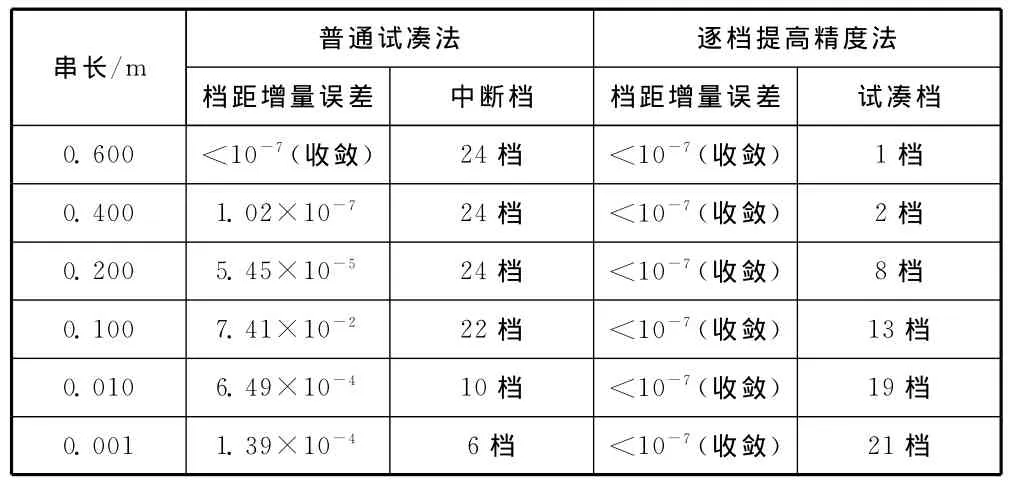
表1 算法收敛性对比

由表1可看出，普通试凑法受迭代精度损失的影响，随地线串长的减少，档距增量误差不断增大，可计算的档数也不断减少，仅通过在第一档试凑，在极端的档距、高差和覆冰组合时难以求出地线的不平衡张力；而对于逐档提高精度的试凑法，当档距增量之和的误差大于阀值时，在前一档试凑求解的基础上提高下一档的精度，可轻松完成任意串长的不平衡张力计算。

3 地线不平衡张力计算

3.1 工程条件

浙北—福州1 000 k V输电线路工程全长2×603 k m，途经浙江和福建历史上发生过多次较严重覆冰断线、倒塔事故的地区，其中15 mm及以上中、重冰区占70%以上，导地线覆冰不平衡张力较大。全线冰区分布如表2所示。

表2 全线冰区分布

该工程15 mm中冰区单回路导地线分别采用8×JL／G1 A－500／45钢芯铝绞线和LBGJ－170－20 AC铝包钢绞线。现以该工程某15 mm中冰区耐张段为例，采用逐档提高精度法进行导地线覆冰不平衡张力及断线张力的验算，耐张段断面如图1所示。

3.2 验算结果

按文献［4］规定，经排列组合验算，导线不均匀覆冰最大不平衡张力出现在前三档覆冰率20%、后三档覆冰率100%时，T4直线塔的不平衡张力最大，验算结果如表3所示；最大断线张力出现在第1档时，T2直线塔的断线张力最大，验算结果如表4所示。

由表3和表4可以看出，地线覆冰不平衡张力和断线张力系数一般大于导线；由于地线断线张力系数通常不会超过规程的规定值100%，故一般不需再进行直线塔地线断线的张力验算；对于覆冰不平衡张力系数，由表3还可以看出，当导线在规程的规定值15%范围内时，地线却超出规程的规定值25%，故

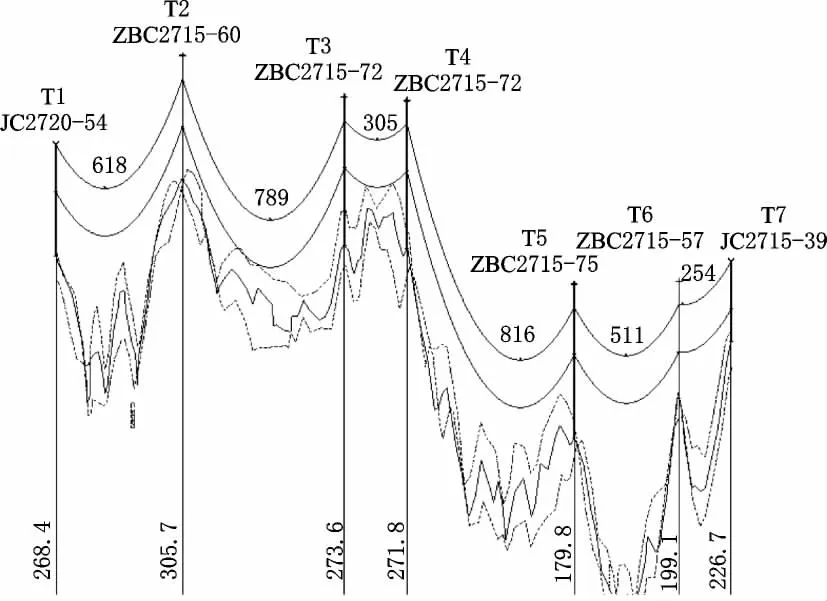
图1 连续档断面图

表3 导地线覆冰不平衡张力

表4 导地线断线张力

对特高压线路覆冰不平衡张力问题，仅进行导线验算而忽视对地线的验算是不科学的。

4 结论

（1）逐档提高精度的不平衡张力计算法具有良好的收敛性，可计算档距多、串长短的地线不平衡张力，应力计算精度可达，并便于软件实现；（2）由于地线断线张力系数通常不会超过规程的规定值100%，故一般不需再进行地线断线张力验算；（3）当导线覆冰不平衡张力系数在规程规定值范围内时，地线也可能超出规程规定值，故有必要加强地线覆冰不平衡张力的验算。

［1］程思勇，薛志方.覆冰不平衡张力计算分析［J］.电网与清洁能源，2011，27（2）：10～13

［2］吕健双，李健.特高压输电线路覆冰断线张力计算与分析［J］.电力科学与工程，2013，29（8）：10～15

［3］廖宗高，陈海波，肖立群，等.特高压输电线路直线塔纵向不平衡张力取值的探讨［J］.电力建设，2006，27（2）：1～3，17

［4］DL／T5440—2009 重覆冰架空输电线路设计技术规程［S］

［5］薛志方，程思勇.置信域算法在输电线路覆冰不平衡张力计算中的应用及不平衡张力的影响因素［J］.电网技术，2012，36（4）：225～228

［6］邵天晓.架空送电线路的电线力学计算［M］.第2版.北京：中国电力出版社，2003