我国粮食产量的波动与预测方法选择

叶 浩，庄大昌，张慧霞

（1.广东财经大学 地理与旅游学院，广东 广州 510320；2.广东财经大学 公共管理学院，广东 广州 510320）

粮食安全一直是全球关注的热点问题，美国世界观察研究所所长Lester R.Brown两次抛出“中国粮食威胁论”，其焦点就是中国的粮食安全问题［1］。当前，中国正处于全面建设小康社会和国家工业化、城镇化加速发展的关键时期，在即将到来的人口增长、工业化、城镇化的三大高峰的客观背景下，粮食问题对国家经济社会发展的制约作用已经开始凸显，并成为政府和学者共同关注的热点［2－4］。中国是一个粮食需求大国，立足于水土资源、经济社会状况和世界粮食安全宏观背景，保障粮食的数量安全仍然是我国未来较长时期需要解决的首要问题。粮食安全直接关系到社会的稳定和国家的安全，为满足经济社会发展的需求，中国的粮食安全仍面临着巨大的挑战。

随着我国农村家庭土地承包经营制度的推行，经过几十年的农业发展与改革，我国粮食供给基本实现了总量基本平衡、丰年有余的历史性转变。但自20世纪80年代中期发生“卖粮难”以来，我国粮食供求陷入了“短缺”与“过剩”的循环波动之中，当粮食生产的增长率达到某一相对较高水平以后，受某些因素的影响，又会下降到一个相对较低水平，甚至连续几年在这个水平上徘徊。粮食产量波动及其预测也因此成为政府和公众关心的焦点问题之一，未来我国粮食产量将如何变动，能否达到国家粮食安全的目标就成为一个很有意义的话题。从当前对粮食产量的预测模型和方法来看，基于灰色理论、ARMA、马尔可夫链与经验模态法（EMD）的时间 序列 模型［5－7］以及综合运 用 以 上 方 法 的 组 合 预 测 模 型［8－11］应用最为广泛，线性回归或双对数模型的回归预测模型［12－13］、基于生物学原理的人工神经网络模型［14］与灾害周期理论［15］等也被用于粮食产量预测之中。但由于中国粮食产量受耕地非农化、作物种植结构、粮食补贴政策、农业生产资料价格上涨、粮价波动及异常气象灾害频繁发生等因素的影响，使得粮食产量预测的准确性受到了极大挑战。如果预测方法选择不当，不仅不会对确保中国粮食安全宏观调控政策产生正面影响，甚至可能还会产生负面影响，更谈不上如何规避决策风险和发挥预警功能。

1 我国粮食产量的波动特征

当前，有关粮食产量预测研究中使用较多的是传统的统计预测技术，如定性与推断技术、时间序列统计模型和回归分析方法。随着计算技术的发展，灰色系统理论、经验模态法（EMD）及人工神经网络预测等新技术也得到广泛应用，构建了许多很有价值的理论假说和预测模型。然而，由于粮食生产是由诸多因素综合影响的不确定系统，使得上述模型的应用受到诸多限制，如果预测方法选择不当，有时甚至出现结论与实际情况完全相反的情况。为了描述中国粮食产量变化的特征，本文利用了对数化后的1952—2012年中国粮食总产量的数据，使用EMD方法提取其趋势项，绘制了粮食产量实际值与趋势值变化曲线图（图1）。

图1 我国粮食产量的增长趋势及其波动Fig.1 Increase trend and fluctuation of grain output in China

从图1来看，自1952年以来，我国粮食产量不断增长，但是存在着明显的波动的特征，而且波幅较大。整体来看，累计30年的粮食产量位于趋势线以上，累计31年的粮食产量位于趋势线以下，正负基本相当。其中粮食产量最长波谷出现在1959—1965年，连续7年在趋势线以下，最长波峰出现在2006—2012年，持续时间为7年。通常一个较长的波峰紧接着就会伴随着一个较长的波谷，如1955—1958年为波峰，1959—1965为波谷；1995—1999为波峰，接下来的2000—2004年为波谷，2005—2012年又变成波峰。从图1中还可以看出我国粮食产量的趋势序列在1952—1976年间的增长曲线是凹函数形式，1977—2012年间为凸函数形式。特别是自1996年之后斜率逐渐降低趋于0，增长陷入停滞状态。相对来说，1996年以来我国粮食产量波动的周期明显变长，波幅变大，说明我国粮食产量波动频率减慢，但是变化的幅度却在增加。

通过观察，我们可以认为我国粮食产量的波动具有周期性的规律，但这并不是我们一般所说的周期，粮食产量表现出的这种周期性波动并没有精确的周期长度，不同波的相位和振幅经常发生偏移，这表明粮食生产是受到非确定性因素影响的非线性系统。通常对这种曲折、非光滑（不可微分）的曲线，用经典数学处理会非常困难，这可能就是上述模型精度普遍不理想的原因所在。分形理论的研究对象是自然界和社会经济领域看起来是无序的、不规则的复杂现象，旨在揭示隐藏在复杂、不规则和混沌的自然或社会现象内部的规律。利用分形理论来研究无序时间序列的演变规律，关键是找出变量序列随着时间变化而呈现出的某种程度上的自相关性。重标极差法（rescaled range analysis，R／S）是刻画这种规律性的有效方法，利用R／S分析模型来对粮食产量演化趋势进行分析具有重要的理论与实践价值。

2 研究方法

1951年英国水文学家Hurst提出了一个非常稳健的无参数统计方法，他发现尼罗河流域的干旱情况并非传统水文统计所设想的那样是一种随机现象，而是干旱越持久，就越可能持续干旱，该现象被 Mandelbrot等在理论上进行了证明，并加以补充和完善，将之称为 Hurst现象［16］。R／S分析也因此成为一种普遍应用于自然及社会经济现象时间序列研究的非线性科学数量分析预测方法，通过这种方法可以区分具有长期非函数周期时间序列与随机序列，其计算原理如下：

假设有一原始时间序Yi，长度为M。首先对原始数据进行处理，逐一计算该序列的自然对数比，用于消除或降低线性依赖程度。这样就可以产生一个新的时间序列Xi，其长度为T＝M－1。以长度n（n≥3）把这个序列均分为A（取T／n的整数部分）个相邻的子区间，每个子序列记为Ra，子序列Ra的元素、均值及标准差分别记为Rk，a、¯Ra和Sa（k＝1，2，…，n；a＝1，2，…，A），则称

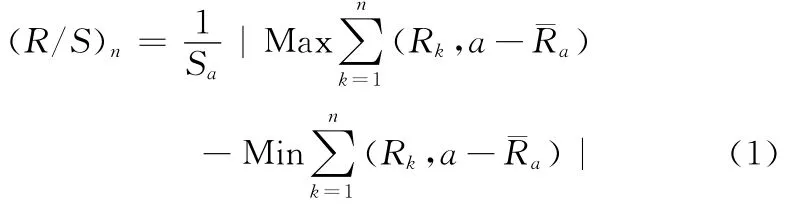
为时间序列Xi在时间增量长度为n上的重标极差（rescaled range）。Hurst通过大量研究发现存在常数H，使得以下公式成立：

式（2）中H称为Hurst指数。在对原始序列进行分割时，根据n的不同取值得到相应的（R／S）n。以Ln（n）为解释变量，Ln（R／S）为被解释变量，通过最小二乘法对Ln（R／S）＝Ln（c）＋H·Ln（n）＋ε进行线性回归，计算得到的方程中的斜率就是Hurst指数的估计值。

时间序列的Hurst指数H居于0～1之间。以0.5为间隔，时间序列在不同的区间会表现出不同的特性：H∈（0，0.5）时，意味着过去的增量与未来的增量呈现负相关，即未来的趋势和过去的趋势正好相反，H值越接近0，这种负相关性或反持续性就越强；H＝0.5时，序列为随机游走，时间序列过去与未来无相关性或只有短程相关；H∈（0.5，1）时，时间序列有自相关性，其增量会表现出长期增长的特性，表明时间序列各变量之间具有长期正相关特征，即未来的趋势往往和过去的趋势正好相同，H值越接近1，这种正相关性或持续性就越强；H＝1时，属于完全预测范围。

3 我国粮食产量波动的R／S分析

按照上述方法，利用分形理论中的R／S方法探讨我国粮食产量的波动趋势是否存在Hurst现象，进而检验粮食产量时间序列的分形现象是呈现持续性、反持续性还是随机性。同时由于中国各个地区的自然资源禀赋，社会经济发展水平及粮食生产方式存在较大的差别，各省区的粮食生产情况必然会存在着较大的差异。为了消除直辖市与其他省级行政区在地域范围等方面的悬殊差别，本文把北京、天津、上海、重庆分别并入紧邻的河北、江苏与四川省进行考察，台湾省、香港和澳门特别行政区的统计数据缺失，未列入研究范围。样本数据主要来自历年《中国农业统计年鉴》，部分数据来自各省区统计年鉴。然后对计算得到的Ln（R／S）－Ln（n）进行回归分析，详细结果见表1。

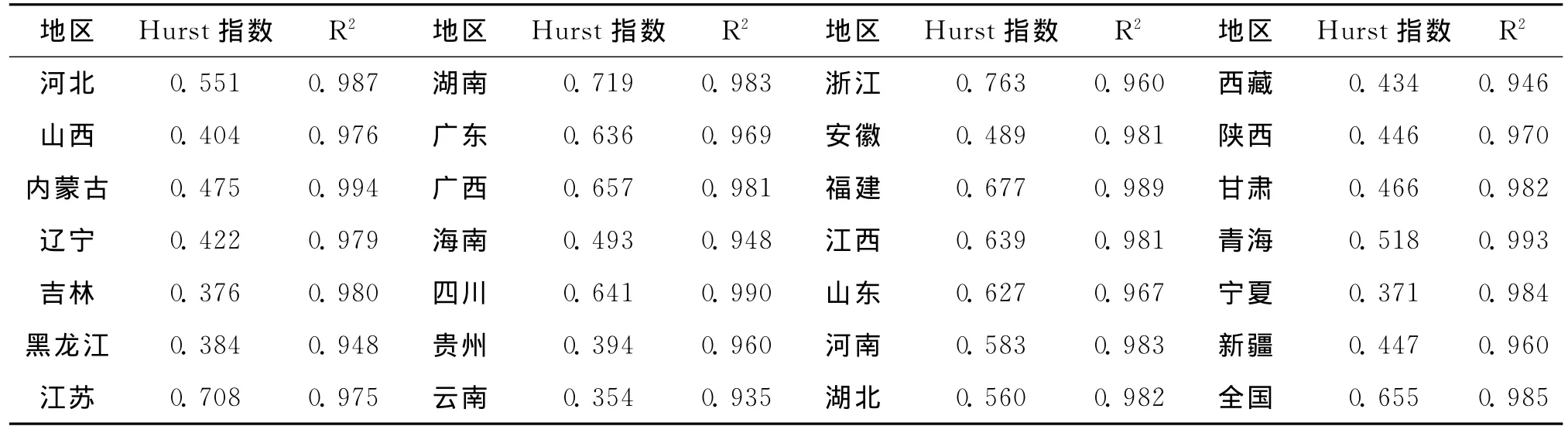
表1 分地区粮食产量的Hurst指数Table 1 Calculated Hurst exponent for grain output at provincial level

整体来看，表1中各省区及全国的回归拟合度R2最低为云南省的0.935，最高为内蒙古的0.994，且均通过了水平为5%的显著性检验，说明应用R／S分析方法对我国粮食产量的波动研究具有较高的精度。在1952—2012年期间，全国粮食产量的Hurst指数为0.655，它大于随机游走假设的临界值0.5，存在着较强的状态持续性，说明我国粮食产量存在较为明显的持久性和分形结构。也就是说如果序列在前一个期间是增（减）的，那么它在下一个期间往往会继续保持增（减）的趋势。但这种持续性影响并不是永久性的，通常经过一段时期之后即会消失。值得注意的是，从1952—2012年期间全国粮食产量波动的特征来看，其在趋势线上下浮动的最长持续时间为7年，也就是说2006—2012年已经连续7年在趋势线以上，因此2013年极有可能是下一个粮食减产阶段的开始。

从表1还可以看出，各个省区的Hurst指数存在较大的差别。其中Hurst指数在0.55以上的省区有河北、江苏、浙江、福建、江西、山东、河南、湖北、湖南、广东、广西与四川，共计12个。在0.45～0.55之间的省份有内蒙古、安徽、海南、甘肃与青海，共计5个。在0.45以下的省份有山西、辽宁、吉林、黑龙江、贵州、云南、西藏、陕西、宁夏及新疆，共计10个。从区域分布来看，Hurst指数较高的省区主要为我国各粮食主产区，其水土资源及气候条件均相对较为优越，粮食生产较少受到偶然因素的影响。Hurst指数相对较低的省区多数水土资源及气候条件相对较差，容易受到气象灾害及其他因素的影响，粮食产量波动相对无序。但安徽与东北3省作为我国的粮食主产区，其Hurst指数却相对较低，这可能和其所处的地理位置有关。东北3省由于纬度较高，容易受到霜冻等低温灾害的影响，而安徽由于地处长江和淮河两大河流的中下游，历来是洪涝灾害的多发地区，因此这4个省区粮食产量的波动较大。

为了更细致的考察各省区粮食产量的波动特征，我们选取了Hurst指数最高的浙江与湖南、Hurst指数距离0.5最近的海南与安徽以及Hurst指数最小的云南与宁夏共计6个代表性省区，绘制了其去除趋势项之后的粮食产量波动的时间序列图（见图2）。

图2 代表性省区粮食产量的波动特征Fig.2 Fluctuation characteristics of the representative province’s grain output

从图2中6个代表性省区粮食产量波动特征可以发现，Hurst指数最高的浙江与湖南粮食产量波动的规律性非常强，其增（减）趋势会维持相当长的一段时期，使用ARMA系列模型进行预测比较合适。而海南与安徽的粮食产量波动基本处于无序的随机状态，使用马尔科夫链模型进行短期预测精度会相对较高。Hurst指数最低的云南与宁夏是反持久性的或遍历性的时间序列，如果其粮食产量在前一时期是增加的，那么他在下一个期间多半是减少的，这种反持久性行为的强度依赖于Hurst指数距离0有多近。这种时间序列比类似海南和安徽的随机序列具有更强的突变性，也称之为均值回复过程，适合使用EMD方法提取趋势线并进行预测。

4 结 论

本文总结了已有粮食产量预测方法与模型的不足，在对我国粮食产量的波动特征进行分析的基础上，运用R／S分形理论对我国及各省区1952—2012年期间粮食产量的波动规律及可预测性进行了研究，结果表明：

（1）自1952年以来，我国粮食产量不断增长，但是存在着明显的波动的特征，往往一个较长的波峰紧接着伴随着一个较长的波谷，正负波动基本相当。全国的粮食产量的趋势序列在1952—1976年间的增长曲线是凹函数形式，1977—2012年间为凸函数形式，增速变缓。自1996年以来我国粮食产量波动的周期明显变长，波幅变大，说明我国粮食产量波动频率减慢，但是变化的幅度却在增加。通过观察，我们可以认为我国粮食产量的波动具有周期性的规律，但这种周期性波动并没有精确的周期长度，波的相位和振幅经常发生偏移。

（2）全国粮食产量的 Hurst指数为0.655，说明在1952—2012年期间，我国粮食产量的时间序列具有较强的持续性，也就是说如果序列在前一个期间是向增（减）的，那么它在下一个期间仍会继续保持增（减）的趋势。但这种持续性影响并不是永久性的，经过一段时期之后将会消失，从而形成一个个循环。不过这些循环没有固定的周期，依靠过去的数据预测未来的变化会存在较大的误差。通过分析我们认为，2013年极有可能是下一个全国粮食减产阶段的开始。

（3）各个省区的 Hurst指数存在较大的差别。从区域分布来看，Hurst指数较高的省区主要为我国各粮食主产区，其水土资源及气候条件均相对较为优越，粮食生产较少受到偶然因素的影响。Hurst指数相对较低的省区多数水土资源及气候条件相对较差，容易受到气象灾害及其他因素的影响，粮食产量波动相对无序。

（4）Hurst指数高的省区粮食产量波动的规律性非常强，其增（减）趋势会维持相当长的一段时期，使用ARMA模型对其短期预测精度会相对较高。Hurst指数在0.5附近的省区粮食产量波动基本处于无序的随机状态，适合使用马尔科夫链模型进行短期预测。Hurst指数低的省区是反持久性的或遍历性的时间序列，这种时间序列比随机序列具有更强的突变性或易变性，也称之为均值回复过程，适合使用趋势线方法进行预测。

［1］Lest R Brown，Brain Halweil.China’s water shortage could shake world food security ［J］.World Watch，1998，11（4）：75－89.

［2］刘彦随，吴传钧.中国水土资源态势与可持续食物安全［J］.自然资源学报，2002，17（3）：270－275.

［3］刘玉杰，杨艳昭，封志明.中国粮食生产的区域格局变化及其可能影响［J］.资源科学，2007，29（2）：8－14.

［4］周力，周应恒.粮食安全：气候变化与粮食产地转移［J］.中国人口·资源与环境，2011，21（7）：162－168.

［5］孙东升，梁仕莹.我国粮食产量预测的时间序列模型与应用研究［J］.农业技术经济，2010（3）：97－106.

［6］毕守东.我国粮食产量的系统预测与控制分析［J］.数量经济技术研究，2000（6）：20－22.

［7］刘会玉，林振山，张明阳.基于EMD的我国粮食产量波动及其成因多尺度分析［J］.自然资源学报，2005，20（5）：745－751.

［8］张峭.中国粮食产量短期（波动）预测［J］.农业技术经济，1998（6）：32－35.

［9］陈永福，吴蓓蓓，王晶晶.基于多变量经验概率模型的中国粮食产量模拟预测分析［J］.系统工程理论与实践，2012，32（11）：2363－2371.

［10］王启平.BP神经网络在我国粮食产量预测中的应用［J］.预测，2002，21（3）：79－80.

［11］姚作芳，刘兴土，杨飞.马尔科夫方法修正的灰色模型在吉林省粮食产量预测中的应用［J］.地理科学，2010，30（3）：452－457.

［12］吕学梅，宋莹华，郭立运.趋势－ARMA组合模型在山东粮食产量预测中的应用［J］.中国人口·资源与环境，2011（S2）：193－195.

［13］王波，郭夜白，高来斌，等.最优加权预测在吉林省粮食产量预测中的应用［J］.吉林农业大学学报，2008，30（5）：760－763.

［14］李宝仁，邬琼 ，刘寅.最优加权组合法在中国粮食产量预测中的应用研究［J］.统计与决策，2010（19）：34－38.

［15］周季华，杨言勇.1994年及未来我国粮食产量的预测与分析［J］.统计与决策，1994（6）：26－28.

［16］Mandelbrot B B，Wallis J R.Some long－run properties of geographical records［J］.Water Resource Research，1969，5（1）：321－340.