向量中立型抛物Robin边值问题的振动性分析
罗李平
(衡阳师范学院 数学与计算科学系,湖南 衡阳 421002)
0 引 言
1970年,Domslak[1]在研究向量微分方程时首次引入了H-振动性的概念,其中H是一个单位向量。H-振动性的概念是研究向量微分方程的新的有力工具。关于这一概念及其应用,1996年Courant和Hilbert在文[2]中作了很好的阐述。最近,一些学者把H-振动性的概念运用于(脉冲)向量偏微分方程的H-振动性研究上,也取得了一些很好的研究成果[3-10]。本文将考虑如下的一类向量中立型抛物边值问题。
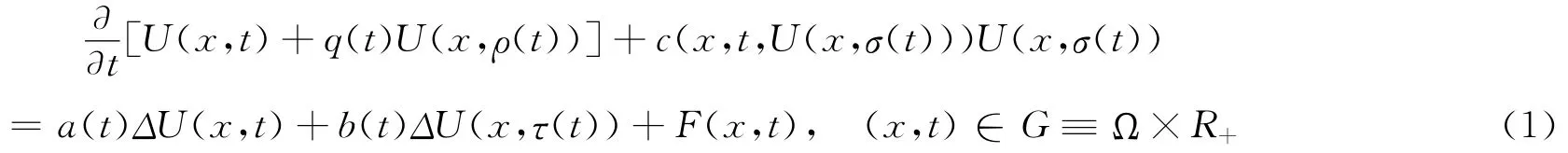
解的H-振动性问题,其中U(x,t)∈C2(Ω×[t0,∞),Rm)是向量函数,Ω是Rn中具有逐片光滑边界的有界域,Δ是Rn中的n维Laplacian算子,R+=[0,∞)。同时考虑Robin边值条件:
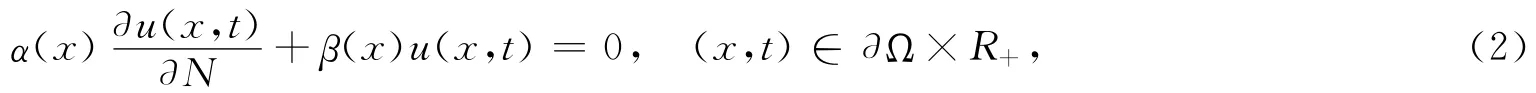
其中0是Rm中的零向量,N 是∂Ω的单位外法向量,α(x),β(x)∈C(∂Ω,(0,∞)).
在本文中,我们总假设下列条件成立:
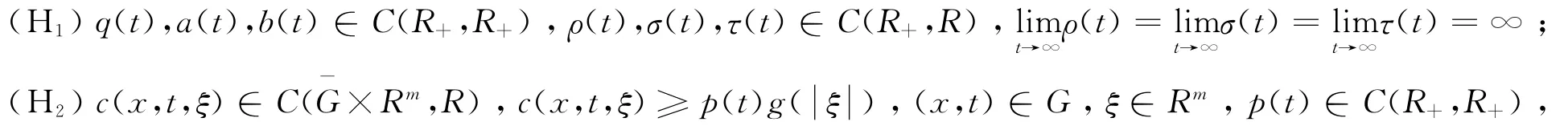

定义1 向量函数U(x,t)∈C2(Ω×[t0,∞),Rm)称为边值问题(1),(2)的解,若U(x,t)在G上满足方程(1)及在∂Ω×R+上满足边界条件(2)。
定义2 边值问题(1),(2)的解U(x,t)称为在G内H-振动,若对Rm中的单位向量H 及任意大的T≥0,存在一点 (x0,t0)∈ Ω×[T,∞),使得内积 <U(x0,t0),H >=0。
1 主要结果及其证明
为了讨论边值问题(1),(2)的H-振动性,我们在Ω上考虑Robin特征值问题:

令λ0是问题(3)的第一特征值,则据文献[11]知,λ0>0,且∀x∈Ω,其相应的特征函数φ(x)>0。
为叙述方便,在本文中引入如下记号:
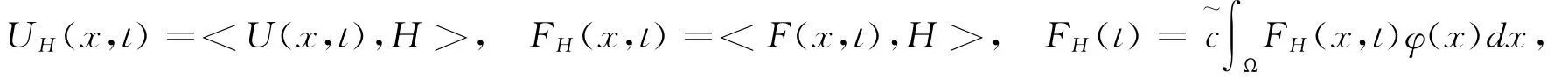

定理1 设(H1)-(H2)成立,U(x,t)是方程(1)的解。若UH(x,t)最终为正,则UH(x,t)满足纯量双曲型偏微分不等式
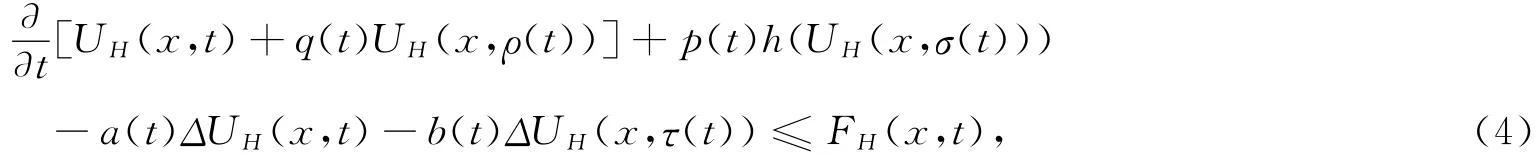
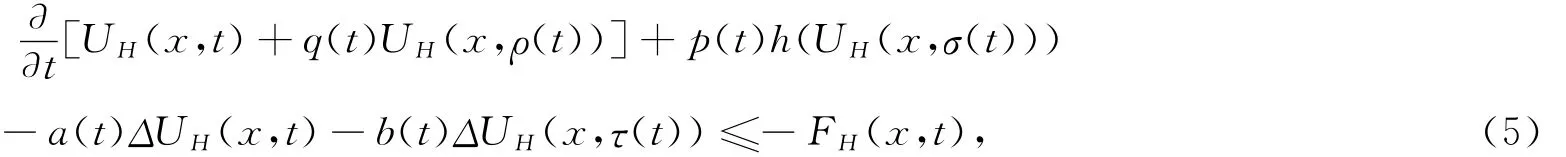
证明 设UH(x,t)最终为正。将方程(1)两边与H作内积,由内积性质可得
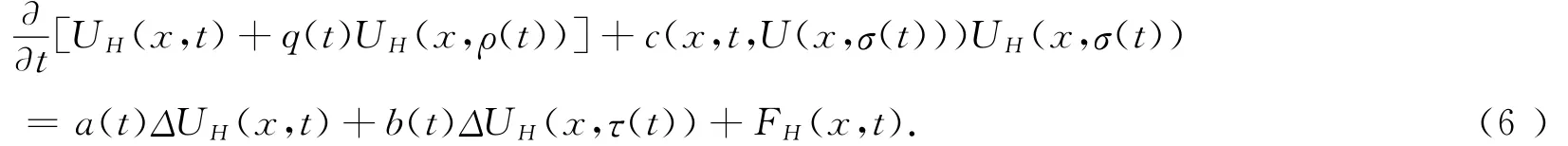
注意到(H2),我们有
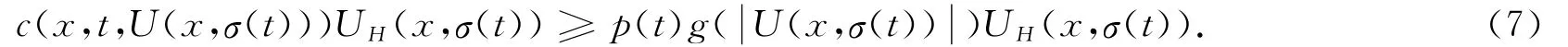
利用Schwarz不等式,我们可得

注意到g(ξ)非减,由(7)-(8),我们有
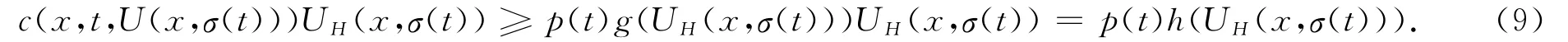
于是联合(6)和(9),即得(4),亦即UH(x,t)满足(4)。
若UH(x,t)最终为负,易知
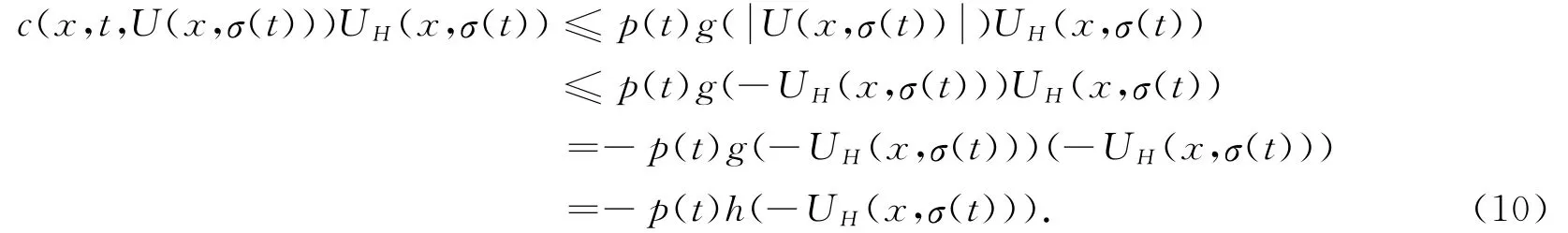
用-1乘(6),利用(10)可知VH(x,t)=-UH(x,t)满足(5)。证毕。
相应于边值条件(2),考虑纯量边值条件:
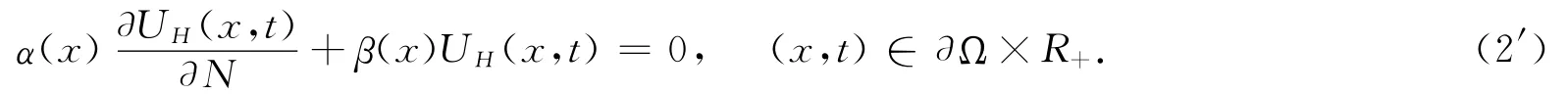
定理2 设(H1)-(H2)成立。若纯量双曲型偏微分不等式

在边值条件 (2′)下无最终正解,则边值问题(1),(2)的任意解U(x,t)在G内H-振动。
证明 设边值问题(1),(2)在G内存在非 H-振动解U(x,t)。若UH(x,t)最终为正,则由定理1可知,UH(x,t)满足 (11)+,且易知UH(x,t)满足边值条件 (2′),此与题设矛盾。若UH(x,t)最终为负,则VH(x,t)=-UH(x,t)是满足 (11)- 和边值条件 (2′)的最终正解,同样与题设矛盾。证毕。
定理3 设(H1)-(H3)成立,其中
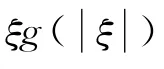
若泛函微分不等式
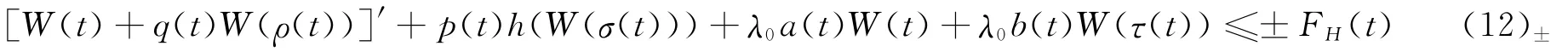
无最终正解,则边值问题(1),(2)的任意解U(x,t)在G内 H-振动,其中λ0由问题(3)确定。
证明 设边值问题(1),(2)在G内存在非 H-振动解U(x,t)。若UH(x,t)最终为正,(x,t)∈Ω×[T,∞),T≥0,我们用c~φ(x)乘(4),并在区域Ω上关于x积分,得
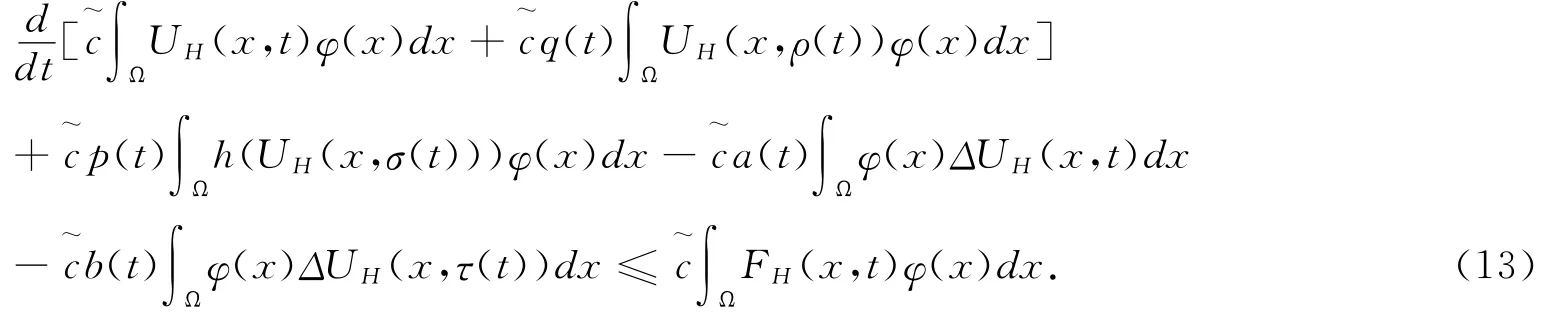
由Green公式及边界条件(2′),我们有
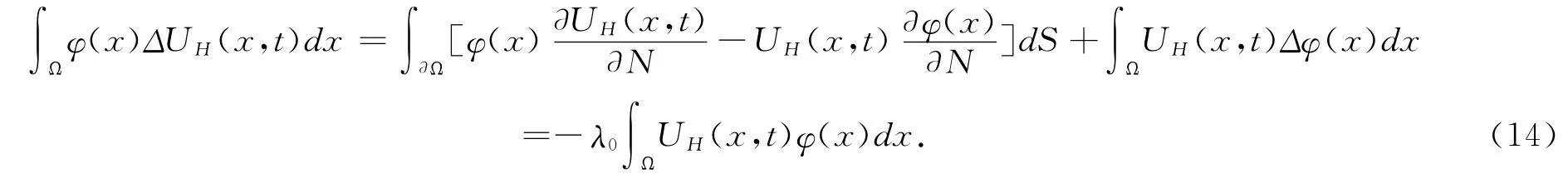
类似地有

利用Jensen不等式,我们有
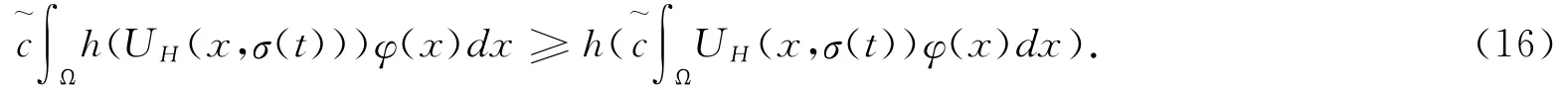

此示W(t)是不等式(12)+的一个最终正解,而这与定理2的题设矛盾。
若UH(x,t)最终为负,(x,t)∈Ω×[T,∞),T≥0,令VH(x,t)=-UH(x,t),类似于上面的过程,结合(12)-,同样可以得到矛盾。证毕。
定理4 设(H1)-(H3)成立。若对充分大的T,有

则边值问题(1),(2)的任意解U(x,t)在G内 H-振动。
证明 设边值问题(1),(2)在G内存在非 H-振动解U(x,t)。若UH(x,t)最终为正,(x,t)∈Ω×[T,∞),T≥0,则由定理3的证明可知,微分不等式


在区间 [T,t]上对(19)积分,可得


若UH(x,t)最终为负,(x,t)∈Ω×[T,∞),T≥0,令VH(x,t)=-UH(x,t),类似于上面的过程,结合条件(18),同样可以得到矛盾。证毕。
[1]Domslak Ju I.On the oscillation of solutions of vector differential equations[J].Soviet Math.Dokl.,1970,11:839-841.
[2]Courant R,Hilbert D.Methods of Mathematical Physics,Vol.I[M].New York:Interscience,1996.
[3]Minchev E,Yoshida N.Oscillation of solutions of vector differential equations of parabolic type with functional arguments[J].J.Comput.Appl.Math.,2003,151(1):107-117.
[4]Li W N,Han M A,Meng F W.H-oscillation of solutions of certain vector hyperbolic differential equations with deviating arguments[J].Appl.Math.Comput.,2004,158(3):637-653.
[5]罗李平.具连续分布滞量的中立型向量抛物偏泛函微分方程的 H-振动性[J].数学的实践与认识,2008,38(11):158-162.
[6]罗李平,杨柳.具连续偏差变元的中立型向量抛物偏微分方程的 H-振动性[J].纯粹数学与应用数学,2009,25(4):801-806.
[7]Li W N,Han M A.Oscillation of solutions for certain impulsive vector parabolic differential equations with delays[J].J.Math.Anal.Appl.,2007,326(1):363-371.
[8]罗李平,俞元洪.脉冲向量中立型抛物偏微分方程的 H-振动性[J].数学学报,2010,53(2):257-262.
[9]罗李平,王艳群,宫兆刚.具脉冲和时滞影响的向量抛物型方程振动性的新准则[J].中山大学学报:自然科学版,2012,51(2):45-48.
[10]罗李平,王艳群,谢作政,等.带脉冲和时滞效应的向量抛物Dirichlet边值问题的振动判据[J].生物数学学报,2013,28(3):423-427.
[11]叶其孝,李正元.反应扩散方程引论[M].北京:科学出版社,1990:135.

