基于频率约束的拓扑优化中局部模态现象的数值模拟分析*
赵志军
(长沙大学土木建筑工程系,湖南长沙 410022)
基于频率约束的拓扑优化中局部模态现象的数值模拟分析*
赵志军
(长沙大学土木建筑工程系,湖南长沙 410022)
针对频率约束下重量最轻的结构拓扑优化问题,通过数值模拟分析,找到能有效避免局部模态的有理分式材料模型,建立了一种合理的结构刚度与质量的关系,所给出算例表明,该模型能有效避免局部模态的发生.
拓扑优化;频率约束;局部模态
随着工程结构日益轻量化和复杂化,对结构设计理论提出了新的挑战.结构拓扑优化方法为结构概念设计提供了更为有效的设计手段.自结构拓扑优化设计概念被提出以来[1],相继出现了变厚度法、均匀化方法、变密度方法[2]和结构渐进优化法(简称ESO法)[3]等方法.
为满足工程中结构对动力特性的要求,结构动力优化设计是一项更具有意义的课题.使用拓扑优化技术进行结构自然频率最大化设计时,低拓扑变量区域结构密度与刚度的差异较大可能导致局部模态现象出现[4,5].由于局部模态频率比结构的整体模态频率小得多,对于频率约束下重量最轻的结构拓扑优化问题,拓扑变量比较低的区域内出现局部模态会导致所追踪的频率为局部模态频率,而非真实的结构频率,从而导致拓扑优化求解失败[6].本文针对于仅频率约束下重量最小的连续体结构拓扑优化问题,基于分式有理式材料插值模型[7],通过分析及数值试验,找到能有效避免局部模态出现的有理分式材料模型,建立了一种合理的结构刚度与质量的关系.所给出算例表明,该模型能有效避免局部模态的发生.
1 单元性质参数的识别
用过滤函数fw(ti)、fk(ti)、fm(ti)识别重量和刚度等性质参数[6],采用如下公式

其中wi,[ki],[mi]分别表示拓扑变量为ti的状态对应的单元重量,单元刚度矩阵和单元质量矩阵;w0i,[ki0],[mi0]分别表示单元固有重量,单元固有刚度矩阵和单元固有质量矩阵.类似于文献[7],这里取

2 变频率区间约束限的结构优化等效模型和求解方法
2.1 变频率区间约束限的结构优化等效模型

为了保证一阶近似式的成立,类似与文献[7],对频率约束采用变区间渐进约束的方式将模型(3)转化为模型(4)进行求解.


2.2 频率显式表示式

2.3 变频率区间约束优化模型处理和求解方法
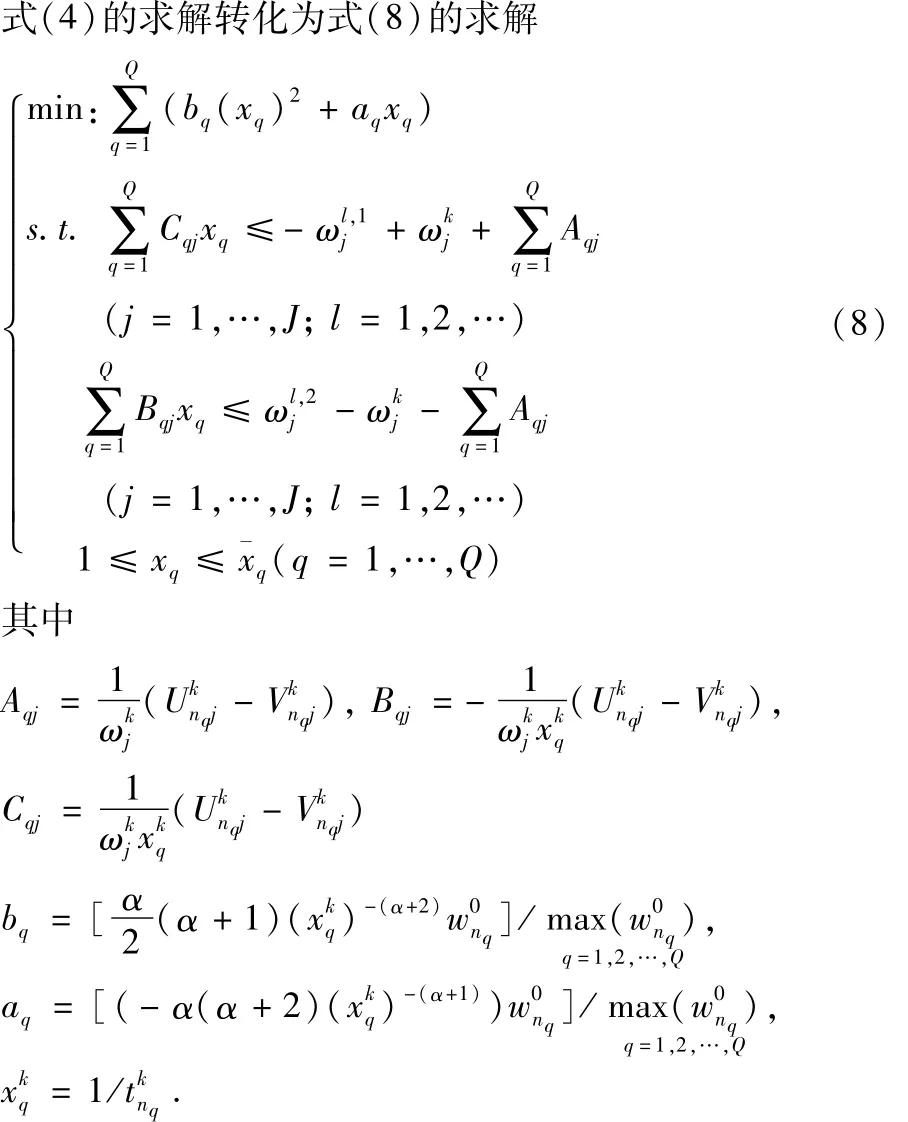
采用类似于文献[7]的方法处理棋盘格问题,再利用对偶理论将模型(8)的规划问题转化为如下的对偶规划问题求解


解此二次规划,求出λ,再由K-T条件求出x*,进而求出t*.这里,为了更好的分析局部模态现象,类似于文献[7],将优化过程分成两个阶段,第一阶段不对结构进行更新,第二阶段采用设计空间调整的策略对结构进行更新.
3 单元刚度与质量比与局部模态的关系
3.1 单元刚度与质量比与各参数的关系


图1 密度函数与刚度函数之比与t的关系

图2 密度函数与刚度函数之比与α的关系
3.2 数值试验与机理分析
如图3所示,梁的尺寸为5m×1m,两端固定约束.材料弹性模量为200GPa,泊松比取为0.3,厚度为0.1m,密度为7800kg/m3.设计区域划分为100×25的有限元网格.设置结构第一阶频率约束为255Hz.这里β1取值为0.02.

图3 梁结构初始设计区域
采用变频率区间约束限的方法求解,首先取v=12.8,α=1.2试算,第一阶段第11个循环迭代步出现局部模态,导致求解失败.该局部模态下的拓扑变量分布和振型如图4所示,其中颜色较深部分拓扑变量接近1,颜色较浅部分拓扑变量值均小于0.1.采用该局部模态下的拓扑变量分布,改变α值进行模态求解计算.在区间α∈(1.0,2.0)中取80个数值进行计算,图5显示不同的α取值下局部模态情况统计,从图中可以看出,α∈(1.0,1.10)时为结构振动没有出现局部模态,在α∈(1.10,1.11)处于过渡阶段,α∈(1.11,2.0)时为结构振动为局部模态.图6显示几种不同的α取值下的振型.上述结果说明α取值在1附近是比较合理的.

图4 α=1.2发生局部模态时拓扑变量分布和振型图
再通过数值试验分析,取α=1,v∈(3.0,19.0)中取80个数值进行模态分析,局部模态情况统计如图7所示.统计数据表明,当v∈(6.0,14.0)区间时,模态分析均为整体振动.

图5 不同的α取值下局部模态情况统计
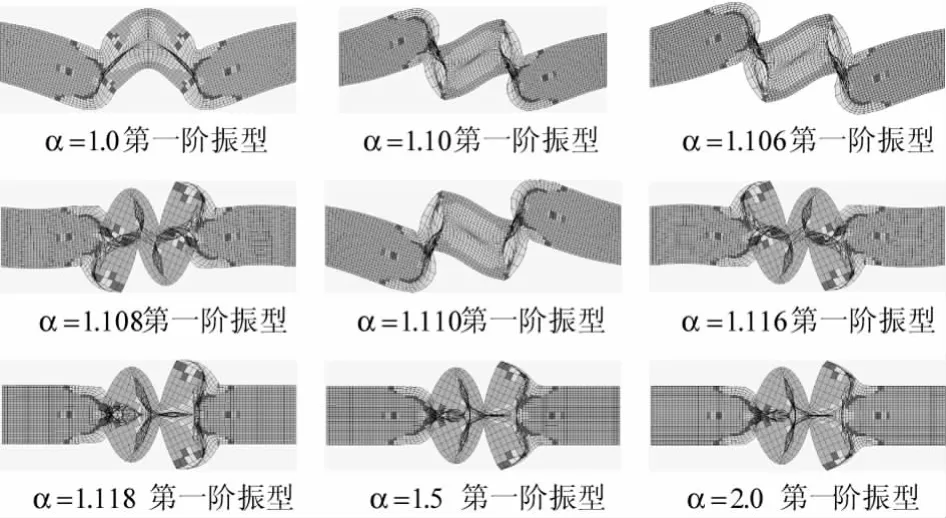
图6 不同的α取值下的振型图

图7 不同的v取值下局部模态情况统计

图8 不同的v取值下的振型图
从上述理论分析和数值试验可以看出,刚度与质量的关系的选取与局部模态的产生是有直接关系的.若能找到一种合理的刚度质量关系,是可以有效避免局部模态的,从而实现结构优化求解.
4 算例
如图3所示梁结构,采用本文方法进行求解.
优化求解第一阶段取v=12.8,α=1.0,计算求解过程中未出现局部模态现象.图9(a~f)显示采用本章方法获得的梁结构拓扑优化历程(图9(f)为最佳结构),共用了29个大循环迭代步.一阶频率从175.2Hz增加到253.7Hz.相应的结构质量的进化历程、频率值变化历程分别见图10和图11.

图9 本文方法得到的梁结构拓扑优化历程
(a)第2轮迭代步,结构重量为3499.82kg,一阶频率为195.5Hz
(b)第7轮迭代步,结构重量为3118.21kg,一阶频率为214.0Hz
(c)第17轮迭代步,结构重量为2725.92kg,一阶频率为236.6Hz
(d)第20轮迭代步,结构重量为2749.28kg,一阶频率为232.7Hz
(e)第24轮迭代步,结构重量为2474.16kg,一阶频率为251.4Hz
(f)第29轮迭代步,结构重量为2424.24kg,一阶频率为253.7Hz

图10 结构质量演化历程

图11 前四阶固有频率演化历程
5 结论
本文针对于频率约束的拓扑优化中局部模态现象,通过数值试验分析,找到能有效避免局部模态的有理分式材料模型.给出的算例结果利用所得到关系能获得有较好0-1分布特征的优化拓扑,具有一定的理论和工程应用价值.
[1]Bendsøe M P,KikuchiN.Generating optimal topologies in structural design using a homogenization method[J].Comput Method,1988,(71):197-224.
[2]石连栓.离散变量结构优化设计算法研究综述[J].天津职业技术师范学院学报,2001,(1):5-9.
[3]Me YM,Steven G P.A simple evolutionary procedure for structural optimization[J].Computers and Structures,1993,(49):885-896.
[4]朱继宏,张卫红,邱克鹏.结构动力学拓扑优化局部模态现象分析[J].航空学报,2005,(4):619-623.
[5]Pedersen N L.Maximization of eigenvalues using topology optimization[J].StructMultidisc Optim,2000,(1):2-11.
[6]隋允康,彭细荣.结构拓扑优化ICM方法的改善[J].力学学报,2005,(2):190-198.
[7]荣见华,张强,葛森,等.基于设计空间调整的结构拓扑优化方法[J].力学学报,2010,(2):256-267.
(作者本人校对)
Numerical Simulation Analysis of Localized M odes
in Structures Topology Optim ization w ith Frequency Constraints
ZHAO Zhijun
(Department of Civil Engineering,Changsha University,Changsha Hunan 410022,China)
One of themain problems in the structural topology optimization with frequency constraints is the appearance of localized modes.In order to avoid localizedmodes,this paper presents a reasonable relationship between the stiffnessmatrix andmassmatrix by introducing the rational approximation material model and using numerical simulation analysis method.One example is provided to demonstrate that the proposed method is feasible and effective for avoiding localized modes.
topology optimization;frequency constraints;localized mode
TU311.3;TB123
A
1008-4681(2014)05-0023-04
2014-09-10
长沙大学科研基金项目(批准号:CDJJ-10010110).
赵志军(1982-),男,辽宁葫芦岛人,长沙大学土木建筑工程系讲师,硕士.研究方向:结构拓扑优化设计.

