多变量耦合系统PID神经网络控制方法研究
朱 林,吴冬雪,赵 倩
ZHU Lin1, WU Dong-xue1, ZHAO Qian2
(1. 内蒙古科技大学 信息工程学院,包头 014010;2. 中海石油海南天然气有限公司,海口 578001)
0 引言
以多变量、强耦合、非线性为特点的复杂工业过程控制,一直是控制理论与控制工程领域的研究热点和前沿。复杂工业过程控制由于数学模型变量多、变量间耦合、非线性和高阶,相应控制器设计困难。
在工业控制中,PID控制一直是通用、有效的控制方法[1]。但是,面对多变量、强耦合、非线性为特点的复杂工业过程,PID控制效果会变差甚至不可控。神经网络具有很强的自学习、自适应和任意非线性表达能力,近年来逐渐应用于复杂系统的控制中。当系统存在不确定性因素时,更能体现神经网络的优越性。文献[2]以二变量耦合时变系统为对象,设计了一种PID神经网络模型。该模型与用神经网络对PID控制器参数进行辅助修改的方法有本质的区别[3,4]。应用PID神经网络控制时,无需为对象的参数和系统结构进行辨识,可根据对象参数变化时对系统输出的影响,“在线”地调整PID神经网络的权值,较好地解决了多变量、耦合系统的控制难题。
但是,PID神经网络中权值采用梯度学习算法,初始权值随机给定,造成网络权值修正较慢且容易陷入局部最优,为了达到满意的训练效果,需要多次的给定,而给定的方法并不能保证每次给定均能达到期望控制效果[5]。为改善上述不足,笔者分析研究了用遗传算法、蚁群算法等方法优选PID神经网络的初始权值的可行性,研究发现,遗传算法对PID神经网络初始权值优化效果较好。本文以三输入、三输出、非线性、耦合系统为控制对象,设计构建了优化初始权值的PID神经网络。同时,为了提高PID神经网络学习效率和预测精度,在网络权值修正算法中加入了动量项。MATLAB仿真结果证明:该方法在提高控制精度,精确解耦方面效果好。
1 多变量非线性强耦合系统
设被控对象具有多变量、非线性、强耦合的性质,共有3个输入,3个输出,系统的传递函数如下:
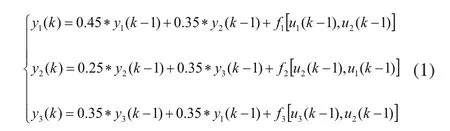
其中非线性函数为:
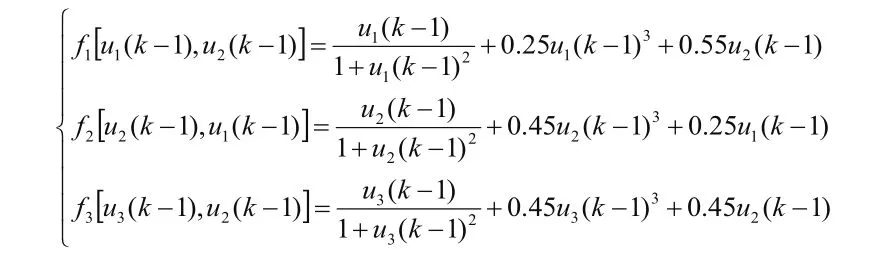
由于该系统的特点,采用传统的PID控制器很难得到理想的控制效果。
2 遗传算法优选初始权值的PID神经网络解耦控制器
根据上述被控对象特点,PID神经网络解耦控制器设计为6×9×3的三层前向网络,即3个并列的子网络。控制系统结构如图1所示。各层的输入、输出函数见文献[6],本文不再赘述。
图1中,xs1、xs2、xs3为系统被控量的给定值;u1、u2、u3为被控对象的输入;y1、y2、y3为被控量当前值;wsij为输入层至隐含层的连接权值;w′sjh为隐含层至输出层的连接权值;其中s为并列子网络的序号,s=1,2,3;i为输入层神经元序号,i=1,2;j为隐含层神经元序号,j=1,2,3;h为输出层神经元序号,h=1。
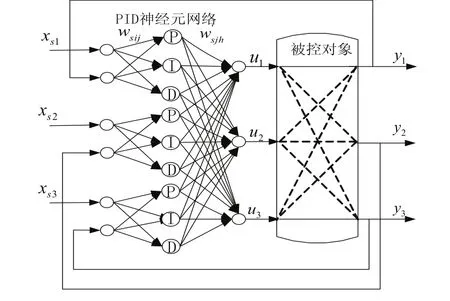
图1 三变量PID神经网络解耦控制系统
2.1 PID神经网络初始权值优选方法
为改善上述提出的PID神经网络不足,采用遗传算法对PID神经网络初始权值进行优选,方法如下:
1)将网络的权值用一组十进制编码的实数表达。任一组完整的权值相当于一条染色体(WR= (wsij,wsjh)=(w1ij,w2ij,w3ij,w1jh,w2jh,w3jh)),本系统中网络的初始权值共有45个。这样的染色体共有R个,即权值种群规模为R。
2)在遗传算法中,适应度函数为进化目标,只能向适应度值增大的方向进化。在选择运算中,适应度值较大的染色体有较大的存在机会。目标函数为在进化代中搜索网络误差最小的染色体。表达式如下:
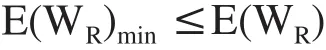
由于网络误差是非零正数,可将目标函数的倒数作为适应度函数。则其适应度函数为:
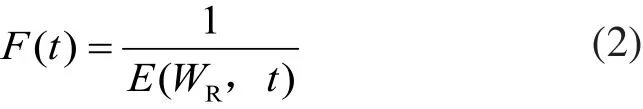
其中,E(WR,t)为第t个进化代染色体WR所具有的目标函数。
3)遗传算法
选择运算中,本研究采用基于适应度比例的选择策略,每个染色体选择概率PR为:
PR=FR/∑FR,其中FR为种群中第R个染色体的适应值。
交叉运算中,本研究采用实数交叉法,设2个染色体为Wkj,Wlj,即第k个染色体和第l个染色体在j位交叉运算后产生的新个体为[7]:

变异运算中,采用非均匀变异操作,选取Wij即第i个染色体的第j个基因进行变异[8],变异操作方法如下:
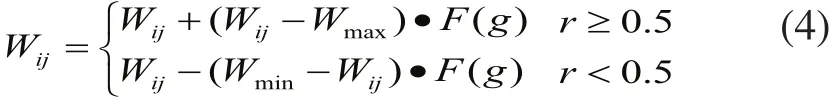
式中:Wmax、Wmin为染色体Wij的上下界;F(g)=r(1-g/Gmax),r为[0,1]间的随机数;g为当前迭代次数;Gmax是最大进化次数。
为了保证算法的收敛性和收敛速度,同时防止出现早熟现象,对遗传算法进行了改进。引入移民,在进化过程中利用种群的标准均方差来衡量群体的早熟程度,一旦发现种群早熟,就按一定的规则产生一定数量的高品质移民来替换种群中的劣质个体[9],早熟判断规则如下:
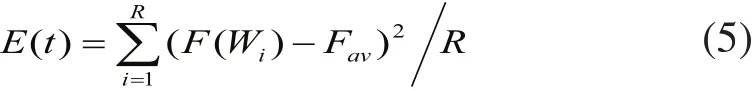
式中:E(t)为第t代种群中的均方差;Wi为种群中第i个染色体;Fav为当前种群中的平均适应度。
通过遗传算法选出最优的一组初始权值,赋值给网络初始权值,然后PID神经网络通过对权值的不断修正,使系统的输出跟随给定值变化。
2.2 PID神经网络权值的修正
在控制的过程中,PID神经网络根据控制量误差按照梯度修正法修正权值,使控制量不断接近控制目标值,权值修正的过程如下。
目标函数:
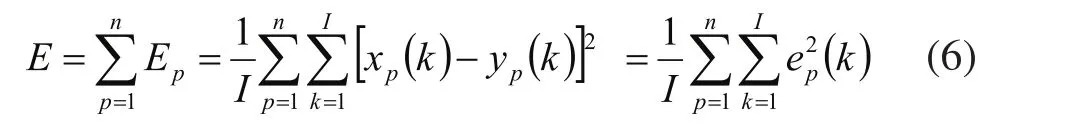
式中:I为每批采样点数,I=100;n为被控变量个数,n=3;xp为期望输出;yp为系统实际输出。
按照梯度下降法调节PID神经网络权值,经k步训练和学习后的权值分别由以下各式确定[10]。
1)隐含层至输出层的权值修正公式:

2)输入层至隐含层的权值修正公式:

式中:xsi为输入层神经元的输入值; v’sj为隐含层神经元的输出值;
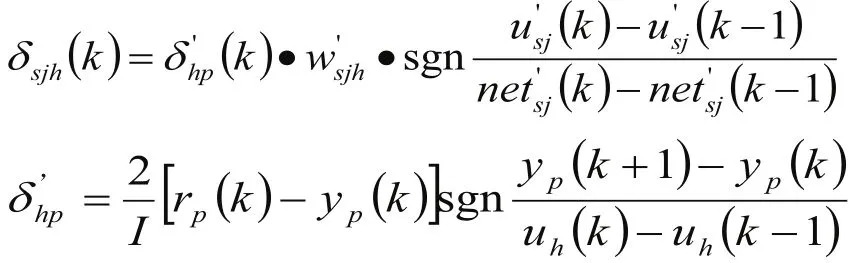
为提高网络学习效率,在式(8)基础上增加了动量项,增加动量项后,隐含层到输出层权值算法和输入层到隐含层权值算法如下:
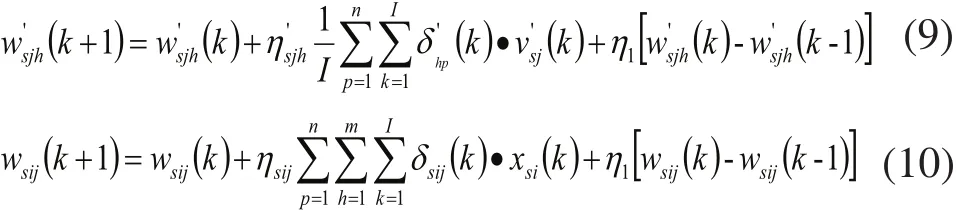
在PID神经网络加入动量项后,可以有效的调节网络的收敛速度,起到缓冲与平滑的作用。
3 仿真研究
为验证上述遗传算法优化后的PID神经网络控制器对复杂耦合系统的解耦控制效果,本文使用Matlab软件对式(1)所示的3输入、3输出多变量、非线性、强耦合系统进行仿真。
3.1 优化PID神经网络初始权值
遗传算法中迭代数最大为截止条件。通过上述优选方法的介绍,遗传算法优化初始权值流程如图2所示。
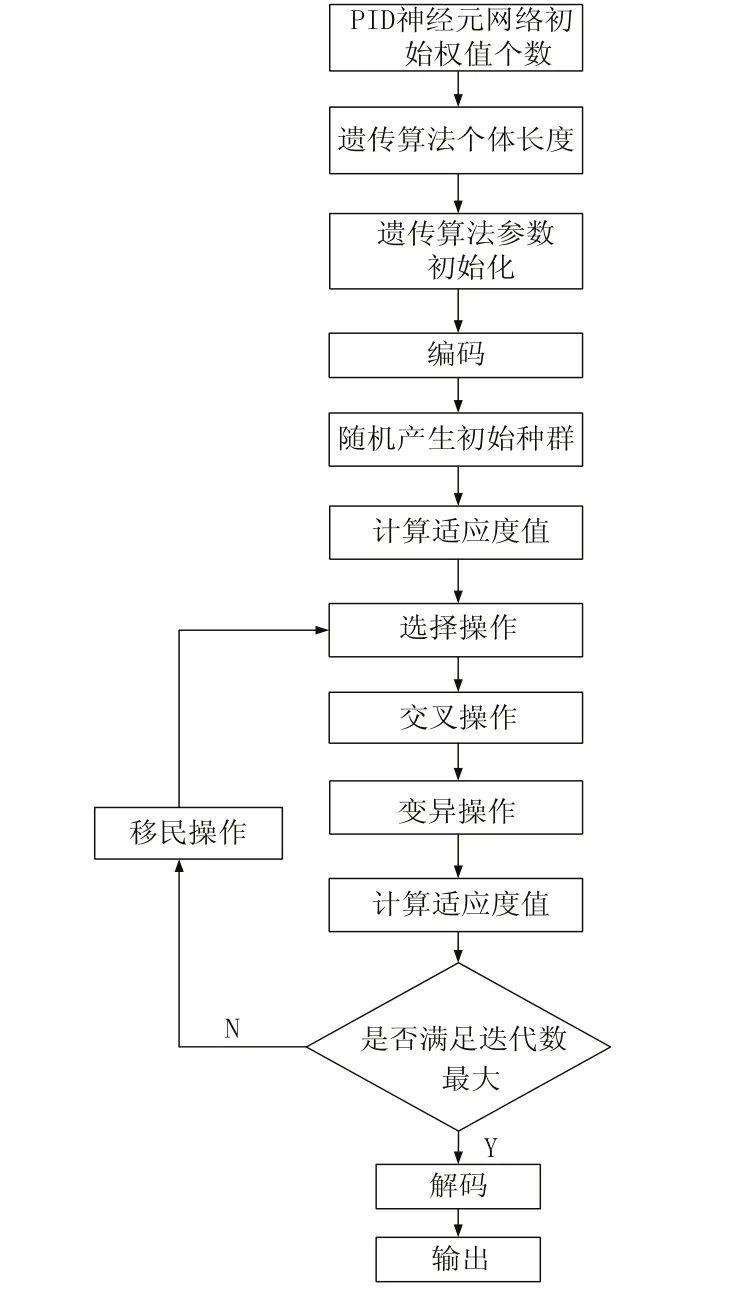
图2 遗传算法优化初始权值流程图
按照流程图编写遗传算法优化初始权值的Matlab程序,通过遗传算法优化后的初始权值为W=[0.0122,-0.0685,1.0469,0.1986, 0.5529,0.1452,…,-2.0976,0.1492,0.2108],把遗传算法优化得到的最优个体W赋值给PID神经元网络初始权值。设置网络权值学习速度为0.005,控制间隔时间为0.001秒,PID神经网络的权值修正采用增加动量项的权值修正算法如式(9)、式(10)。
3.2 PID神经网络控制系统响应效果
系统给定输入X为阶跃信号,即:
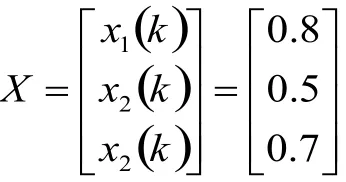
遗传算法优化前后的PID神经网络解耦控制系统对应输出响应如图3和图4所示。
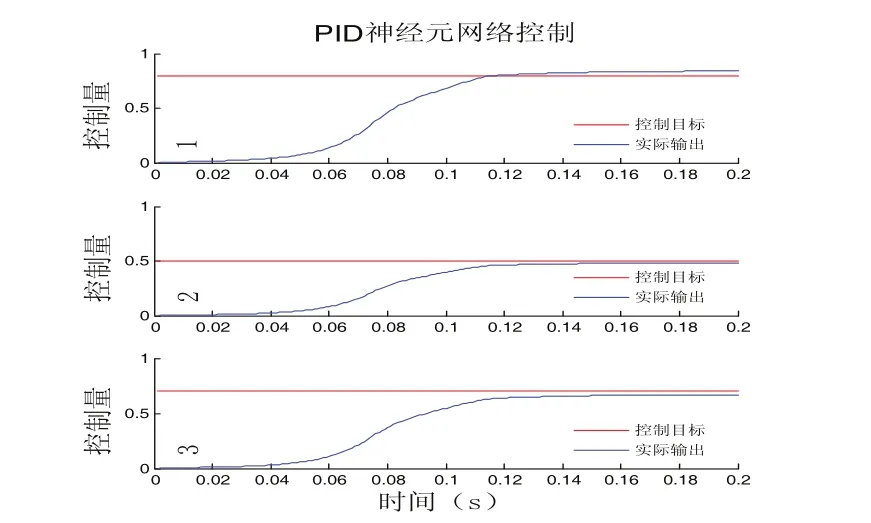
图3 初始权值随机选取的PID神经网络控制器控制效果

图4 遗传算法优化的PID神经网络控制效果
网络目标函数(系统误差均方值)动态曲线如图5和图6所示。

图5 优化前网络目标函数曲线

图6 优化后网络目标函数曲线
响应效果分析:
1)从图3、4可知,优化前后,系统的超调量都非常小。
2)图3中显示,PID神经网络控制器能够控制多输入、多输出复杂耦合系统,系统的实际输出跟随控制目标变化,调节时间为0.12s。
3)图4说明优化后的PID神经网络能够使系统保持较高的稳态精度和较快的响应速度,调节时间为0.02s。
4)分析图5和图6,优化前后网络误差平方均值分别在0.09s、0.025s的时候接近0,说明优化后的PID神经网络系统控制效果更佳,调节时间更短,具有更好的自学习、自适应和解耦能力。
4 结论
1)在工业生产过程中,对复杂耦合系统的控制,传统PID控制难以达到控制要求。文中构建的PID神经元网络基本消除了对象之间的耦合作用。
2)遗传算法优化后的PID神经网络系统响应速度更快,控制精度更高。
3)基于遗传算法的PID神经网络解耦控制,完全可以不依赖于对象模型,通过网络的训练和学习实现多变量、非线性、强耦合系统的解耦。
[1]刘金琨.先进PID控制及其MATLAB仿真 [M].北京:电子工业出版社,2003:1-4.
[2]舒怀林.PID神经元网络对强耦合带时延多变量系统的解耦控制[J].控制理论与应用,1998,15(6):920-924.
[3]廖芳芳,肖建.基于BP神经网络PID参数自整定的研究[J].系统仿真学报,2005,17(7):1711 -1713.
[4]黄剑平.基于BP神经网络的PID控制研究[J].计算机仿真,2010,27(7):167-170.
[5]袁朝辉,张慧.多温区电加热炉的PID神经网络控制[J].计算机仿真,2010,27(12):176-180.
[6]舒怀林,李柱.基于PID神经元多层网络的多变量解耦控制系统[J].自动化仪表.1998,19(3):24-27.
[7]李敏强.遗传算法的基本理论与应用[M].北京:科学出版社.2004.
[8]李敏远,都延丽.基于遗传算法学习的复合神经网络自适应温度控制系统[J].控制理论与应用,2004,21(2):242-246.
[9]欧阳森,王建华.一种新的改进遗传算法及其应用[J].系统仿真学报.2003,15(8):1066-1068.
[10]舒怀林.PID神经元网络及其控制系统[M].北京:国防工业出版社.2006.

