基于蚁群算法的飞机加油车辆调度问题研究

刘长有 LIU Chang-you；王一飞 WANG Yi-fei

（中国民航大学，天津 300300）

（Civil Aviation University of China，Tianjin 300300，China）

0 引言

飞机加油是机场运行的基本内容，安全、有序、高效的完成飞机加油作业是机场运行追求的目标。对飞机加油作业影响最大的是加油车辆的管理与调度。安全有序的车辆管理加上最优化的行驶路线调度是保证按时完成加油作业的关键，因此对飞机加油车辆调度的研究与仿真便成了十分重要的问题。车辆调度是一个VRP（Vehicle Routing Problem）问题，最早由Dantzig和Ramser于1959年提出，是旅行商问题（Traveling Saleman Problem,TSP）的特例，是一个NP难题。Bodin于1983年将车辆优化调度问题分为VRP(Vehicle Routing Problem)问题和VSP(Vehicle Scheduling Problem)问题，后来两者的混合问题带有时间窗的车辆调度问题统称为VRPTW(Vehicle Scheduling Problem with Time Windows)问题。Solomon和 Desrosiers首次对有时间窗约束的VRP问题进行求解。在国内李军，郭耀煌等学者对物流配送车辆优化调度理论与方法进行了深入的研究，为本文的研究提供了一定的理论依据。国内很多学者采用蚁群算法解决VRP问题，王海星等学者发表了“蚁群算法解决有时间窗的车辆优化调度问题研究”，该文介绍了如何运用改进的蚁群算法去优化带时间窗的车辆调度问题，对本文的实例有很大的借鉴意义。

1 飞机加油车辆的分类及功能

运输飞机加油作业都由加油车完成，加油车有两种类型，即管线加油车和油罐车。管线加油车用于对近机位航空器提供航空用油，油罐车用于对远机位的航空器提供航空用油。所谓进机位是指靠近航站楼的停机位，顾名思义远机位就是远离航站楼的停机位。进机位地底铺有输油管道，飞机加油时只需要管线加油车将管道中的航空用油抽出输送到飞机油箱中，而远机位地下没有输油管道，因此需要油罐车为该位置飞机提供航空用油。

管线加油车是以大流量将地井中的航空燃油安全、快速地输入飞机油箱。在输油的同时过滤燃油中的杂质、灰尘和水分，并精确地计量输油量。管线加油车还具有压力控制装置，可使输油过程中压力限制在安全范围内。它是飞机在进机位加油所使用的加油车辆。

油罐车又称流动加油车，具有吸油、泵油，多种油分装、分放等功能。运油车专用部分由罐体、取力器、传动轴、齿轮油泵、管网系统等部件组成。管网系统由油泵、三通四位球阀、双向球阀、滤网、管道组成。它是飞机在远机位加油所使用的车辆。本文将建立油罐车的调度模型并对其进行仿真计算。

2 油罐加油车辆调度数学模型

2.1 油罐加油车辆调度模型变量的定义 加油车辆行驶的基本过程可理解为每辆加油车从油库出发沿着一条行车路线对等待加油的飞机提供加油服务后返回油库。每辆加油车可以对多架飞机提供加油服务但每架飞机只能由一辆加油车为其加油。对于油罐车，其载油能力有限，所以为飞机提供的油量不能超过这个限制，设定所有油罐车的容量为Q。对于其他各个变量定义如下：

将油库编号为0，各个停机位编号为1，…，l。停机位及油库均以点i（i=0，1，…，l）来表示。定义Ti为加油车在飞机处i的工作时间，则T0表示加油车在油库的准备时间。定义 k（k=1，2，…，K）为各个加油车的编号。

定义cij为加油车辆由点i行驶到点j的成本。dij为加油车辆由点i行驶到点j的距离。tij为加油车辆由点i行驶到点j所需的时间。qi为点i飞机所需求的油量。Ti为加油车辆在点i完成加油任务所需要的时间。Si为加油车辆到达点i的时间，因此Si+1=Si+Ti+ti，i+1。飞机加油车辆的调度是一个带有时间窗的模型，即加油任务的开始时间需要在一定的时间范围内，设这个时间范围为[ETi，LTi]。其中ETi为加油任务i的允许最早开始时间，LTi为加油任务i的允许最晚开始时间。如果加油车辆在ET之前到达i，则会产生等待成本，如果加油车辆在LTi之后到达i，则会产生延误会造成损失。设定一个罚函数Pi（Si），其具体定义为：

其中m，n为惩罚系数。定义hi为判断该点飞机是否产生延误，当改点飞机发生延误时其值为1，当该点飞机没有延误则其值为0。

2.2 油罐加油车辆调度最优化数学模型 根据一般的车辆调度模型首先建立基本目标函数：

其中：

考虑油罐加油车辆调度是带有时间窗的模型，只有在时间窗内进行加油作业时才不会产生惩罚，否则会造成成本损失，故建立时间窗目标函数：

由以上分析得出最终目标函数：

约束条件设定：定义一个参数y，用以判断该点的飞机是由哪辆油罐加油车提供航空用油。

油罐车的容量Q为固定值，因此根据一般车辆调度约束条件定义飞机油罐加油车辆调度的模型约束为：

3 油罐加油车辆优化调度的蚁群算法

3.1 蚁群算法构造 车辆调度模型的解决方法可以分为两类，一类是优化算法，一类是启发式算法。而启发式算法中的群体智能仿生算法在解决这类问题时有其独到之处。本文将用蚁群算法解决该车辆调度问题，并用matlab进行仿真计算。蚁群算法是通过对蚂蚁群在巢穴与食物间的路径选择的模拟，来解决现实的NP难题。其重要的参数为（第k只蚂蚁的状态转移概率）；τij（信息素浓度）；ηij（启发因子）；ρ（信息素挥发系数）；α，β（重要度因子）。根据本文的模型对其进行如下定义：

其中：dij为停机位i点到j点之间的距离；μij称为节约值，其表示两点直接相连比两点分别与加油中心相连距离的节约量；δij是反应满足时间窗程度的变量，w1+w2=1；信息素更新策略则按公式（15），（16）进行。

3.2 具体实现步骤

①信息初始化，将蚂蚁置于加油中心位置，即禁忌表tabuk第一列位于初始位置。

②每个蚂蚁按概率移动一步，确定待访问点集allowedk。

③按公式计算状态转移概率p，按状态转移概率确定转移节点j，并将j添加到tabuk末尾。

④判断线路上加油量是否小于车辆负载Q，是则接下一步，否则跳转第⑥步。

⑤判断时间窗是否满足要求，是则将点j加入到tabuk中，并计算路径长度及其成本，统计车辆数并跳转第②步。否则跳转第⑥步骤。

⑥判断allowedk表，若allowedk表为空则转下一步，否则从表中获取时间最早的点，并转第③步。

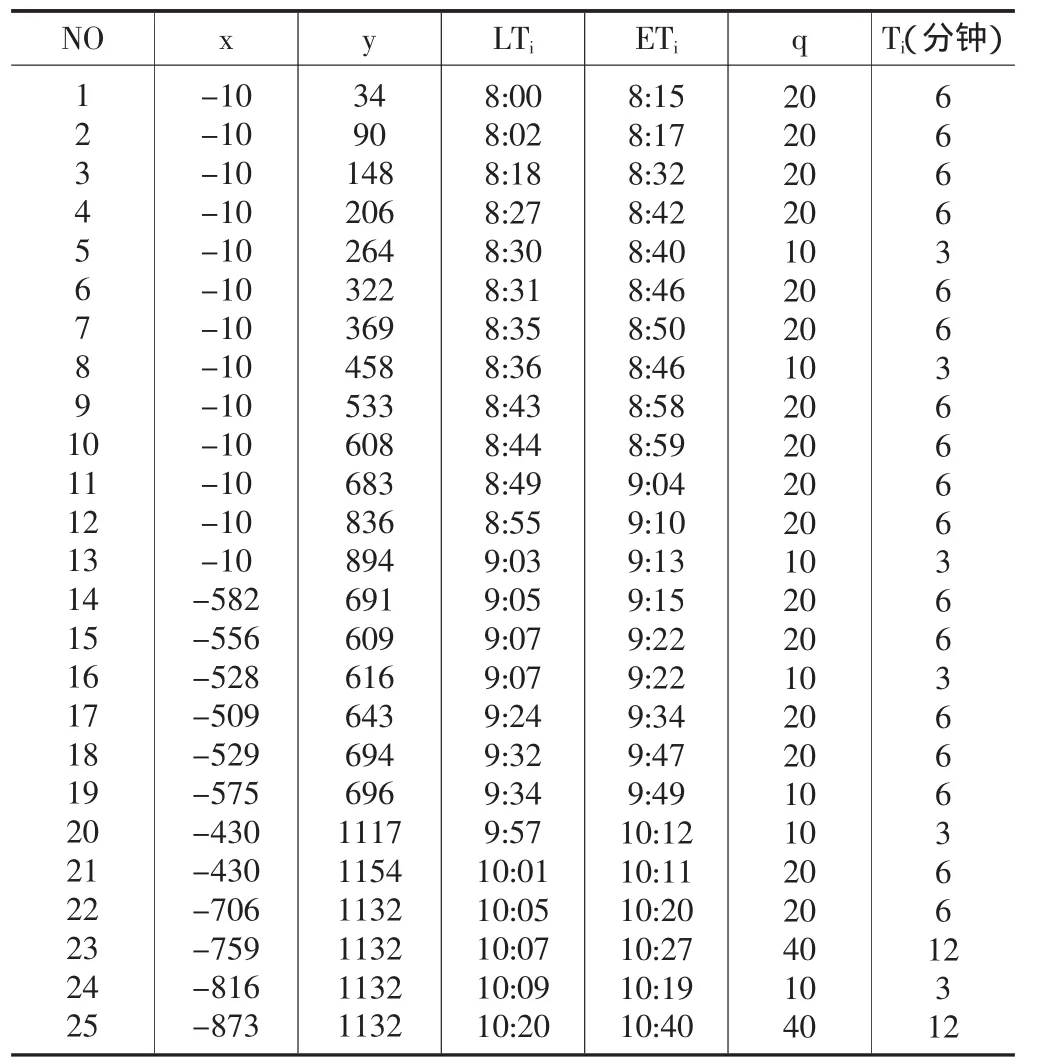
表1 远机位待加油飞机信息表

图1 油罐加油车优化路径图

⑦更新全局信息素，更新最好最差蚂蚁。

⑧禁忌表清零，输出结果。

3.3 算例分析 以某机场油罐加油车优化调度为例，设置加油中心为原点坐标，x表示停机位的横坐标，y表示停机位的纵坐标ETi，LTi分别表示飞机加油作业时间窗的上限和下限，q表示该飞机需要的油量，Ti表示该飞机加油所需要的时间，具体数据见表1。

设置油罐车加油车容量为 80，α=1，β=2，ρ=0.5，N=200；以加油成本为目标函数，用matlab编程工具使用蚁群算法最终得到油罐车最优路径图如图1所示，其优化路径为 0-1-2-3-4-0，0-5-6-7-8-9-0，0-10-11-12-13-0，0-14-15-16-17-19-0,0-18-22-23-0,0-20-21-24-25-0，共需要5车次油罐车去完成该仿真问题的加油任务。

4 结论

飞机加油作业是停机坪地面保障作业的重要环节，文中所引用的车辆调度的模型概括的模拟了飞机加油车辆的优化调度，并用蚁群优化算法对该模型进行仿真计算，得到了比较理想的结果，这对实际中飞机加油作业的操作具有一定的借鉴意义。

[1]郭耀煌，李军.车辆调度问题的研究现状评述[J].西南交通大学学报，1995，30（4）：376-382.

[2]王海星，王德占，申金升.蚁群算法解决有时间窗的车辆优化调度问题研究[J].物流技术，2006,11：37-40.

[3]段海滨等.蚁群算法原理及其应用[M].科学出版社，2005（12）.