基于主瓣杂波高效配准的机载非正侧视阵雷达STAP算法研究
王 杰 沈明威 吴 迪 朱岱寅
①(河海大学计算机与信息工程学院 南京 211100)
②(南京航空航天大学电子与信息工程学院 南京 210016)
1 引言
机载雷达是现代战场动目标探测的重要传感器。但机载雷达下视工作,杂波谱严重展宽,导致慢速目标检测性能下降。1973年,Reed和Brennan提出了在空时2维平面自适应抑制杂波的空时自适应处理(STAP)的概念[1,2],STAP技术能显著提高机载雷达对慢速目标的探测性能[3]。近40年来,STAP一直是雷达信号处理领域的研究热点,也是新一代机载雷达杂波抑制的关键技术。
STAP技术的研究已由正侧视阵雷达逐渐转向其他各种阵面构型,比如前视阵,斜侧视阵和共形阵雷达[4]。由于非正侧视阵雷达杂波特性明显不同于正侧视阵,因此基于正侧视阵提出的STAP算法就不一定适合非正侧视阵雷达。由于非正侧视阵雷达,其杂波在近程随距离严重非平稳,此时如果直接利用相邻距离单元来估计杂波协方差矩阵,必然导致STAP滤波器的凹口严重展宽。
解决机载非正侧视雷达杂波距离空变特性的主要方法是对杂波谱进行配准补偿,如多普勒频移(Doppler Warping,DW)[5]补偿,角度多普勒补偿(Angle Doppler Compensation,ADC)[6,7],自适应角度多普勒补偿(Adaptive Angle Doppler Compensation,A2DC)[8]等。但上述算法的补偿参数一是根据雷达系统参数直接计算,误差下补偿性能比较差[9,10];二是采用基于空时子孔径平滑后的MVDR谱估计补偿系数,但子孔径平滑降低了MVDR谱分辨率且运算量极大。本文采用时空级联方法,对主杂波所在多普勒单元采用稀疏重构技术,高效高精度估计主杂波2维频谱坐标,然后采用自适应配准及后续的3DT[11]进行杂波抑制。
全文结构如下,第2节分析机载非正侧视阵雷达的杂波特性,第3节研究主杂波高效自适应配准算法,第4节给出仿真计算结果,最后全文结论。
2 机载非正侧视阵雷达杂波特性
机载雷达几何构型如图1所示。假定雷达天线为均匀线阵,载机以速度v沿X轴飞行,β,α分别为散射体P相对于天线轴向和速度v方向的夹角。考虑非正侧视阵,ψ为偏航角,θ和φ分别为方位角和俯仰角。载机飞行高度为H,天线阵元个数为N,一次相干处理间隔内时域脉冲数为K,则第l个距离单元接收杂噪信号为:
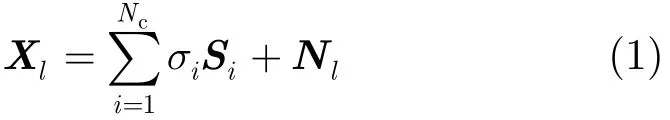
式中σi为该距离环第i个独立杂波散射源的信号幅度,Si为该散射源空时导引矢量,Nc为独立杂波散射源个数,Nl为系统噪声。对第i个独立杂波散射源P,

其中⊗为Kronecker积,Ssi,Sdi分别对应时域导引矢量和空域导引矢量,即
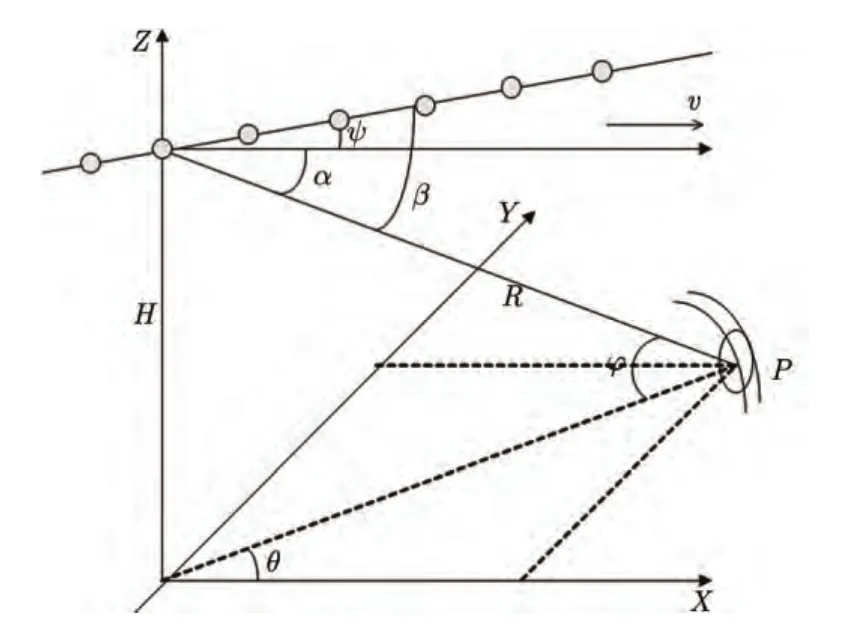
图1 机载雷达杂波几何关系Fig.1 Geometry of nonsidelooking array radar
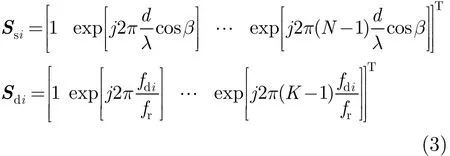
式中d为阵元间距,λ 为雷达波长,fdi=(2v/ λ)⋅cosα为散射体P的多普勒频率,fr为脉冲重复频率(PRF)。
在非正侧视条件下,杂波空时分布轨迹为[1]:
式中fc=(fdλ)/(2v)=cos α。正侧视条件下,即ψ=0°时,杂波轨迹为fc~cosβ平面内斜率为1的直线。前视条件下,即ψ=90°时,杂波轨迹为fc~cosβ平面内一簇半径为cosφ的同心圆。当0°<ψ<90°时,由式(4)可知杂波谱为一簇斜椭圆。如果忽略天线后向辐射的影响,实际杂波谱是椭圆的一半。
假定载机高度H=8 km,图2分别给出了斜距为9 km,10 km,15 km,100 km和200 km时杂波谱的2维分布轨迹。可见,机载非正侧视阵雷达杂波谱具有距离空变特性,且近距离单元变化快,远距离单元变化较慢。STAP要求训练样本具有独立同分布特性,因此机载非正侧视阵雷达的杂波距离空变特性必然引起STAP杂波抑制性能的下降。
3 主瓣杂波高效自适应配准算法
由前述分析可知:机载非正侧视阵雷达杂波的距离空变特性将导致相邻距离单元估计的2维杂波谱严重展宽和后续STAP对慢速目标检测性能的下降。对各距离单元主瓣杂波进行配准可有效改善近程杂波的距离空变性。考虑到时域脉冲数K一般远大于空域阵元数N,本文提出了时空级联主瓣杂波高效自适应配准方法,包括多普勒频率估计、空间频率估计和2维自适应配准。图3给出了该算法的信号处理流程。
3.1 主杂波多普勒频率估计
主杂波多普勒频率与天线主波束指向紧密相关,因此,首先对各阵元输出信号进行数字波束形成(DBF),得到接收和波束。假定接收和波束权值为WΣ,将第l个距离单元接收信号Xl逐脉冲排列,即:
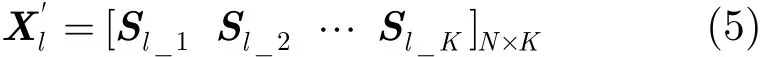
式中Sl_i为该距离单元在第i个脉冲各阵元接收信号矢量,则和波束输出信号为:

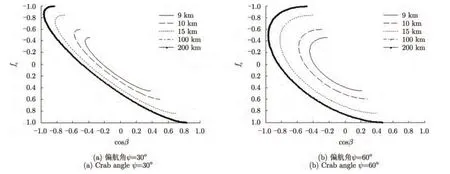
图2 机载非正侧视阵雷达杂波谱分布轨迹Fig.2 Doppler-angle trajectories of different range cells for nonsidelooking array radar
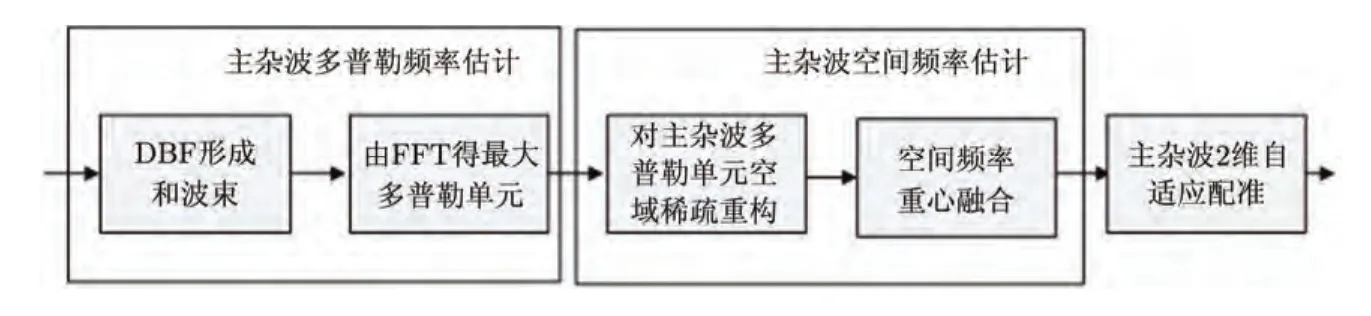
图3 主杂波高效自适应配准算法流程图Fig.3 The flow of mainlobe clutter compensation
经发射、接收波束天线方向图双程调制后,主杂波就对应最大的多普勒单元输出。因此,对和波束信号进行快速傅里叶变换(FFT),即:
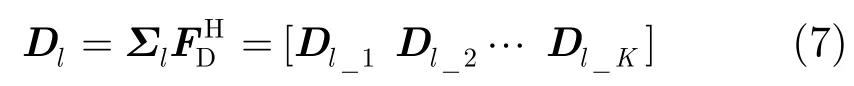
式中FD为FFT变换矩阵,Dl_i为该距离单元第i个多普勒单元和波束输出信号。最大输出的多普勒单元即对应主杂波的多普勒频率。
3.2 主杂波空间频率估计
在得到主杂波多普勒频率后,需进一步估计其空间频率。由于空域阵元数远小于时域脉冲数,对空域信号也直接采用 FFT获得的 2维傅氏谱副瓣高、分辨率差,无法有效估计主杂波的空间频率。为获得高分辨率频谱估计,稀疏重构技术被引入阵列DOA[12]和STAP的2维杂波谱估计。文献[13-15]提出对空时信号直接采用稀疏重构技术估计高分辨率2维空时谱,即:
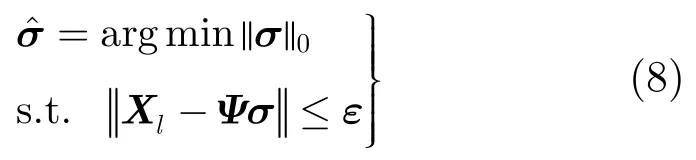
式中矢量σ为第l个距离单元Xl在角度-多普勒域的幅度分布,即对应 2维空时谱,Ψ为由空时导引矢量构成的一组超完备基,其维数为 NK×NsNt,Ns,Nt分别为角度域和多普勒域的量化单元。在Ns×Nt的 2维平面稀疏重构角度-多普勒谱,其运算量约为。文献[13]取Ns=6N,Nt=6K,因此,在空时域直接稀疏重构2维空时谱运算量极其庞大,严重限制了实时处理。
主杂波空间频率仅需对最大多普勒单元输出信号进行空域稀疏重构,即:
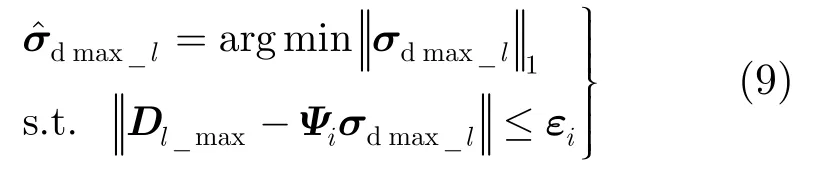
式中采用l1范数约束主杂波信号的空域稀疏性,Ψi为由空域导引矢量构成的一组超完备基,Dl_max为第l个距离门最大多普勒单元输出信号,σdmax_l为第l个距离门主杂波在空间频率域的幅度分布。将式(9)与式(8)相比,Ψi的维数由 NK×NsNt锐减为 N×Ns,因此相比全空时域稀疏重构本文算法运算量明显下降。
逐多普勒单元进行空域稀疏重构即可获得杂波的2维空时谱。假定 N=16,K=128,ψ=30°。图4给出了斜距10.5 km处距离单元的2维空时谱。可见,采用空域稀疏重构有效避免了空域傅氏谱的高副瓣和低分辨率,因而能准确估计主杂波的空间频率。由于稀疏重构获得的空间谱存在不连续性,本文采用重心融合法[16]提高主杂波空间频率的估计精度。
3.3 主杂波2维自适应配准
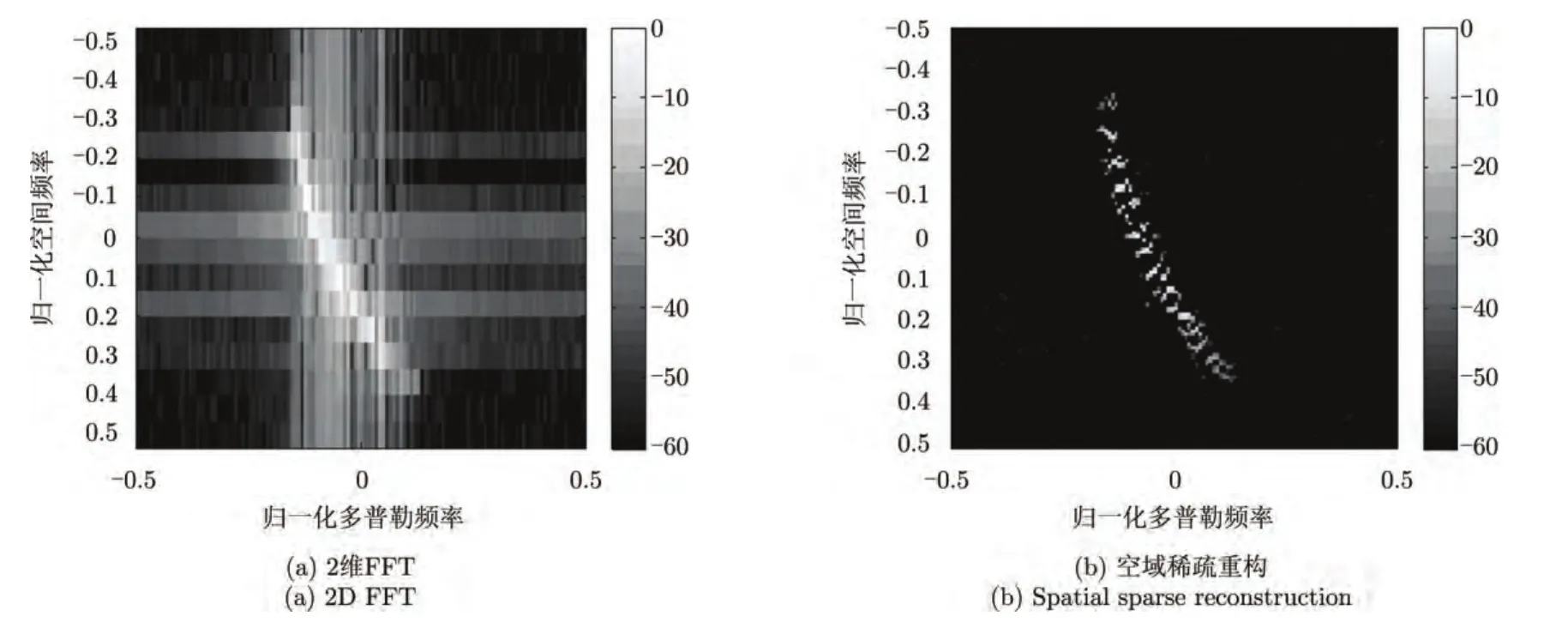
图4 斜距10.5 km杂波2维角度-多普勒谱Fig.4 The clutter angle-Doppler spectrum image with 10.5 km slant distance
采用前述时空级联算法可准确估计近程各距离单元主瓣杂波的多普勒频率和空间频率。因此,可将用于计算 STAP权值的相邻距离单元以检测距离单元的主瓣杂波为基准,分别进行2维自适应配准。
假定检测距离单元主杂波的频谱中心为(fs,0,fd,0),第l个相邻距离单元主杂波频谱中心为(fs,l,fd,l),则两距离单元主瓣杂波谱的多普勒频率偏移和空间频率偏移分别为:

因此,对第l个相邻距离单元而言其主杂波多普勒频率补偿因子和空间频率补偿因子分别为:
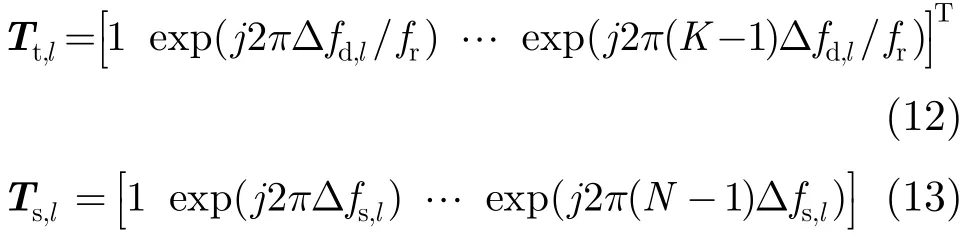
第l个相邻距离单元经主瓣杂波配准后,其输出信号为:

经主杂波配准补偿后,各距离单元杂波谱的距离空变性得到了有效改善,后续可采用经典的3DT降维STAP算法进行杂波抑制。3DT算法详见参考文献[11]。
4 性能分析
下面通过计算机仿真试验来验证本文方案的性能。机载非正侧视阵雷达系统仿真参数如表1所示,均匀线性阵列阵元数N=16,时域脉冲数 K=128,载机偏航角ψ=30°。仿真实验中,以第350个距离单元为基准(斜距为10.5 km),对前后相邻50个距离单元进行主杂波配准,并计算相应的 3DT改善因子。
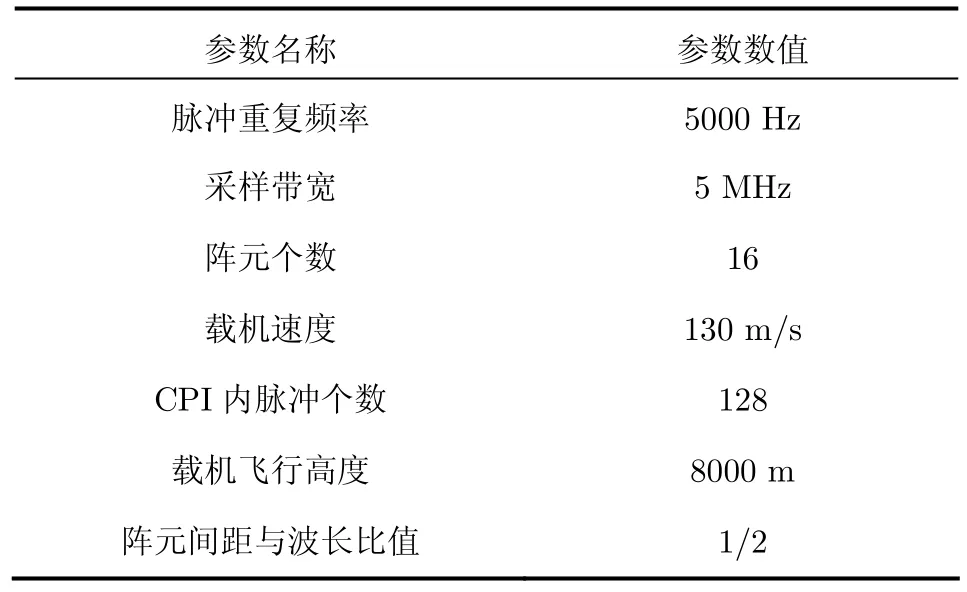
表1 雷达系统仿真参数Tab.1 Simulation parameters for radar
图5分别给出了主杂波配准前后各距离单元主杂波空时频谱的中心位置。如图 5(a),由于非正侧视阵雷达杂波谱的距离空变性,各距离单元主杂波频谱中心随距离发生迁移变换。采用本文方法经 2维自适应配准后,各距离单元主杂波频谱中心位于相同位置如图5(b)所示。
3DT由相邻距离单元估计检测单元的自适应权值。因此各距离单元2维空时谱分布越一致,其杂波距离非平稳性越小,3DT改善因子的凹口相应变窄。这里采用前述 3.2节介绍的逐多普勒单元空域稀疏重构估计各距离单元的高分辨率2维空时谱。图6(a)中是未配准补偿前第301和第350距离单元的2维空时谱,图6(b)为采用本文方案进行主杂波配准后第301和第350距离单元的2维空时谱。相比图 6(a),配准后主杂波区多普勒频谱带宽明显减小,因此估计的3DT权值应用于STAP后具有更好的慢动目标检测性能。
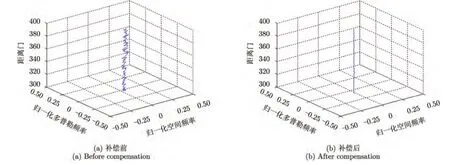
图5 杂波谱中心随距离单元迁移图Fig.5 Spectral Centers migration over range
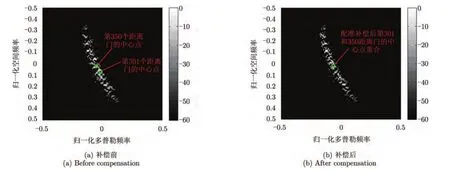
图6 不同距离单元杂波空时谱Fig.6 Spectrum of different range cells
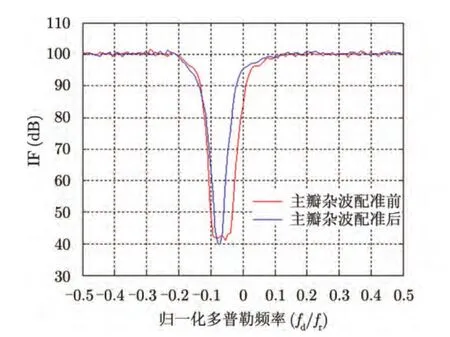
图7 杂波补偿前后数据的3DT算法的改善因子Fig.7 IF of 3DT algorithm before and after compensation
定义改善因子(IF)为输出信杂噪比与输入信杂噪比的比值[1]。图7分别给出了以第350个距离单元为中心,进行配准计算的改善因子曲线。计算结果表明:对各距离单元进行主杂波配准后,有效改善了杂波谱距离空变性,主杂波扩散区(取杂波中心多普勒单元前后 12个多普勒单元进行统计)改善因子平均提高了约 18 dB。本文提出的主杂波高效自适应配准算法运算量仅为3DT运算量的10%,运算效率显著优于MVDR谱估计。
5 结论
本文针对机载非正侧视阵雷达,研究基于主瓣杂波高效自适应配准的STAP算法。文中提出了时空级联的主杂波补偿参数估计方法,并采用稀疏重构技术高效高精度估计主杂波空间频率。仿真实验表明,经主杂波配准后,近程杂波的距离空变性得到了显著改善,主杂波区STAP改善因子提高了约18 dB。仿真结果有效验证了本文方案的有效性,且算法运算效率高,易于工程实施。
[1]Klemm R.Principles of Space-time Adaptive Processing[M].London: The Institution of Electrical Engineers,2002: 1-116.
[2]Brennan L E and Reed I S.Theory of adaptive radar[J].IEEE Transactions on Aerospace and Electronic Systems,1973,9(2): 237-252.
[3]Reed I S,Mallett J D,and Brennan L E.Rapid convergence rate in adaptive arrays[J].IEEE Transactions on Aerospace and Electronic Systems,1974,10(6): 853-863.
[4]Ries P,Lapierre F D,and Verly J G.Geometry-Induced range-dependence compensation for bistatic STAP with conformal arrays[J].IEEE Transactions on Aerospace and Electronic Systems,2011,47(1): 275-294.
[5]Borsari G K.Mitigating effects on STAP processing caused by an inclined array[C].Proceedings of the 1998 IEEE Radar Conference,Dallas,1998: 135-140.
[6]Fallah A and Bakhshi H.Extension of Adaptive Angle-Doppler Compensation (AADC) in STAP to increase homogeneity of data in airborne bistatic radar[C].2012 Sixth International Symposium on Telecommunications (IST),Tehran,2012: 367-372.
[7]赵军,朱兆达.非正侧视阵列机载雷达多空间角补偿算法[J].航空学报,2010,31(11): 2216-2221.Zhao Jun and Zhu Zhao-da.A multiple space angle compensation method for airborne radar with non-side-looking uniform linear array[J].Acta Aeronauticaet Astronautica Sinica,2010,31(11): 2216-2221.
[8]田斌,朱岱寅,朱兆达.一种快速自适应角度-多普勒补偿算法[J].航空学报,2011,32(9): 1705-1713.Tian Bin,Zhu Dai-yin,and Zhu Zhao-da.A fast adaptive angle Doppler compensation method[J].Acta Aeronautica Et Astronautica Sinica,2011,32(9): 1705-1713.
[9]郑世超,宋红军,刘亚波,等.广域监视动目标检测模式下动目标快速定位误差分析[J].雷达学报,2103,2(4): 445-453.Zheng Shi-chao,Song Hong-jun,Liu Ya-bo,et al..Error analysis of fast moving target geo-location in wide area surveillance ground moving target indication mode[J].Journal of Radars,2103,2(4): 445-453.
[10]刘振,魏玺章,黎湘.一种新的随机PRI脉冲多普勒雷达无模糊MTD算法[J].雷达学报,2012,1(1): 28-35.Liu Zhen,Wei Xi-zhang,and Li Xiang.Novel method of unambiguous moving target detection in pulse-doppler radar with random pulse Rrepetition interval[J].Journal of Radars,2012,1(1): 28-35.
[11]Dipietro R.Extended factored space-time processing for airborne radar systems[C].Proceedings of the 26th Asilomar Conference on Signals,Systems,and Computing,Pacific Grove,CA,1992: 425-430.
[12]Hu Nan,Ye Zhong-fu,Xu Xu,et al..DOA estimation for sparse array via sparse signal construction[J].IEEETransactions on Aerospace and Electronic Systems,2013,49(2): 760-773.
[13]孙珂,张颢,李刚,等.基于杂波谱稀疏恢复的空时自适应处理[J].电子学报,2011,39(6): 1389-1393.Sun Ke,Zhang Hao,Li Gang,et al..STAP via sparse recovery of clutter spectrum[J].Acta Electronica Sinica,2011,39(6): 1389-1393.
[14]Honglin W and Shu W.Adaptive sparsity matching pursuit algorithm for sparse reconstruction[J].IEEE Signal Processing Letter,2012,19(8): 471-474.
[15]Ali C G,Volkan C,and James H M.Bearing estimation via spatial sparsity using compressive sensing[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(2): 1358-1369.
[16]吴洪,王永良,陈建文.基于频心法的STAP非均匀检测器[J].系统工程与电子技术,2008,30(4): 606-608.Wu Hong,Wang Yong-liang,and Chen Jian-wen.Nonhomogeneous detector for STAP based Oil spectral center frequency method[J].Journal of Systems Engineering and Electronics,2008,30(4): 606-608.

