模块化多电平换流器不对称桥臂的环流稳态分析

韩少华，梅 军，郑建勇，吉 宇，杜晓舟

（东南大学 电气工程学院，江苏 南京 210096）

0 引言

模块化多电平换流器MMC（Modular Multilevel Converter）最早是由慕尼黑联邦国防军大学的Marquardt和 Lesnicar等人提出的[1]，具有多方面的优势，如整流和逆变状态四象限运行、可满足不同等级电压的模块化结构、可满足高压大功率需求、可不接变压器以及冗余化设计等[2-7]，因此近期得到了越来越广泛的发展和研究。

然而，MMC的桥臂环流问题始终制约着MMC的发展[8-10]。桥臂环流是由于上、下桥臂能量分布不均匀导致的，不仅可能引起波形的畸变影响输出质量，还会增加器件的损耗，提高对开关器件的要求。目前已有大量的研究显示，对于上、下桥臂对称的MMC而言，其环流的成分为直流量和2次分量[11-13]。

但实际上，桥臂的电阻、电感是很难做到完全相等的，总会有一些误差难以避免地存在，这势必会导致环流的成分更加复杂化，以往的理论也难以对此情况进行分析。因此有必要对桥臂阻感不对称情况下的MMC环流成分以及环流表达式进行研究。

本文从桥臂阻感不对称的MMC拓扑结构出发，通过子模块悬浮电容电压的变化规律，从时域角度构建描述环流特征的二阶微分方程。在稳态情况下忽略微分方程的通解，通过近似处理方法求得微分方程的特解，其特解可以有效地描述环流的稳态特性，不仅指出此时环流的主要成分为直流分量、1次分量和2次分量，还给出了此时环流的稳态表达式。通过MATLAB/Simulink平台对该理论的正确性和有效性进行仿真验证，理论环流波形与实际仿真符合完好，在桥臂阻感不对称的时候，其稳态环流表达式可准确完好地描述出环流的稳态特征。

1 MMC的拓扑原理

MMC的电路拓扑结构如图1所示，每相由一系列参数相同的子模块（SM）串联得到[14-16]。单个SM结构如图2所示，其为2个开关管与电容并联，相当于1个独立的直流源。每一个SM的参数均是相等的，因此每时刻接入电路的子模块数量必须恒为N，这样保证了上、下桥臂电压之和等于直流侧电压，从而利于电容电压的平衡稳定。

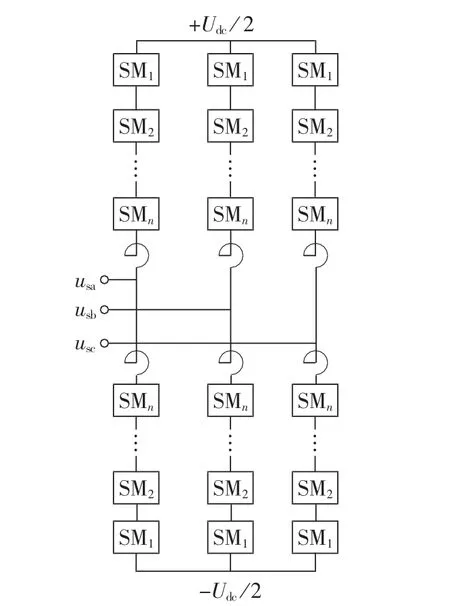
图1 MMC的拓扑结构Fig.1 Topology of MMC

图2 子模块的拓扑结构Fig.2 Topology of sub-module

通过SM结构中开关器件的开断，可以控制SM的输出电平。在系统正常工作状态下，每一个SM存在2种输出电平：当每个SM单元的IGBT1导通、IGBT2关闭时，SM输出为电容电压UC，表示其接入电路，为接入状态；当IGBT2导通、IGBT1关闭时，SM输出为0，为短路状态。因此，每个SM都可以输出UC和0这2种电平。

从交流侧看，各相的SM皆为串联在一起，因此其输出电压是各个SM输出状态的代数叠加结果。假设MMC每相上、下桥臂各有N个SM，且同时只接入N个，那么可输出N+1种电平。

2 MMC桥臂不平衡下的环流方程

本文采用的调制算法为N+1调制算法，其上、下桥臂脉冲信号互为反相，可以满足每时刻投入主电路的子模块数恒为N。

桥臂不对称情况下MMC的单相等效电路图如图3所示。图中，MMC电路中上、下桥臂各SM的电压简化为交流源uj1和uj2，开关器件的电阻一并归到桥臂的电阻上，MMC输出经负载阻抗后接地。故有：

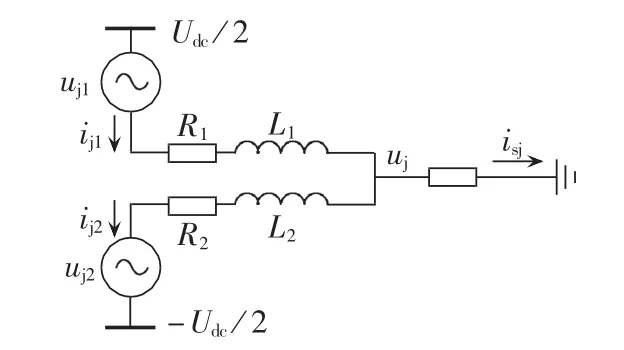
图3 MMC单相电路的数学模型Fig.3 Math model of MMC single-phase circuit

假定icj表示单相桥臂环流，则有：

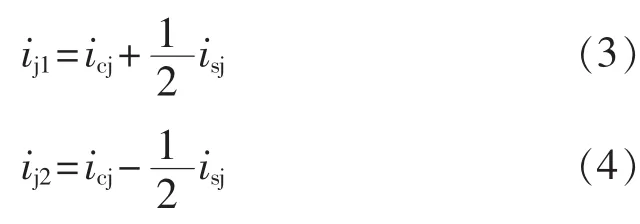
故由式（1）—（4）可有：

用uj∑表示接入主电路所有SM的电容电压之和：

uj∑为一个变化量，其值会随着开关信号变化而突变，但是在每个开关信号不变的小时间段内uj∑连续。对式（5）等号两边进行求导，可以得到：

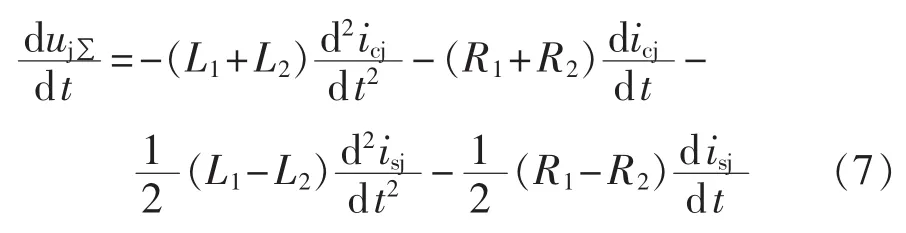
从另一方面分析电容电压总和uj∑，对于接入的第k个SM的电容电压有：

其中，ik为流过该SM悬浮电容的电流；u0k为该SM悬浮电容的初始电压；Sk为第k个SM的开关函数。

由此可以得到：

由于Sk为开关函数，由0和1构成，则可将整个过程分割为无数个小时间段，每个小段内N个SM的开关状态保持固定。由上文分析可得，在每一段内uj∑连续，则对每一个小时间段而言，段内均可以满足：

将上式中ik用上、下桥臂电流代替，则得：

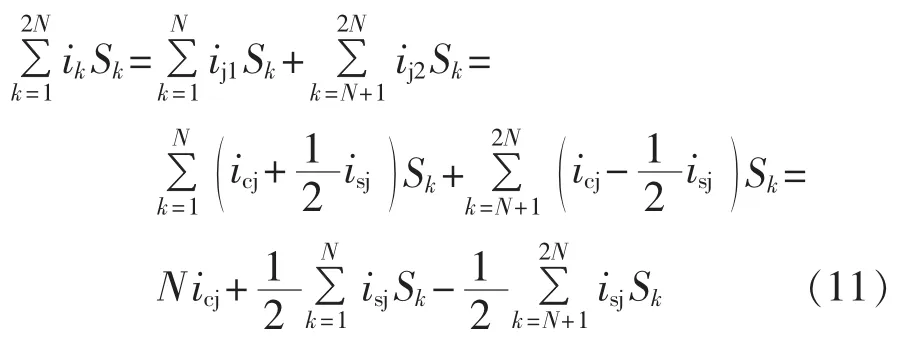
故由式（10）和（11）可得：

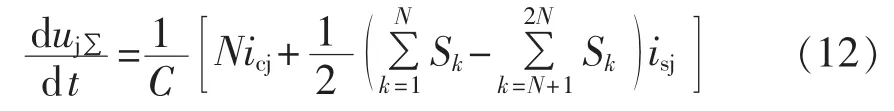
式（7）和式（12）分别从2种角度描述了电容电压总和与时间的微分关系，联立式（7）和（12）可得到方程：

方程（13）的等号右侧仅与各SM的开关函数和桥臂的输出电流有关，而与环流无关。方程本身为一个二阶常微分方程，其解描述了环流icj的存在形式。

方程（13）等号右侧的频率分量描述了稳态下环流的频率分量。当上、下桥臂对称时，右侧的基波分量为0，环流主要为直流和2次成分；当上、下桥臂不对称时，来自负载电流的基波分量则不可忽略。

3 桥臂环流方程的求解

对方程（13）进行求解，主要考虑通解和特解。方程的通解一般为衰减量，最终都将衰减为0，因此方程的通解部分仅仅描述环流初始状态的暂态特征，本文旨在研究环流的稳态特性，因此不作考虑。而对于方程的特解，具体的解法取决于方程等号右侧的表达式。若欲对方程进行求解，则必须对方程等号右侧的2个与环流无关的变量进行近似处理。

对于负载电流，一般而言，桥臂等效阻抗值与负载阻抗相比较小，即使桥臂阻抗不对称，对负载电流的影响也并不大。再加上负载电感的滤波作用，故而在稳态情况下，一般认为桥臂输出的负载电流可近似为标准正弦波形：

而对于开关函数，已知该开关函数除了基波外，含有大量的高次谐波，而高次谐波对环流方程特解的影响可以忽略。因此开关函数可直接近似取：

将式（15）代入方程（13），可以重写为：

不难解得方程的特解为：

至此，得到了稳态下方程的特解。特解中主要成分为直流量、1次分量和2次分量。式（17）也给出了桥臂不对称情况下环流的表达式，可通过该公式对桥臂环流进行理论计算。

4 环流方程稳态解的仿真验证

在MATLAB/Simulink下搭建MMC五电平单相逆变系统，参数如下：直流侧电压Udc=200 V，上桥臂电阻R1=0.4 Ω，上桥臂电感L1=2 mH，下桥臂电阻R2=0.2 Ω，下桥臂电感L2=1 mH，悬浮电容C=4.7 mF，调制比m=0.7，负载电阻为7 Ω，负载电感为20 mH。

图4为MMC稳态情形下的输出电压和输出电流。由图可见，输出的电压和电流波形规范。尤其是电流，基本保持为正弦波形，无明显畸变。图5给出了输出电流的谐波分析，可以看出，其THD为1.12%，畸变很小，1次分量之外其他频次分量均很小，也验证了上文对负载电流进行正弦基波近似的正确性。

图4 MMC输出电压与输出电流Fig.4 Output voltage and current of MMC

图5 MMC负载电流谐波分析Fig.5 Harmonic analysis of MMC output current

图6展示了不同桥臂电阻和电感配置下，环流的理论值和实际仿真波形的对比情况。由图6（a）可以明显看出，理论波形和实际仿真波形符合完好，仅有很小的相位误差，几乎可以重合。图6（b）与图6（a）的参数颠倒，但可以看出，仅仅是波形的形状发生变化，理论值和仿真值依然是几乎重合的。

图7展示了不同负载阻抗取值下的环流波形对比。此时取负载电阻为14 Ω，负载电感为40 mH。从图中可以看出，环流理论波形和实际仿真波形依旧是十分相近，依然只是存在一个微小的相位误差。

图8 展示了 R1=0.5 Ω、L1=3 mH、R2=0.2 Ω、L2=1 mH时，环流的理论波形和仿真波形的对比情况。由图可知，在桥臂电阻和电感发生变化时，环流的波形相应发生变化，但是理论波形和仿真波形依然可以符合完好，波形相差并不大。

图6—8在不同情况下对式（17）进行了验证，结果得到的理论波形总是和实际得到的仿真波形符合完好，有效地验证了公式给出的桥臂阻感不对称时环流表达式的正确性。

实际上，波形之所以总是存在误差，是因为在公式推导中，存在着近似处理，如将负载电流默认为标准基次正弦波。实际上，桥臂电阻、电感不对称情况会或多或少对输出的波形质量产生影响，因而带来相应的谐波。这也解释了当上桥臂电阻、电感变大时，误差也相应有所增大的原因。

图6 环流的理论波形与仿真波形对比Fig.6 Comparison of circulating current between theoretical and simulative waveforms

图7 RL=14 Ω、LL=40 mH时环流波形对比Fig.7 Comparison of circulating current waveform when RL=14 Ω，LL=40 mH

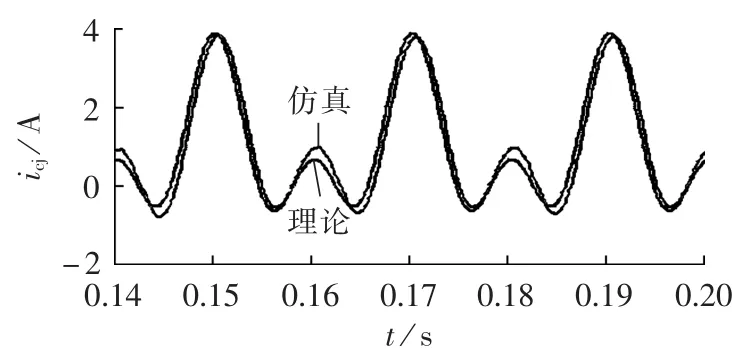
图8 R1=0.5 Ω、L1=3 mH、R2=0.2 Ω、L2=1 mH 时环流波形对比Fig.8 Comparison of circulating current waveform when R1=0.5 Ω，L1=3 mH，R2=0.2 Ω，L2=1 mH

5 结论

本文从桥臂阻感不对称的MMC拓扑结构出发，通过SM悬浮电容电压的变化规律，从时域角度构建描述环流特征的二阶微分方程。在稳态情况下忽略微分方程的通解，通过近似处理方法求得微分方程的特解，其特解可以有效地描述环流的稳态特性，不仅指出此时环流的主要成分为直流分量、1次分量和2次分量，还给出了此时环流的稳态表达式。

经仿真验证，该理论分析得到的环流波形与实际仿真得到的环流波形符合完好，在桥臂电阻、电感不对称的时候，其稳态环流表达式可准确完好地描述出环流的稳态特征，为实际中MMC参数选择问题提供有效的理论支撑。

然而本文采用的负载电流的基波正弦近似处理方案，实际上并不适用于所有场合，因为在某些桥臂阻抗不对称非常严重的情况下，负载电流势必会产生严重畸变，该近似方案就不能成立。这种情况下环流方程（13）的等号右侧必须另行处理，这也将是笔者下一步的研究目标。