模块化多电平换流器的电容电压平衡方法

薛 畅，申 科，纪延超，江滨浩

（哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001）

0 引言

近年来，多电平技术已逐步取代多重化技术和串联开关技术，成为柔性输电工程的首选[1-2]。由Marquardt R于2001年提出的模块化多电平换流器MMC（Modular Multilevel Converter）是多电平技术的一大飞跃[3-11]，由于其子模块为半桥式斩波电路，故亦被称为半桥式级联换流器。MMC独特的模块化结构和可扩展性使其可有效实现高电压等级下的电能变换。与链式逆变器不同，MMC不仅适用于无功补偿领域，由于具有公共直流侧，更加适用于背靠背和轻型直流输电系统[8-11]。自从MMC被提出后，子模块电容电压的平衡问题一直是研究热点。

目前多电平逆变器的调制方法主要有阶梯波调制、空间矢量调制、载波层叠调制和载波移相调制CPSPWM（Carrier Phase Shifted PWM）等。 其中CPSPWM由于具有谐波特性好、可控性强、易于实现、适用于模块化结构等优点，在多电平逆变器中得到了广泛应用[12]。当MMC采用上述前3种调制方法时，往往通过排序法或脉冲轮换法来平衡子模块的电容电压。排序法是根据电容电压对子模块进行排序，再由桥臂电流的方向决定各子模块的开关状态（需保证总的合成电压不变）[8-9]。排序法会造成额外的开关动作，导致开关损耗增大。脉冲轮换法是一种开环控制方法，其通过触发脉冲的轮换使同一桥臂中各子模块的投入时间基本相同，从而消除由调制方式引起的电压不平衡[13]。但在实际应用中，每个子模块的运行参数并不相同，所以脉冲轮换法不能从根本上解决问题。当MMC采用CPSPWM时，目前国内外文献所提出的平衡方法都是调制波增量法[14-16]，即在每个子模块的调制波上叠加若干增量，以实现对有功功率的合理分配，使各子模块的电容电压稳定在参考值附近。调制波增量法位于控制层，是宏观的，通常需要一个总控制环和若干针对各子模块的分控制环。当子模块的数目增大时，该方法的计算量急剧上升，且由于其改变了子模块的调制波，故会导致输出电压波形的畸变。

现提出一种采用CPSPWM的MMC的电容电压平衡方法。该方法位于调制层，不改变子模块的调制波，不影响输出电压波形，也不产生额外的开关损耗。

1 拓扑结构及工作原理

图1为三相MMC及其子模块的拓扑结构。图中MMC由6个对称桥臂组成，每个桥臂由n个子模块和1个限流电抗串联而成。Udc为MMC的直流母线电压。子模块为半桥式斩波电路，其电容电压应被稳定在Udc/n附近。一般而言，MMC的相电压需要有零电平，故n通常为偶数。

图1 MMC及其子模块的拓扑结构Fig.1 Topology of MMC and its sub-module

子模块有2种开关状态（不考虑死区），可由S表示，具体如表1所示。

表1 子模块的开关状态Tab.1 Switching states of sub-module

由此可知，当一个子模块处于切除状态时，其电容既不充电也不放电；处于投入状态时，其电容在桥臂电流大于0时充电，小于0时放电。

以a相上桥臂为例，第i个子模块的输出电压和电容电流可表示如下：

若忽略限流电抗的分压作用，a相电压（以直流母线中点为参考点）可表示如下：

Si需始终满足下式：

由式（2）可知，ua具有 n+1 个电平，即 -Udc/2，…，-2Udc/n，-Udc/n，0，Udc/n，2Udc/n，…，Udc/2。

子模块在调制过程中，其开关状态的变化规律如图2所示。

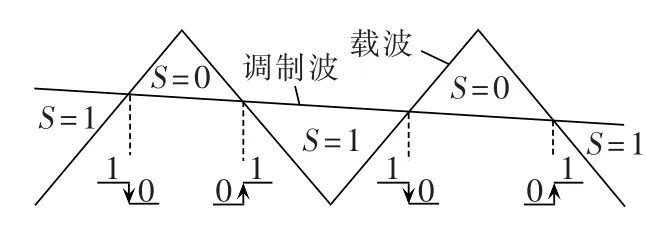
图2 开关状态的变化规律Fig.2 Law of switching state change

2 调制方式

CPSPWM是针对链式逆变器提出的，故适用于同是模块化结构的MMC。以a相为例，设调制波为ua*（即参考电压，范围通常为[-Udc/2，Udc/2]），归一化后上桥臂每个子模块的调制波为-u*a/Udc+1/2（取负是因为MMC具有反向性），下桥臂各子模块的调制波为 u*a/Udc+1 /2；调制比为 u*a的峰值与 Udc/2 之比；载波为极值是0和1的三角波；一个子模块对应一个载波，载波之间的相位互差360°/（2n）。

假设每个桥臂的子模块数为n=4，则上桥臂在1个工频周期内的调制结果如图3所示。第1个子图中，实线为上桥臂的调制波和载波，虚线为下桥臂的调制波和载波。

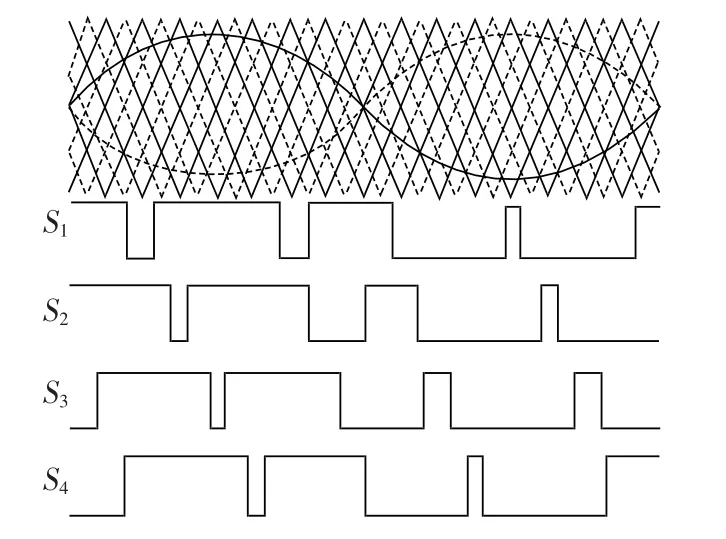
图3 上桥臂在1个工频周期内的调制结果Fig.3 Modulation results of upper arm within one grid period

3 电容电压的平衡方法

由式（2）可看出，同一桥臂中各子模块的开关状态可以互相交换，对输出电压不会产生影响。而子模块的开关状态是由调制波和载波比较得出的，同一桥臂中各子模块的调制波相同，所以它们的载波亦可互相交换。

本文提出的平衡方法要求所有载波（包括下桥臂）的顶点（对应1的点）均为采样点，故采样频率等于2n倍的载波频率。同样假设n=4，图4为上桥臂在2个采样周期内的调制结果。图中圆点代表采样点；T1、T2代表采样周期；粗实线为采样所得调制波；c1—c4、c5—c8分别为上桥臂和下桥臂的载波。

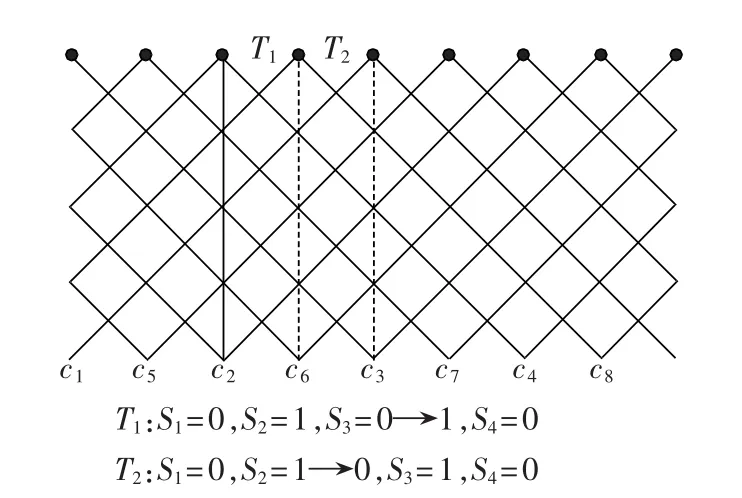
图4 上桥臂在2个采样周期内的调制结果Fig.4 Modulation results of upper arm within two sample periods

由图4可知，在一个采样周期内同一桥臂中各子模块的开关状态共有4种，分别是0、1、由0变至1（上升沿）和由1变至0（下降沿）。这4种状态中上升沿用于和“0”交换，下降沿用于和“1”交换，这样做可以保证过渡的平滑性，避免产生额外的开关损耗。在交换时，根据桥臂电流的方向，有如下4种情况，由此可得出该平衡方法的流程图如图5所示。图中，UC（MAX）、UC（MAX-1）分别是桥臂中最大和第二大的电容电压；UC（MIN）、UC（MIN+1）分别是桥臂中最小和第二小的电容电压，依此类推。

a.存在上升沿，桥臂电流大于0：对处于“0”状态的子模块的电容电压进行排序，选出电压最小的子模块。若该子模块的电容电压小于上升沿所在子模块的电容电压，则与之交换开关状态，即令其电容充电，否则不交换。

b.存在上升沿，桥臂电流小于0：对处于“0”状态的子模块的电容电压进行排序，选出电压最大的子模块，若该子模块的电容电压大于上升沿所在子模块的电容电压，则与之交换开关状态，即令其电容放电，否则不交换。

c.存在下降沿，桥臂电流大于0：对处于“1”状态的子模块的电容电压进行排序，选出电压最大的子模块。若该子模块的电容电压大于下降沿所在子模块的电容电压，则与之交换开关状态，即终止其电容的充电过程，否则不交换。

d.存在下降沿，桥臂电流小于0：对处于“1”状态的子模块的电容电压进行排序，选出电压最小的子模块。若该子模块的电容电压小于下降沿所在子模块的电容电压，则与之交换开关状态，即终止其电容的放电过程，否则不交换。

需要注意的是，上述开关状态的交换实际上是载波的交换，这种交换不是暂时的，当下一个采样周期来临时，将会在此次交换的基础上继续进行交换。

该方法不会造成额外的开关动作，但可能会导致开关频率分布不均匀，这是其唯一缺点。由于MMC在中高压领域中应用时效率通常很高（大于98%），自身损耗可忽略不计，故采用此方法不会对装置产生任何负面影响。另外，子模块的数目越大，可供交换的选择面就越广，平衡效果亦越好。

4 实验结果

为验证此方法的有效性，搭建了一台三相的MMC样机，参数如下：直流母线电压为240 V，桥臂子模块数n为4，子模块电容为3300 μF，限流电抗为2 mH，负载（每相）为 5 Ω+12.5 mH，载波频率为 1.2 kHz，调制比为0.9。

图6给出样机线电压波形，其为9电平PWM波。

图6 线电压波形Fig.6 Waveform of line voltage

图7为a相上桥臂子模块的电容电压波形。0.6 s前无平衡控制，故电容电压是分散的；0.6 s时加入平衡控制，0.2 s后各路电压均被稳定在60 V附近（之间无大幅波动），说明此方法有效可行。

图7 电容电压波形Fig.7 Waveforms of capacitor voltages

5 结论

本文提出的基于载波交换的方法可有效解决采用CPSPWM时MMC的电容电压平衡问题。相对于传统的排序法、脉冲轮换法以及调制波增量法，该方法具有诸多优势，如不改变调制波、不产生额外的开关损耗、计算量少等，且简单有效，可通过CPLD或FPGA轻松实现。