运行15万h后F12钢主蒸汽管道剩余寿命的预测与试验验证

黄维浩，张 瑞，唐松青，赵中平，彭行金

（上海发电设备成套设计研究院，上海 200240）

0 引 言

在未来相当长的一段时间内，我国以煤为主要能源的资源结构将不会改变，这就决定了火电在电源结构中的主导地位。据统计，到2012年12月底，中国电力的总装机容量已达到114 491万kW，其中火电占比超过70%，目前在役火电机组中累计运行时间超过设计寿命50%（10万h）的老设备占60%以上，因此针对这些设备的重要高温零部件开展剩余寿命研究，是当前电力行业的重要课题之一。

国外在此方面的研究已开展了几十年，并形成了一套较系统的评估方法，如美国研究与开发的火力发电厂主设备状态和剩余寿命评估技术已使美国电厂节约了3亿多美元［1］。近年来，国内外已提出了多种预测剩余寿命的方法［2－8］。

火电厂主蒸汽管道由于运行温度和运行压力均较高，是电厂四大管道中运行工况最恶劣、事故发生最多、同时也是最易老化的部件。因此对其剩余寿命进行评估是电厂状态检修、设备延寿最关心的工作之一。主蒸汽管道剩余寿命预测的方法有很多，如早期的蠕变寿命耗损法、疲劳寿命耗损法、蠕变疲劳交互作用法、以蠕变变形量为主要指标的θ函数法、C射影法、蠕变裂纹开裂和扩展寿命评估法、显微组织（老化）法等［9－19］。早期的蠕变寿命耗损法过于粗糙，评估误差较大；蠕变疲劳交互作用法比较适合大型转子的寿命评估；θ函数法原用于沉淀硬化合金，在进行一些假设和修正后可用于评估中低合金钢；C射影法在实际中应用较少；显微组织（老化）法不能进行持久强度试验，不能准确测定剩余寿命。国内通常采用上述评估方法中的某一种方法对主蒸汽管道进行剩余寿命评估，不能准确地综合评估主蒸汽管道材料强度和脆性等特性的变化，故而，作者分别应用时间－温度参数外推法（Larson-Miller参数法）和蠕变裂纹开裂与扩展寿命评估法，并参考材料的组织变化对某火电厂已运行27a、累计运行时间近15万h机组主蒸汽管道的剩余寿命进行了评估。该机组的设计蒸汽温度为550℃，压力为13.73MPa。

1 试样制备与试验方法

1.1 试样制备

主蒸汽管道材料为F12（X20CrMoV121）钢，由德国某钢管厂生产，其尺寸为φ273mm×26mm。该主蒸汽管系分别布置于甲乙两侧，共有56条焊缝，22只弯管。F12钢的主要化学成分（质量分数/%）：0.17～0.23C，10.0～12.5Cr，0.80～1.20Mo，0.30～0.80Ni，0.25～0.35V，≤0.030P，≤0.030S；主 要 力 学 性 能 如 下：Rm＝540～690MPa，Rp0.2≥490MPa，A＝17%。

取样前，先对整个主蒸汽管系进行了应力场的有限元计算，计算结果表明，该主蒸汽管系中乙侧第1只弯管承受的应力最大，该弯管的一次最大主应力为71.8MPa，最大二次主应力为31.0MPa，最大平均膜应力为60.8MPa；然后对管系不同位置处的硬度、壁厚和弯管不圆度进行现场普查，以便确定整个管系中受力最大、性能下降最多的管段，将该管段作为评估该主蒸汽管道剩余寿命的取样管。

现场检查结果表明，乙侧第1只弯管的硬度最低，为 208～217HB，壁 厚 正 常，为 25.0～25.4mm，不圆度最低，最大外径与最小外径之比为1.12。这说明该弯管的老化程度最大，与有限元应力计算结果一致，因而确定乙侧第1只弯管为该主蒸汽管道寿命评估的取样管段。

1.2 试验方法

在运行后取样弯管的外弧面环向截取试样，并在470，550，600℃及不同应力条件下进行持久强度试验，持久强度试验采用直径为10mm的圆形横截面标准持久试样，按GB/T 2039－1997《金属拉伸蠕变及持久试验方法》，在RD2-3型高温持久试验机上进行。

从取样弯管外弧面的切向取样制成带有预制裂纹尺寸为25mm×25mm×10mm的标准紧凑拉伸试样（预制裂纹长度a为10mm，裂纹到试样两端的距离H 为12.5mm），在RD2-3型蠕变试验机上按JB/T 8189－1999《汽轮机高温裂纹开裂与扩展速率试验方法》进行试验，试验设备的控温精度为±0.5 ℃，初始加载载荷分别为 100，110，120，130MPa·m1/2，试验温度为550℃。

根据GB/T 13298－1991《金属显微组织检验方法》，在NEOPHOT 21大型卧式光学显微镜（OM）上对取样弯管进行组织观察，同时线切割截取0.5mm的薄片，经机械研磨至0.05mm后，在MTD-1型双喷电解减薄仪上制成透射电镜试样，利用FEI TECNAL G2型透射电子显微镜（TEM）分析碳化物的分布与类型。进行组织观察和碳化物分析的试样均取自取样弯管的外弧面。

2 剩余寿命预测方法和计算模型

2.1 时间－温度参数法（Larson-Miller参数法）

应用Larson-Miller参数法来预测主蒸汽管道的剩余寿命时，通常是通过持久强度试验得出运行后材料的Larson-Miller参数曲线，再根据稳态运行工况下的温度、压力参数来计算材料的剩余寿命。但事实上主蒸汽管道在运行过程中承受压力波动、振动及其它附加应力，因此用稳态运行工况下的蒸汽参数来计算主蒸汽管道的剩余寿命不是很精确。利用等效运行应力（在已知累计运行时间ts内被评估材料所承受的当量应力）来建立主蒸汽管道材料

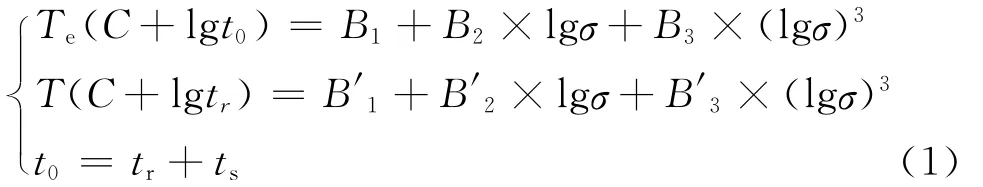
式中：Te为运行温度；C，B1，B2，B3为原始材料常数；B1′，B2′，B3′为运行后的材料常数；t0为材料的总寿命；tr为材料的剩余寿命；ts为材料已损耗的寿命，即累计运行时间；σ为主蒸汽管道承受的等效应力。的Larson-Miller参数方程，可以同时考虑到上述影响主蒸汽管道剩余寿命的其它因素。主蒸汽管道在承受各种工况下的累积损伤以及剩余寿命的计算模型见式（1）。

式（1）中第一个方程为原始材料持久性能的Larson-Miller参数方程，该方程可以通过积累的原始材料的持久数据来统计计算，第二个方程是运行后材料持久强度的试验结果。求解该方程组就可得出主蒸汽管道所承受的等效运行应力以及在等效运行应力条件下的总寿命和剩余寿命。

运用这种方法不但可以得到在不改变原有运行方式下被评估材料的使用寿命，还可以得到其它工况下（如降参数运行等）的剩余寿命。

2.2 高温蠕变裂纹开裂与扩展寿命法

主蒸汽管道有可能存在缺陷，同时材料长期运行后碳化物聚集长大，特别是晶界碳化物的聚集与长大，会严重削弱基体材料的性能，因此可以进一步通过评估材料的高温蠕变裂纹开裂时间与扩展速率来预测主蒸汽管道材料的剩余寿命。

高温蠕变裂纹开裂与扩展寿命的计算模型是基于连续损伤理论建立起来的。高温蠕变裂纹的开裂时间与初始裂纹尖端应力场强度因子关系符合式（2）：

式中：ti为开裂时间；A，m为材料常数；KI为裂纹尖端的应力场强度因子。

Larson-Miller参数法计算出的主蒸汽管道的等效运行应力是计算运行温度下蠕变裂纹开裂寿命的初始载荷。

蠕变裂纹从起始裂纹扩展到临界裂纹长度所需要的时间（即裂纹扩展寿命）可以通过式（3）和式（4）计算［20］：

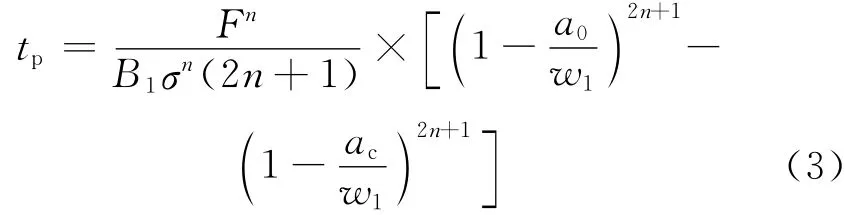
式中：tp为蠕变裂纹扩展寿命；F为几何形状系数；σ为等效运行应力；B1，n为材料常数，可根据裂纹扩展速率与裂纹尖端应力场强度因子的关系曲线得到；a0为初始裂纹长度；ac为临界裂纹长度；w1为主蒸汽管道的厚度；δcc为蠕变断裂韧度；A1为与工作应力以及温度有关的材料常数；ey为工作温度下屈服强度与弹性模量的比值。

蠕变裂纹开裂和扩展试验中裂纹长度的变化是通过试样两端的电位变化来测定的。当材料处于韧性状态时，蠕变裂纹在初始载荷的作用下须经过一定的孕育期后才能形成，表现在试样两端电位与时间的变化曲线上有台阶出现，当材料处于脆性状态时，试样两端电位与时间的曲线上没有台阶，其电位时间曲线是连续的。

由于高温蠕变裂纹的开裂时间远大于高温蠕变裂纹扩展到临界裂纹的时间，因此，在进行剩余寿命评估时，可以只考虑高温蠕变裂纹的开裂时间，而不考虑其扩展时间，但当主蒸汽管道存在裂纹等缺陷时，则必须要考虑蠕变裂纹的扩展时间。

3 剩余寿命的预测结果

3.1 Larson-Miller参数法预测剩余寿命

图1为运行后材料在不同温度下的持久强度试验数据。图2是利用原材料持久强度的统计数据与图1数据统计计算得出的Larson-Miller参数曲线。可见，运行15万h后，主蒸汽管道弯头材料的持久强度与原材料相比有明显的降低。

设定该主蒸汽管道的运行温度为550℃保持不变，将上述根据持久试验结果回归得到的Larson-Miller参数方程代入方程组（1），计算得出主蒸汽管道乙侧第一个弯管的剩余寿命为73 515h，等效运行应力为103.97MPa。该等效运行应力高于用有限元方法在稳态运行工况条件下计算得出的最大应力，说明在已知运行时间内被评估材料所承受的当量应力比稳态运行参数条件下计算出的应力要高，因此仅用稳态运行工况参数来计算材料的剩余寿命是不准确的。

3.2 高温蠕变裂纹开裂与扩展寿命法预测剩余寿命

试验时试样所加载荷根据式（5）进行计算：

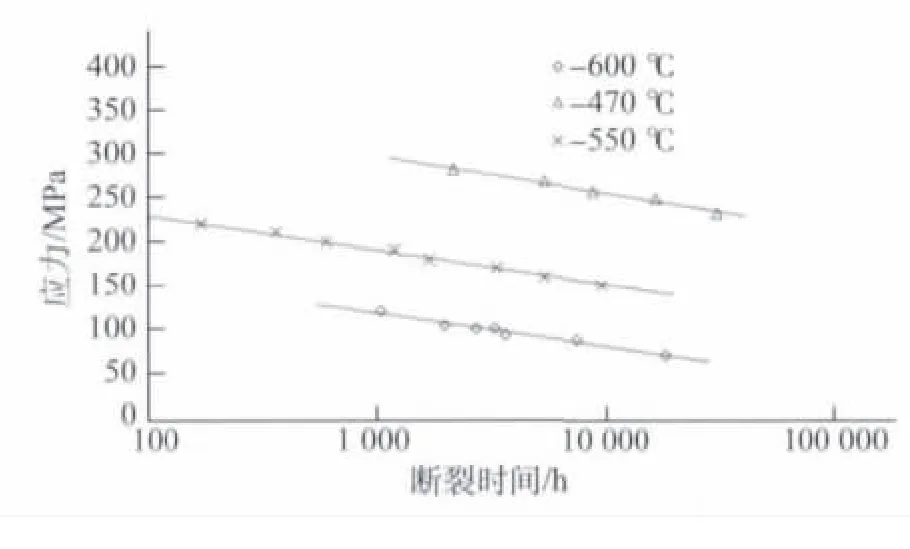
图1 取样弯管试样在不同温度下的持久性能Fig.1 Creep-rupture properties of sampling bend at different temperature

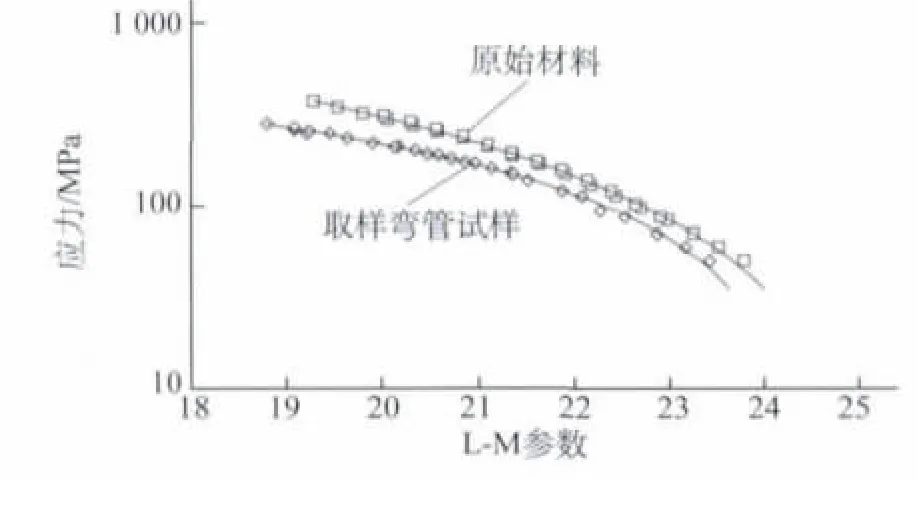
图2 取样弯管试样和原始材料持久剩余寿命评估的L-M曲线Fig.2 Larson-Miller curves of residual life assessment for sampling bend and original material

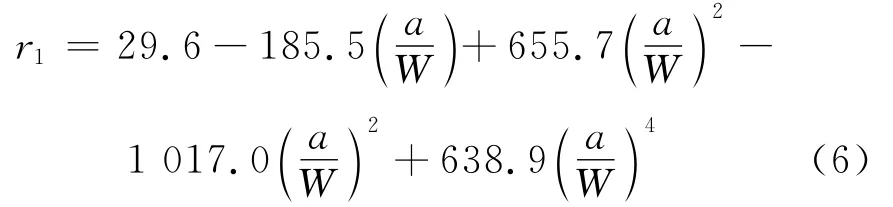
式中：P为加载载荷；B为试样厚度；W为试样宽

度；r1为几何形状系数；a为预制裂纹长度。

根据图3可以得到主蒸汽管取样弯管初始载荷KI与高温蠕变裂纹开裂时间以及裂纹扩展速率之间的关系，分别见图4和图5。

从图4可以看出，在550℃下，高温蠕变裂纹开裂试验时的初始加载载荷KI与裂纹开裂时间在双对数坐标上具有良好的线性关系，因此可以根据回归方程计算出式（2）中的各项参数。根据等效运行应力计算出相对应的初始载荷KI，进一步计算出取样弯管的开裂时间为116 571h。

从图5可以看出，裂纹扩展速率与裂纹尖端的应力场强度因子在双对数坐标上也具有良好的线性关系，并能回归计算出式（3）中的B1、n参数，再根据测得的取样弯管在各试验条件下的蠕变断裂韧度δcc，以及550℃下的高温屈服强度和弹性模量，计算出临界裂纹长度。根据式（3）计算出主蒸汽管道取样弯头蠕变裂纹的扩展时间为36 783h。

图3 在550℃和不同初始载荷下紧凑拉伸试样两端电位随时间变化的曲线Fig.3 Potential at each ends of compact tension sample vs time at 550 ℃ and different initial loads

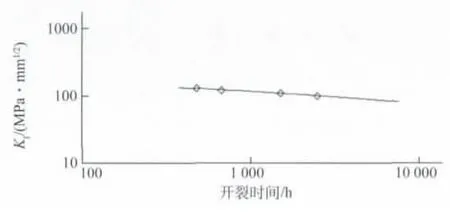
图4 取样弯管在550℃下的初始载荷KI与裂纹开裂时间之间的关系Fig.4 Initial load vs crack initiation time for sampling bend at 550℃

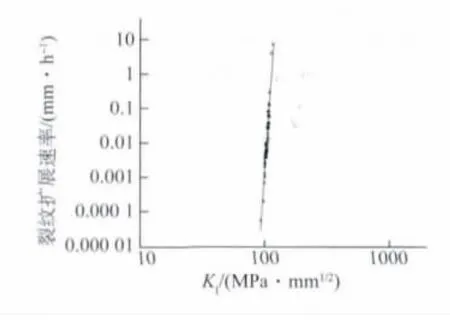
图5 取样弯管在550℃下的加载载荷KI与裂纹扩展速率之间的关系Fig.5 Crack growth rate vs initial load KI for sampling bend at 550℃

高温蠕变裂纹的开裂和扩展至临界裂纹长度的总时间为153 354h，该结果比Larson-Miller参数法评估得到的73 515h的剩余寿命长。另外，当蠕变裂纹形成后，裂纹的扩展时间比裂纹的开裂时间要短很多，因此一旦有蠕变裂纹形成，对于主蒸汽管道而言是极其危险的。在日本，是不允许设备带缺陷运行的［2］。

对比上述两种方法对主蒸汽管道弯管剩余寿命的评估结果可知，利用Larson-Miller参数得出的剩余寿命比高温蠕变裂纹开裂和扩展法得出的剩余寿命要短，这说明材料的持久寿命损耗相对比较严重，因此从电厂运行的安全性角度出发，该主蒸汽管道的剩余寿命应以Larson-Miller参数得出的剩余寿命73 515h为依据，按照机组年有效运行时间7～7.5万h计算，该机组主蒸汽管道还可安全运行约10a。

4 预测结果的试验验证

由于材料的性能取决于其组织，材料使用寿命的耗损是由材料组织老化引起的。因此，在对主蒸汽管道进行剩余寿命评估时，可以用显微组织的变化对上述剩余寿命评估结果进行验证。

由图（6）～（8）可见，与原始材料的显微组织相比较，主蒸汽管道取样弯管的显微组织有较大变化，虽然组织仍为回火索氏体，但马氏体位向已不明显；析出的碳化物弥散分布在原马氏体板条上，而且尺寸已经长大，并且在晶界上有链状碳化物析出，如图6和图7（c）所示。碳化物的链状分布会影响到材料的晶界结合强度，是材料老化过程中必然发生的结果。随着运行时间的延长，碳化物会进一步聚集、长大，并在晶界上产生蠕变孔洞，直到材料失效。而取样弯管的组织中未发现蠕变孔洞。

图6 取样弯管的OM形貌Fig.6 OMmorphology of sampling bend

图7 取样弯管的TEM形貌Fig.7 TEMmorphology of sampling bend：（a）carbides precipitated in transgranular of ferrite；（b）tempered sorbite；（c）carbides precipitated at grain boundary and（d）carbides precipitated in tempered sorbite

图8 晶内粒状M23C6型碳化物的形貌与衍射花样Fig.8 Bright field image（a），dark field image（b）and diffraction pattern（c）of granular M23C6carbon in transgranular

根据透射电镜的分析结果可知，取样弯管组织中的碳化物仍以M23C6型碳化物为主并出现球化，亚晶界上的碳化物形态明显拉长，晶内碳化物相对细小。

该主蒸汽管道取样弯管组织的特征表明该弯管还处于正常的蠕变第二阶段［19－21］，这就意味着材料的使用寿命还远未达到完全耗损的程度，验证了上述剩余寿命的评估结果正确。

5 结 论

（1）在运行后取样弯管持久性能试验的基础上，并应用积累的高温持久性能统计数据建立了弯管的Larson-Miller参数方程，统计估算出运行15万h后主蒸汽管道的剩余寿命为73 515h，等效运行应力为103.97MPa。

（2）在对运行后取样弯管的高温蠕变裂纹开裂和扩展速率试验的基础上，并应用蠕变裂纹开裂和扩展寿命评估法，估算出已运行15万h的主蒸汽管道在等效运行应力条件下的剩余寿命为153 354h。

（3）主蒸汽管道取样弯管组织和碳化物的分析结果表明其还处于正常的蠕变第二阶段。

（4）根据上述预测结果，该主蒸汽管道弯管在当前工况条件下仍可正常运行近10a，此结果得到了显微组织的验证。

［1］李耀君，任爱.火电厂重要部件的寿命管理［J］.热力发电，1999（4）：42-46.

［2］田文莉.火力发电设备剩余寿命评价技术［J］.电力情报，1994（1）：97-102.

［3］VISWANATHAN R.Damage mechanisms and life assessment of high temperature components［M］.Ohio：ASMInternational，1989：59-103.

［4］STOPPATO A，BENATO A，MIRANDOLA A.Assessment of stresses and residual life of plant components in view of lifetime extension of power plants［C］//Proceedings of ECOS 2012-the 25th International Conference on Efficiency，Cost，Optimization，Simulation and Environmental Impact of Energy Systems.Perugia：［s.n］，2012.

［5］European creep collaborative committee（ECCC）.Residual lifeassessment and microstructure［R］.［S.l.］：［s.n］，2005.

［6］宋志坤，刘伟，何庆复.金属材料热疲劳寿命的定量研究方法［J］.机械工程材料，1999，23（5）：4-5.

［7］蔡庆木，刘月明，黄昌清，等.火电厂高温压力管道寿命预测模型的可靠性及进展［J］.机械工程材料，2012，36（12）：5-9.

［8］潘文越，高向东，凌祥.高温炉管剩余寿命评价技术最新进展［J］.江苏化工，1997，25（1）：14-16.

［9］崔朝英，乔学亮.火电厂主蒸汽管道寿命评估方法［J］.华北电力技术，2002（11）：51-54.

［10］NONAKA I.Residual life evaluation and repair procedures for high temperature boiler piping［J］.OMMI，2003，2（1）：1-14.

［11］莫剑.压力容器及管道剩余寿命的评估方法［J］.化工装备技术，2004，25（5）：32-34.

［12］杨王玥，李志文.θ法预测12Cr1MoV钢主蒸汽管道材料剩余寿命［J］.金属学报，1999，35（7）：721-725.

［13］高锋，刘晖，樊玉光，等.蒸汽管道剩余寿命评估方法评述［J］.腐蚀与防护，2008，29（5）：295-297.

［14］郑晓红，赵翔，曹欣玉，等.锅炉高温承压部件剩余寿命的评估及应用［J］.锅炉技术，2003，34（4）：24-29.

［15］束国刚，李益民，梁昌乾，等.10CrMo910钢薄壁主蒸汽管道θ法寿命评估及其应用研究［J］.热力发电，2000（4）：36-41.

［16］陈国宏.由内壁氧化层厚度测评过热器管道的剩余寿命［J］.河南科技大学学报，2004，25（6）：24-27.

［17］李耀君，任爱.应用老化因子方法评估高温部件的状态和寿命［J］.热力发电，2002（3）：46-48.

［18］姜鹏，徐鸿，韩静茹.基于概率理论的主蒸汽管道寿命可靠性评估［J］.现代电力，2008，25（5）：35-39.

［19］HU Zheng-fei.Heat-resistant steels，microstructure evolution and life assessment in power plants［M］//Thermal Power Plants.［2013-05-20］.http：//www.intechopen.com/books/thermal-power-plants/heat-resistant-steels-microstructure-evolution-and-life-assessment-in-power-plants.

［20］张军，王志武，原素芳，等.高井电厂1号炉主蒸汽管直管段剩余寿命评估［J］.黑龙江电力，2004，26（5）：389-394.

［21］DOBRZANSKI J.The classification method and the technical condition evaluation of the critical elements′material of power boilers in creep service made from the 12Cr-1Mo-V［C］//13thInternation Scientific Conference on Achievements in Mechanical and Materials Engineering.Poland：AMME，2005：107-112.