基于EEMD-NExT的低频振荡主导模式工况在线辨识与预警

汪颂军，刘涤尘，廖清芬，周雨田，王亚俊，王乙斐，赵一婕

（武汉大学 电气工程学院，湖北 武汉 430072）

0 引言

随着全国联网程度的不断加深，低频振荡日益成为危及电网安全稳定运行的突出问题之一。基于系统日常运行工况下的实测轨迹进行的低频振荡模式在线辨识，对于低频振荡的在线监测、预警、控制器设计、系统阻尼优化等具有重要意义[1-3]。

目前对电力系统低频振荡进行分析一般基于系统扰动后的响应轨迹，常用的方法有傅里叶变换、ARMA算法、Prony分析、小波算法、希尔伯特-黄变换（HHT）、旋转不变技术（ESPRIT）等[4-6]，已有研究证明这些方法均能较准确地辨识出系统的模式信息。但是这类辨识方法均需对系统施加激励，只能在系统发生振荡后辨识出当时的系统特性，作出告警，并不能给出系统正常运行状态下的模式信息，也无法实现“全天候”监控和真正意义上的预警[7-8]。近年来基于环境激励的模式辨识研究已在桥梁、建筑、汽轮机、飞机等[9]领域展开，电力领域也逐步开展了一些研究：文献[10]探讨了工况模式分析在低频振荡辨识中的应用，论述了电力系统低频振荡和一般振动力学数学模型的相似性；文献[7]通过系统建模证明了负荷波动作为激励信号的可行性，以上研究为工况模式分析在电力系统的应用做好了铺垫。自然激励技术 NExT（Natural Excitation Technique）[9，11-12]是工况模式分析的有效方法，它可以避免传统模式辨识人工激励给电力系统带来的伤害，实现系统在工况下的在线模式识别，其在电力领域仅在文献[13]中有应用，值得更进一步的研究。

集合经验模式分解EEMD（Ensemble Empirical Mode Decomposition）[14-15]是经验模式分解 EMD（Empirical Mode Decomposition）的发展，既继承了EMD的优点，同时通过向原始信号添加白噪声改善了模式混叠问题。它是一种自适应的分析方法，适合处理工程中的非线性、非平稳信号。

基于此，本文将NExT与EEMD结合，提出一种适合于工况下的低频振荡主导模式辨识方法。首先通过EEMD将工况下的实测时变信号分解为若干个单自由度的本征模式，凭借EEMD时空滤波器、互相关系数和能量权重比筛选出真实主导模式分量，然后通过NExT求互相关函数以代替传统的脉冲响应，至此就实现了工况下把非平稳的多自由度系统的模式辨识问题转化为单自由度系统的脉冲响应辨识问题，最后对互相关函数分别通过Teager能量算子TEO（Teager Energy Operator）求出模式幅值和频率、能量分析求阻尼比、峰值法求相位。

1 EEMD

1.1 EEMD原理

为了改善EMD出现的模式混叠现象，Wu Zhaohua等提出了EEMD方法，其本质是一种叠加高斯白噪声的多次EMD。下面介绍EEMD的步骤。

a.产生N条随机正态分布的白噪声ni（t）分别加入到原始信号 x（t）中，得每次加噪后的信号 xi（t）为：

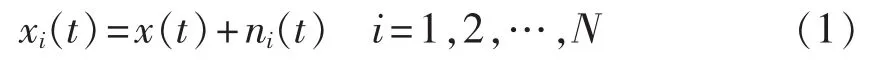
b.对每条加噪后的信号 xi（t）进行 EMD，得：

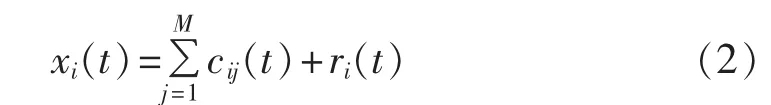
其中，cij（t）为第i次加入高斯白噪声后分解得到的第 j个本征模式函数（IMF）分量；ri（t）为对 xi（t）进行EMD后的余项。

c.将N组分解结果中对应的IMF分量求均值，则：

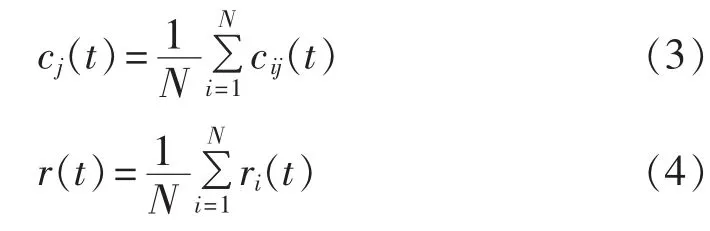
其中，cj（t）为对原始信号进行EEMD得到的第 j个IMF 分量；r（t）为余项。

EEMD算法流程如图1所示。

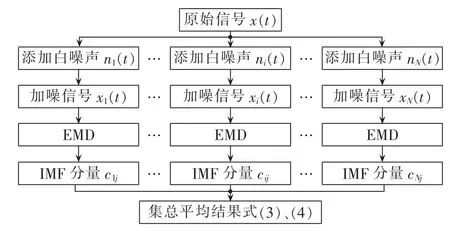
图1 EEMD算法流程图Fig.1 Flowchart of EEMD algorithm

1.2 EEMD时空滤波器

EEMD得到的IMF分量频率由大到小，利用这点本文基于EEMD构造时空滤波器组（TFB），其滤波信号为：

其中，xˆ（t）为滤波器输出信号；l，hє[1，M]。

当l=1且h＜M时，TFB为高通滤波器；当 l＞1且h=M 时，TFB为低通滤波器；当 1＜l≤h＜M时，TFB为带通滤波器。

1.3 互相关系数

原始信号经EEMD所得的IMF分量中常包含一些虚假分量，而这些虚假分量与原始信号无关且不能反映原始信号的特征，因此有必要将其辨别出来并予以剔除。基于互相关系数来判断IMF分量的真伪是一种行之有效的方法，通过求取分解后的各IMF分量与原始信号的互相关系数，假定互相关系数很小的对应IMF分量为伪分量。设2个时间序列 x（n）、y（n），它们的互相关系数 ρxy的表达式如式（6）所示。

互相关系数只是一个比率，不是等单位量度，互相关系数的正负号只表示相关的方向，绝对值表示相关的程度。

1.4 信号能量权重

电力系统低频振荡大多是多个模式的组合，其中阻尼比小且振荡幅度大的主导模式特征信息是电力工作者最为关心的。当信噪比足够大时以信号能量作为定性分析指标，从EEMD结果中经过滤波去伪后提取真实模式中能量权重最大的一个IMF分量作为主导模式加以分析。

信号x的能量表达式为：

其中，t0、t1分别为仿真开始和结束的时刻。

信号能量权重比定义为：

其中，Ef（i）为真实模式中第 i个 IMF 分量的能量；m为真实模式IMF分量的总个数。

2 NExT

NExT是由JAMES等提出的一种适合于环境激励的时域模式参数辨识方法，它的基本思想为：线性系统在白噪声环境激励下，结构中2点之间响应的互相关函数和脉冲响应函数有相似的表达式，求得互相关函数之后就可以运用时域模式辨识方法对其进行辨识。

对于自由度为Q的线性系统，于系统k点处加激励 fk（t），则系统 i点的响应 xik（t）为：

其中，φir为第i测点的第r阶模式振型；akr为仅与激励点k和模式阶次r有关的常数项；λr为系统的第r阶特征值。

根据振动模式理论，当系统的k点受到单位脉冲激励时，则系统i点的脉冲响应函数hik（t）为：

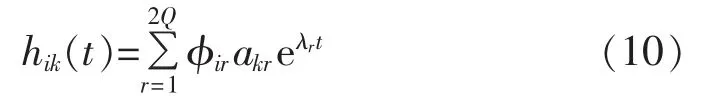
当系统k点处受到激励fk（t）时，系统i点和j点的响应 xik（t）和 xjk（t）的互相关函数为：

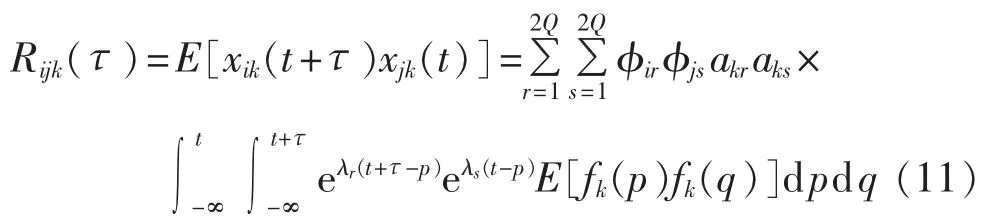
其中，E[·]表示求期望。

假定激励f（t）是理想白噪声，根据相关函数的定义，则有：

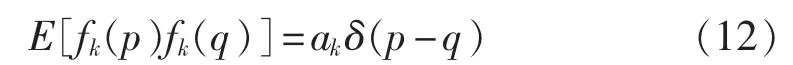
其中，δ为单位脉冲激励；ak为仅与激励点k有关的常数项。

将式（12）代入式（11）并积分，得：

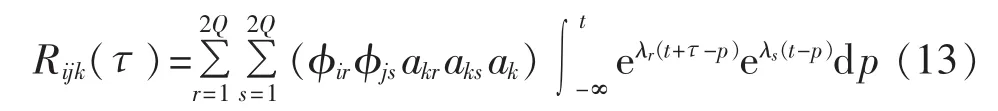
对式（13）的积分部分进行计算并化简，得：

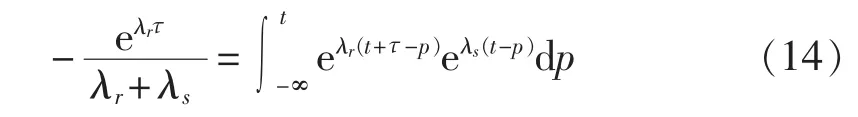
将式（14）代入式（13），得：

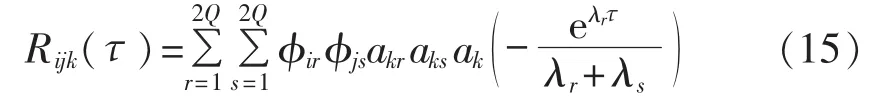
对式（15）做进一步的化简，经整理得：

其中，bjr为仅与参考点j和模式阶次r有关的常数项。

对比式（16）和式（10），可以发现两者的数学表达式在形式上是完全一致的，因此互相关函数具有和系统的脉冲响应函数同样的性质，可与其他模式辨识方法结合起来进行环境激励下的模式识别。

3 低频振荡主导模式识别

3.1 模式识别

3.1.1 Teager能量算子

Teager能量算子[16-18]具有健壮性和快速响应能力，能迅速跟踪信号的幅值和频率。

设幅值和频率均时变的工程信号为：

由文献[17]可知信号xn的瞬时数字角频率、实际频率、幅值分别为：

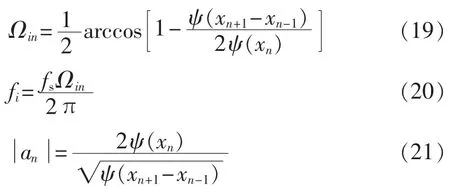
EEMD得到的IMF分量频率变化非常小，由于边际效应两端数据存在误差，计算过程中取合适的中间段数据求均值。

3.1.2 能量分析法

信号能量分析法[19]的原理是基于阻尼耗散能量思想，可将阻尼特性从用半周期能量描述的物理过程中提取出来。

振荡信号x（t）的半周期能量定义为：

其中，ti为某一过零点时刻；Td为振荡周期。

文献[19]已给出信号 x（t）的阻尼比 ξ为：

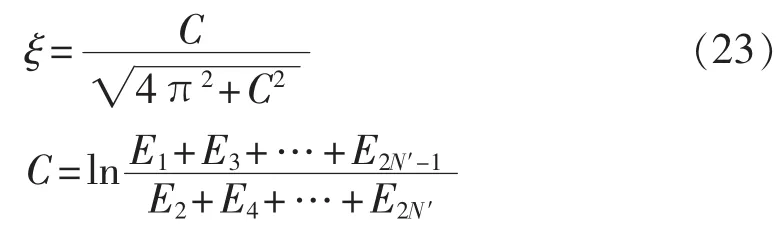
3.1.3 峰值法

由文献[20]可知，已知频率f和阻尼比ξ后，相位θ为：

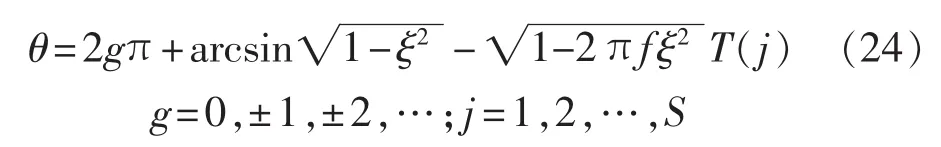
其中，T（j）为信号的最大正峰值时间；S为最大正峰值个数；-π≤θ≤π。

将 j=1，2，…，S 代入式（24），可得：

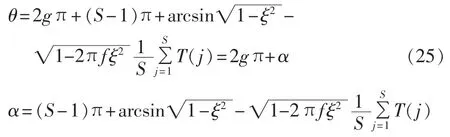
由于-π≤θ≤π，可得：

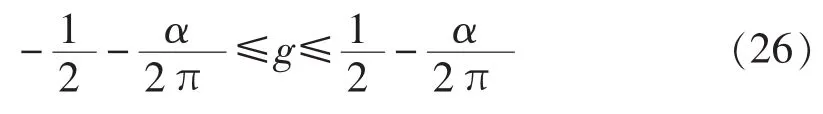
由于g取整数，故可由式（26）确定g值，然后根据式（25）得到相位角。

3.2 基于EEMD-NExT的主导模式识别与预警

基于EEMD-NExT的低频振荡主导模式工况在线辨识与预警流程如图2所示，具体步骤如下：

a.通过WAMS平台获取系统正常运行下的2个信号并对其进行预处理，然后分别作EEMD；

b.对EEMD得到的IMF分量由EEMD滤波器设置阈值获取低频振荡范围内的分量；

c.利用互相关系数识别所得分量的真假，将虚假模式予以剔除，得到真实模式；

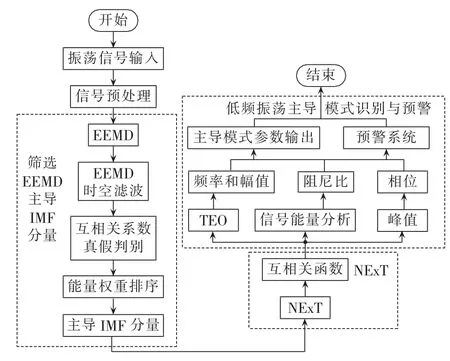
图2 基于EEMD-NExT的低频振荡主导模式辨识与预警Fig.2 Identification and warning of low-frequency oscillation dominant mode based on EEMD-NExT

d.借助能量权重比对所得的真实模式分量进行排序，选择能量权重比最大的分量作为主导模式分量；

e.通过NExT对2个主导模式分量求互相关函数，将其作为主导模式辨识的信号；

f.对所得互相关函数分别通过Teager能量算子求时变幅值、时变频率，通过能量分析求取阻尼比，时域峰值法求相位；

g.比较主导模式阻尼比与预警阈值大小，判断系统是否发出告警。

4 算例仿真

4.1 数值信号算例

取复合数值信号

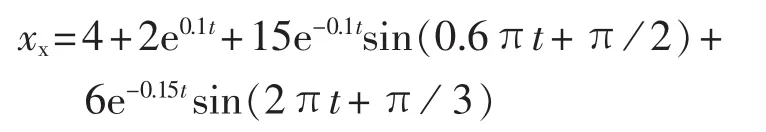
验证EEMD的抗模式混叠效果，以及依据相关系数甄别虚假模式的有效性和本文模式识别方法的可行性。

信号xx的EEMD结果如图3所示。设定EEMD时空滤波器的阈值，此处设置带通滤波频率范围为0.1～2 Hz，得到 imf7、imf8、imf9、imf10 这 4 个 IMF 分量，求取它们与原信号xx的相关系数如表1所示，并根据本文模式识别方法辨识各分量的模式特征，结果如表2所示。

由表1可知，imf7和imf10的互相关系数均小于0.4；imf8和imf9的互相关系数分别为0.6469、0.9152，均比较大。由此判定imf7和imf10分量为伪分量。比较表2中imf7、imf8的模式信息和表3模式2的理论值可知，尽管两者频率很接近，但imf8的其他模式信息更接近理论值，由此进一步验证了imf 7为虚假模式；表2中imf10的频率为0.1638Hz，真实模式中并不存在该分量，可见根据互相关系数判断imf10为虚假分量是有效的。表3为2个真实模式的理论值和本文方法的辨识结果，本文方法辨识误差较小，是一种低频振荡模式辨识的有效方法。

4.2 EPRI-36节点算例

本文选取电科院的EPRI-36节点系统作为仿真算例，验证本文方法在多机系统研究中的有效性。

为了比较真实地模拟系统工况运行的特点，本文选择负荷随机扰动作为环境激励，分别在负荷9、19和20上设置幅度为0.2 p.u.的功率随机波动。文献[21]表明通过等值单机曲线可以很好地提取出主导振荡信息，为此根据扩展等面积准则（EEAC）理论对系统进行分群得，机组 1、2、3、4、5、7、8 为 S 群，机组6为A群，分别求取S群和A群的惯量中心δS、δA，并对它们添加λSNR=20 dB的高斯白噪声以尽可能地再现工程实际中信号受噪声干扰的特点。分别对加了高斯白噪声的 δS和 δA进行 EEMD，此处限于篇幅仅给出δS的EEMD效果图，如图4所示。

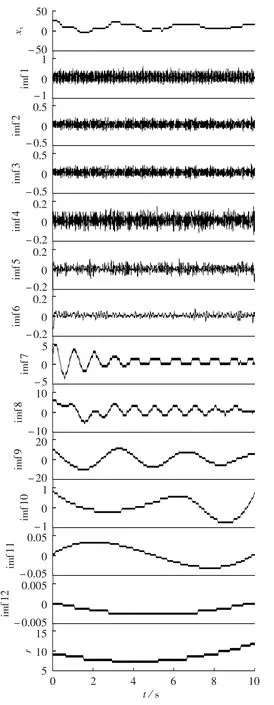
图3 xx及EEMD效果图Fig.3 xxand its EEMD results

表1 EEMD时空滤波后的IMF分量互相关系数Table 1 Cross-correlation coefficient of IMF components after EEMD spatiotemporal filtering

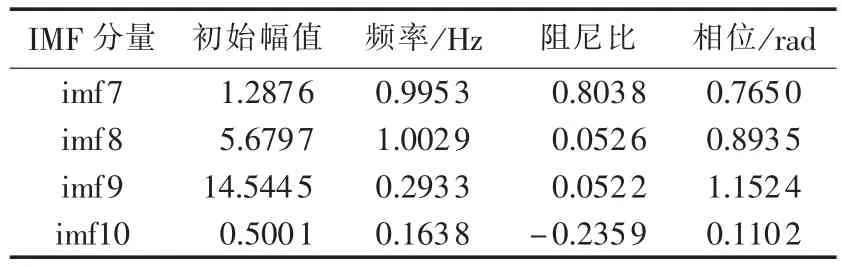
表2 EEMD时空滤波后的IMF分量模式信息Table 2 Mode information of IMF components after EEMD spatiotemporal filtering

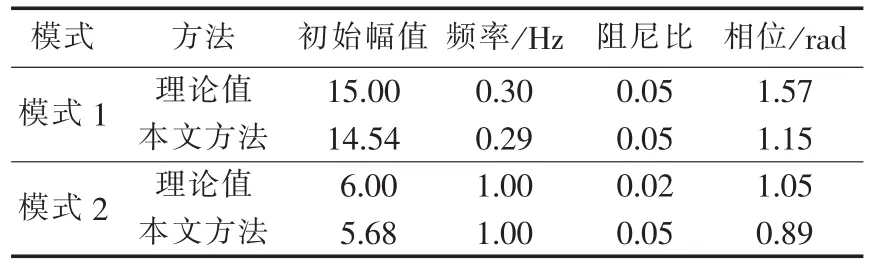
表3 本文方法辨识结果与理论值比较Table 3 Comparison between results identified by proposed method and theoretical values

图4 δS的 EEMD 效果图Fig.4 δSand its EEMD results

区间振荡模式较本地振荡模式危害更大，其频率范围为0.1～1Hz，将该范围留足裕度后设置为EEMD时空滤波器的带通范围，求取滤波后的各IMF分量的互相关系数见表4。对imf6、imf7求取信号能量后，并计算其能量权重比从而可得能量权重排序，结果如表4所示，可知imf6为主导模式。

取δS和δA中对应的主导模式通过NExT求取互相关函数如图5所示，再对其通过Teager能量算子求取主导模式频率，通过能量分析求阻尼比。表5列出了本文方法、EMD-TEO-能量分析算法[18]、Prony 算法、小干扰分析主导模式辨识结果，其中EMD-TEO-能量分析算法和Prony算法的辨识结果均为对发电机7与发电机1的相对功角信号加噪20 dB后辨识所得，采样频率均为100 Hz。

表4 EEMD时空滤波后的IMF分量互相关系数Table 4 Cross-correlation coefficient of IMF components after EEMD spatiotemporal filtering

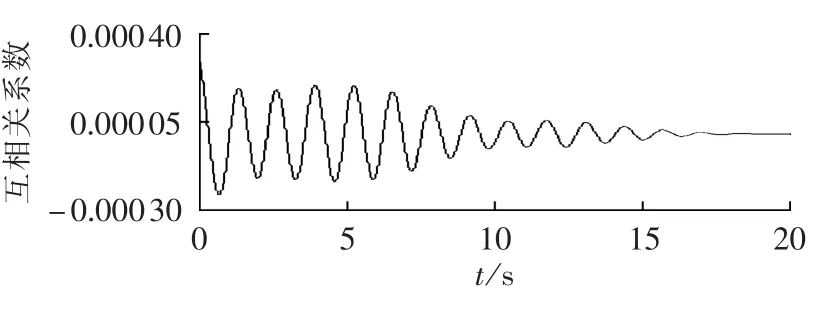
图5 NExT法得到的互相关函数Fig.5 Cross-correlation function by NExT method

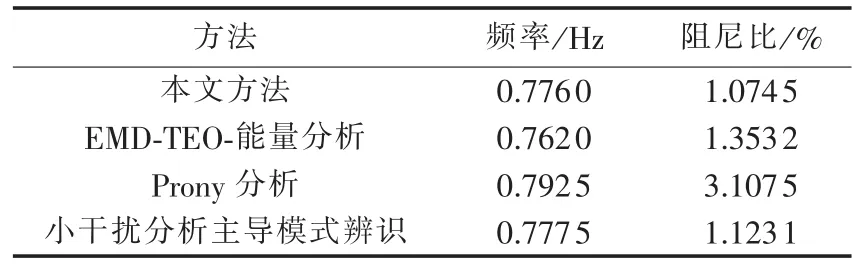
表5 4种方法对含噪信号辨识结果对比Table 5 Comparison of identification results among four methods for signal with noise

由表5可知，当噪声为20 dB时，4种方法均能辨识出EPRI-36节点系统的主导模式，本文方法和EMD-TEO-能量分析的辨识结果精度均高于传统的Prony算法。本文方法的辨识结果更接近理论值，具有良好的抗噪性能，相比其他辨识方法无需人工激励，是一种能有效在线辨识工况模式的方法。一般认为，机电振荡模式的阻尼比小于0.03时系统会发生低频振荡失稳，故本文设置预警阈值为0.03，由辨识得到的主导模式阻尼比在阈值以下，此时系统发出告警须采取有效控制措施。

5 结论

a.EEMD与傅里叶变换、Prony分析等传统辨识方法相比，更适合处理实际工程中的非线性、非平稳工况信号，无需考虑定阶问题，同时抗噪能力强且能改善模式混叠现象。

b.通过EEMD时空滤波器对IMF分量滤波可以得到低频振荡工作范围内的信号，互相关系数能将虚假模式从真实模式中辨识出来并将其从中剔除，能量权重排序能找出主导模式分量。

c.本文采用了NExT，它是环境激励模式识别的有效方法，避免了传统模式辨识方法需人工激励给电力系统安全带来的危害，辨识出的模式参数更符合实际情况。

d.本文方法可以实时快速地跟踪提取系统的主导模式信息，因此其在基于WAMS实测数据的低频振荡分析、在线监测、预警及阻尼控制器设计等方面具有较好的实际应用价值。