基于局部区域梯度最小点的遥感图像镶嵌算法

程 红，郑 悦，孙文邦

(中国人民解放军空军航空大学，长春 130022)

0 引言

遥感图像镶嵌的目的是构造一个视觉效果好的整幅图像，以便更好地进行处理、解译和分析。在镶嵌图像中的拼接缝附近，2景图像在色调或纹理上的差别都会产生明显的拼接缝痕迹。由于地面环境的微小变化、成像角度、曝光强度和自然光线照射强度等的差异等都可能造成镶嵌边界附近色调和纹理上的差异。因此，在遥感图像镶嵌过程中，寻找一条最佳拼接缝并对其进行消除有着重要意义。

目前，常用的拼接缝消除方法有平分线法和灰度差值最小法。平分线法是将相邻2景图像重叠区域的平分线作为拼接缝进行图像镶嵌，操作简单，易于实现，但其确定的拼接缝上的对应像素的灰度差异往往很大，且易穿越重要目标;因此，拼接缝消除后有可能使得重要目标产生较大变化，影响后期的图像解译。灰度差值最小法则是在2景图像重叠区域内选取对应灰度差值最小的像素作为最佳拼接点，再将最佳拼接点连接起来，形成最佳拼接缝。使用该算法进行图像镶嵌，当最佳拼接缝上2幅图像灰度差别很小时，镶嵌的图像不存在明显的拼接缝;但当重叠区域中图像的灰度差异较大时，该方法难以在重叠区域中找到满意的拼接缝;对于内容复杂的图像，当所选拼接缝与某些地物边缘相交时，有可能在后期消除拼接缝时出现消除效果不理想、甚至产生局部突变的现象[1－2]。在目前寻找最佳拼接缝算法的研究中，自Duplaquet采用动态规划的思想确定最佳拼接缝以来，方亚玲等[3]又在其基础上进行了改进，但仍未解决动态规划法容易陷入局部最优解的问题;Wen，Chon 和王军等[4－6]分别利用灰色理论和最大相关系数寻找最佳拼接缝;方贤勇[7]通过带权有向图的最佳切割路径来确定最佳拼接缝;Pan等[8]利用 Voronoi图法(又称泰森多边形或Dirichlet图，是由连接2邻点直线的垂直平分线组成的连续多边形)有效地解决了寻找多幅图像最佳拼接缝的问题，但对于初始拼接缝的修改仍有待改进;范永弘等[9]采用蚁群优化算法确定数字表面模型权值，然后基于流水模型设计了拼接缝自动选择规则，最后利用数学形态学运算对所提取的拼接缝进行膨胀处理，有效规避建筑物的投影差，避免拼接缝与建筑物边缘重合，确保了最佳拼接缝提取的有效性。上述方法大多只考虑到对应像素灰度的差异最小，却没有考虑图像中目标的完整性;因而确定的最佳拼接缝会穿越图像中的目标，从而破坏了目标的完整性，影响到整幅镶嵌图像的质量。针对以上问题，本文提出一种能够有效避免切割图像中的目标，尽量使得找到的最佳拼接缝既能绕过目标边缘、又保留目标完整性的最佳拼接缝寻找方法。实验结果表明，该方法具有一定的可行性和有效性。

1 基本原理与算法流程

遥感图像灰度的梯度可以用来表示图像中灰度变化的快慢，梯度值愈大，说明该区域灰度变化愈剧烈(梯度值大的像素一般为图像中的边缘信息);梯度值愈小，则说明该区域灰度变化愈平缓，与周围像素的灰度值愈相近。因此，本文提出的最佳拼接缝寻找算法的基本原理是:通过计算重叠区域内各个像素灰度的梯度值，选取搜索范围内梯度值最小的像素(即灰度变化较为平缓的位置)作为最佳拼接缝，由此得到的拼接缝两侧图像灰度差异较小，可在一定程度上满足对应像素灰度差异尽量小的要求;并利于后期拼接缝消除处理，避免因拼接缝两侧灰度差异过大而导致的横向带状效应，最终提高图像的整体视觉效果。本文算法的技术流程如图1所示。

图1 本文算法的技术流程Fig.1 Technique flowchart of algorithm proposed in this paper

1)计算重叠区域内每个像素的灰度梯度值。图像f(x，y)在位置(x，y)处的梯度定义为

式中Gx和Gy分别为像素(x，y)在x方向和y方向的梯度。梯度向量的方向为(x，y)处f(x，y)的最大变化方向，其值为

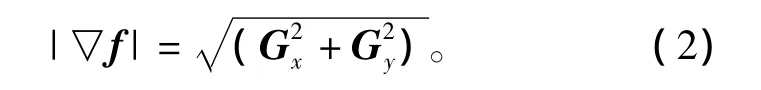
计算重叠区域内每个像素周围邻域(本文选取以当前像素为中心的3像素×3像素的邻域)内的“梯度和”;在起始行选择梯度和最小的点作为拼接缝的起始位置，为了使得最佳拼接缝处于图像重叠区域的中间区域(而不明显偏向于重叠区域的某一边界)，当出现梯度和相等的点时，选择距离重叠区域中垂线较近的点作为初始拼接点。

2)以确定的拼接缝初始位置为起点，以后每一行都在上一行已经确定的拼接缝位置所在列H(i－1)两侧各q个像素内(根据需要确定q，本文取q=5)寻找梯度和最小的点，作为该行的拼接缝位置;若出现2个点的梯度和相等的情况，由于每一行都是在以上一行拼接点为中心的两侧固定范围内寻找该行的最佳拼接点，所以拼接点的位置不会过多地偏离重叠区域的中间区域。因此，为了满足最佳拼接缝上对应像素差异最小的要求，尽量选择对应像素灰度差值较小的点作为该行的最佳拼接缝位置，该位置所对应的列值为H(i)。

3)连接各行确定的拼接点，即可在图像上得到最佳拼接缝的位置;再根据得到的位置对拼接缝进行消除。目前普遍采用的拼接缝消除方法是“渐入渐出法”和“强制改正法”。前者必须同时拥有2景具有重叠区域的待镶嵌图像，且在灰度差较大情况下易出现“鬼影”现象;后者只需要1景已经完成几何镶嵌的遥感图像即可，但其在消除原拼接缝的同时又易出现列方向上的横向带状效应，会影响镶嵌图像的整体视觉效果。针对以上问题，本文对强制改正法进行改进，提出一种“差值拼接缝消除算法”。其基本思想是:分别统计各行拼接缝两侧相邻像素的灰度差值，并使灰度差值在改正范围内逐渐过渡，越靠近拼接缝位置改正值越大，改正范围边界处的改正值为0;为了消除上述带状效应，对各改正值进行卷积平滑处理，得到每个像素对应的新的改正值;再根据新得到的改正值对各像素进行改正，最终得到无拼接缝、视觉效果较好的镶嵌图像。

2 仿真实验与对比分析

为说明本文算法的可行性和有效性，笔者在Intel(R)Core(TM)2 Quad CPU Q9400 2.66 GHz、内存4 GB的计算机上，Matlab7.1的编程条件下进行实验。选取的2景待镶嵌实验图像为某机场的航空遥感图像(图2)。

图2 实验用航空遥感图像Fig.2 Airborne remote sensing images for experiment

鉴于目前普遍采用的确定拼接缝算法为平分线法和灰度差值最小法，本文重点与上述2种算法进行对比实验，以验证本文算法的可行性和有效性。

2.1 与平分线法比较

图3分别为根据平分线法和本文算法确定的最佳拼接缝位置。

图3 本文算法与平分线法确定的拼接缝对比Fig.3 Comparison between seam－lines determined with proposed algorithm and bisection algorithm

很明显，用平分线法确定的最佳拼接缝固定在图像的中间位置，未能有效地避开图像中的建筑物或其他重要目标，并切割了机场跑道的影像(图3(a));而用本文算法确定的最佳拼接缝则在一定程度上绕开了图像中的目标(图3(b))。以红色圆圈所示区域中的机场跑道为例，本文算法确定的最佳拼接缝与机场跑道平行，绕开了跑道的边缘。由于本实验图像中机场跑道横穿整个重叠区域，因此确定的拼接缝不可避免地要与跑道相交;但若目标较小，本文算法确定的最佳拼接缝则可很好地绕开目标，达到较好的效果。如在图3(b)黄色圆圈所示区域中，本文算法确定的拼接缝有效地沿着2种不同地物的分界线将2种地物分别划分在不同的图像上，避免了机械地切割某一地物目标，从而保证了地物目标的完整性。这在一定程度上也解决了图像中的微小错位问题，即消除了结构性拼接缝。

使用本文提出的差值拼接缝消除方法对图3中的2幅图像进行拼接缝消除处理，结果如图4所示。

图4 本文算法与平分线法的拼接缝消除结果对比Fig.4 Comparison between seam－line removal results of proposed algorithm and bisection algorithm

由图4可以看出，2种方法的结果图像均实现了拼接缝的平滑过渡。但由于用平分线法确定的拼接缝位于图像中部(如红色框所示)，而图像中部的机场跑道是图像解译的主要目标，所以用平分线法确定的拼接缝直接切割了图像的主体，经消除灰度差异后整体影像色调偏暗，对比度不强，不利于图像分析(图4(a));而用本文算法确定的拼接缝由于绕开了机场跑道的中间区域，保证了机场跑道的完整性，拼接缝消除后跑道的主体色调正常，对比度也优于平分线法，从而更有利于图像的分析和解译(图4(b))。同样，在与上述分析对应的黄色框中，本文算法的对比度也优于平分线法，视觉效果较好。

为定量地说明本文算法的有效性，采用空间频率活动性(spatial frequency activity，SFA)和结构对比度(structural contrast degree，SCD)等评价指标对用上述2种算法得到镶嵌图像进行对比分析[10]。

SFA体现边缘的粗糙程度，反映了拼接缝消除效果的优劣。SFA值越小说明活动性越弱，即拼接缝消除效果越好、越光滑。空间频率分为空间行频率fr和空间列频率fc，分别定义为

式中:M，N分别为图像的列、行数;i，j分别为图像的列、行坐标。

SFA定义为

SCD体现镶嵌处理后图像灰度的整体和谐性。以sn，tn分别表示2景图像的重叠区域，镶嵌完成后的对应区域为hn，则SCD定义为

基于上述分析，分别对2种算法的拼接缝消除效果进行了参数对比(表1)。

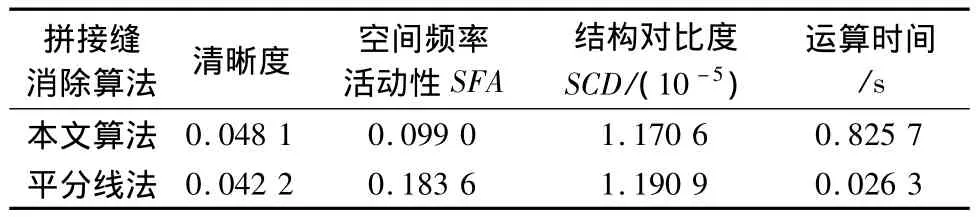
表1 本文算法与平分线法参数对比Tab.1 Comparison between parameters of proposed algorithm and bisection algorithm

从表1可以看出，用本文算法得到的镶嵌图像的清晰度较高;SFA和SCD均小于平分线法，即在镶嵌图像中拼接缝的消除使色调过度更平滑、灰度的整体和谐性更好。但在运算耗时方面，由于平分线法直接机械地以垂直平分线作为最佳拼接缝的位置，并未经过一定规则的筛选，因此平分线法的运行时间明显少于本文算法是符合实际情况的。但本文算法的运行时间已能够满足用户的需求。

2.2 与灰度差最小法比较

如图5所示，由于基于灰度值差最小方法确定的最佳拼接缝选取的是对应像素灰度差最小的点，因此在一定程度上也可以避开一些目标(如图5中黄色圆圈所示区域中的机场跑道);但其确定的拼接缝波动性较大，某些点与机场跑道相切或者过于接近，不利于后期的拼接缝消除。而用本文算法确定的拼接缝与机场跑道平行且相距一定距离，较稳定地沿绕着跑道的边缘。

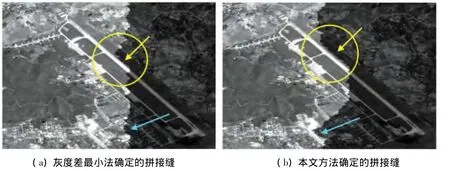
图5 本文算法与灰度差最小法确定的拼接缝对比Fig.5 Comparison between seam－lines determined with proposed algorithm and minimum gray difference algorithm

在图5的下部(如蓝色箭头所示)，用最小灰度 差法确定的拼接缝穿过了一些变化复杂的地物，若根据该方法确定的拼接缝进行拼接缝的消除，有可能会使同一地物出现不同变化，产生错误信息(图5(a));而用本文方法确定的最佳拼接缝则有效地绕过了变化复杂的地物，使拼接缝位于灰度变化较为平缓的区域，这样可以减少同一地物出现不同变化的现象，使得拼接缝消除处理后的镶嵌图像的整体视觉效果更佳(图5(b))。

分别对图5中2幅镶嵌图像采用本文提出的差值拼接缝消除方法进行拼接缝消除处理，得到结果图像如图6所示。

图6 本文算法与灰度差最小法的拼接缝消除结果对比Fig.6 Comparison between seam－line removal results of proposed algorithm and minimum gray difference algorithm

由图6可以看出，基于灰度差值最小的方法确定的拼接缝偏向图像的一边，因此容易造成拼接缝消除后的图像一边较亮而另一边较暗(图6(a))，图像的大部分偏亮，而较靠近右侧的图像偏暗，因此虽然消除了拼接缝痕迹，但由于灰度分布不均匀，仍然在一定程度上影响了镶嵌图像的整体视觉效果;而本文算法确定的拼接缝分布均匀，基本集中在图像中间区域，在消除灰度差异后，灰度分布较均匀，色调过渡自然(图6(b))，保证了图像中机场跑道主体部分的色调和对比度都比较适中，便于图像的分析处理。表2对比了2种拼接缝消除算法的参数。

表2 灰度差最小法与本文算法参数对比Tab.2 Comparison between parameters of proposed algorithm and minimum gray difference algorithm

由表2可以看出，与上一组对比实验相同，用本文算法得到的镶嵌图像的SFA和SCD均较小，即本文算法的拼接缝消除效果明显，色调过渡更为平滑，灰度的整体和谐性较高，图像较清晰，视觉效果基本令人满意;此外，本文算法的耗时少于灰度值差最小法，运算效率提高近30%，具有明显的优势。

3 结论

本文提出了一种利用图像灰度的梯度信息确定最佳拼接缝的算法，经过实验验证，具有一定的可行性和有效性。

1)本文在镶嵌图像的重叠区域内选取局部区域梯度最小点作为最佳拼接点，进而将最佳拼接点连接起来形成最佳拼接缝，根据确定的最佳拼接缝进行拼接缝消除的效果远好于目前常用的平分线法和灰度值差最小法。

2)本文提出的基于局部区域梯度最小点的最佳拼接缝寻找算法能够有效地绕开图像中目标的边缘，保留目标的完整性，使得拼接缝位于图像中灰度变化较平缓的区域;而本文提出的差值拼接缝消除方法能够在消除拼接缝的同时避免强制改正法容易产生的横向带状效应，尤其在镶嵌图像间灰度差异较大的情况下，这种优势更为明显。

3)通过清晰度、空间频率活动性(SFA)、结构对比度(SCD)和计算时间等参数的对比评价可知，使用本文方法得到的镶嵌遥感图像清晰，色调过渡平滑，具有较好的整体和谐性;且运算时间较少，效率明显提高。

[1]Davis J.Mosaics of scenes with moving objects[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition，Santa Barnara:IEEE，1998:354－360.

[2]温红艳，周建中.基于灰色理论的遥感图像最佳镶嵌线检测[J].计算机工程与应用，2009，45(15):31－33.Wen H Y，Zhou J Z.Optimal seam line detection algorithm of remote sensing image mosaic based on grey system theory[J].Computer Engineering and Applications，2009，45(15):31－33.

[3]方亚玲，焦伟利.利用对称动态轮廓模型自动检测最优镶嵌线[J].科学技术与工程，2007，7(14):3451－3456 Fang Y L，Jiao W L.Detecting the optimal seam line automatically in image mosaic with twin snakes model[J].Science Technology and Engineering，2007，7(14):3451－3456.

[4]Wen H Y，Zhou J Z.An improved algorithm for image mosaic[C]//International Symposium on Information Science and Engineering.Shanghai:ISISE，2008:497－500.

[5]Chon J，Kim H，Lin C S.Seam－line determination for image mosaicking:A technique minimizing the maximum local mismatch and the global cost[J].ISPRS Journal of Photogrammetry and Remote Sensing，2010，65(1):86－92.

[6]王 军，朱宝山，朱述龙，等.基于相关系数的遥感图像拼接线检测算法[J].测绘与空间地理信息，2011，34(3):151－153.Wang J，Zhu B S，Zhu S L，et al.A stitching line detection algorithm of remote sensing image based on correlation coefficient[J].Geomatics and Spatial Information Technology，2011，34(3):151－153.

[7]方贤勇.图像拼接技术研究[D].杭州:浙江大学，2005.Fang X Y.Studies on image mosaic[D].Hangzhou:Zhejiang University，2005.

[8]Pan J，Wang M，Li D R ，et al.Automatic generation of seamline network using area Voronoi diagrams with overlap[J].IEEE Transactions on Geoscience and Remote Sensing，2009，47(6):1737－1744.

[9]范永弘，万惠琼，靳建立，等.基于DSM的遥感图像拼接线自动生成技术[J].测绘科学技术学报，2011，28(1):33－36.Fan Y H，Wan H Q，Jin J L，et al.Remote sensing image mosaic line auto－ extraction based on DSM[J].Journal of Geomatics Science and Technology，2011，28(1):33－36.

[10]武 新，张焕龙，舒云星.基于视觉感知的镶嵌图像质量评价方法[J].计算机工程，2008，34(18):220－222.Wu X，Zhang H L，Shu Y X.Mosaic image quality evaluation method based on visual perception[J].Computer Engineering，2008，34(18):220－222.