一种基于MEMS传感器的无人飞艇航姿测量系统*

胡少兴， 刘东昌， 张爱武， 朱煜坤

(1.北京航空航天大学 机械工程及自动化学院，北京 100191；2.首都师范大学 三维信息获取与应用教育部重点实验室，北京 100037)

0 引 言

姿态信息是自动飞行控制系统最重要最基本的反馈信号。在无人飞艇上, 由于任务载荷有限, 高精度的大型测量设备将不能使用。微机电系统(micro-electro-mechanical system,MEMS)惯性传感器由于其质量、体积和功耗等方面的优势得到了广泛的应用。

针对多MEMS传感器姿态融合，国内外提出了许多先进的方法，如扩展卡尔曼滤波(EKF)方法，是一种递推滤波方法[1,2]，EKF方法广泛使用证明了它的正确性和有效性，但其是基于对非线性方程的线性化，当系统具有强非线性时线性化可能引起大的误差甚至造成滤波器的不稳定，并且EKF设计困难；比较常用的还有互补滤波法[3,4]，结合传感器频域的特点分辨和消除噪声，不需考虑信号的统计特性，但是文献中的方法是基于几何关系直接计算倾角，没有优化处理，容易造成姿态误差[5]。

针对现有算法存在的不足，本文提出了一种高效的姿态融合算法，充分利用重力场和地磁场特性，每次融合迭代过程只需根据辅助传感器计算出梯度，去修正陀螺仪数据给出最优估计。针对振动干扰问题提出新的思路，从传感器数据预处理和多传感器数据融合两方面双重抑制振动，取得了明显的效果。该算法采用了四元数表示方位，避免了欧拉角描述姿态时出现的奇异性问题。

1 无人飞艇航姿测量系统结构与工作原理

所描述的无人飞艇航姿系统主要由三轴陀螺仪、三轴加速度计、三轴磁力计以及ARM处理器组成，工作原理如图1所示，传感器数据经过预处理后经过专家系统的判断进行数据融合算法，最终输出艇体的姿态角—横滚角φ、俯仰角θ和航向角ψ。

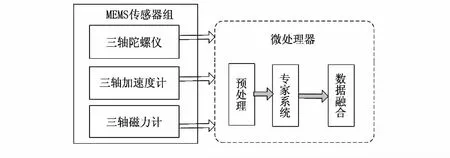
图1 系统总体结构图

2 传感器的数据预处理

机体振动对姿态的影响主要体现在其对加速度数据的影响。由于加速度计对振动极为敏感，当发动机(电机)运转时，尽管测量模块的周围会采取减震措施，但加速度的测量值中仍会有高频噪声，很不稳定，使得姿态输出会出现较大的误差。经实验和分析，振动情况下加速度计数据偏差主要是高频噪声，为此,设计了切比雪夫II型数字低通滤波器，对加速度的测量值进行低通滤波处理。

切比雪夫II型滤波器的特性是在通带内是单调的(在Ω=0附近最平坦)，在阻带内是等波纹的。滤波器的系统函数为

(1)

根据滤波要求的Ωc(截止频率)、N(迭代次数)和ε(波纹参数)，便可得到式(1)中的a和b值,继而得到差分方程

y(n)=b0x(n)+b1x(n-1)+…bN-1x(n-N+1)-

a1y(n-1)-a2y(n-2)-…aNy(n-N).

(2)

本节以采样频率为100 Hz，Ωc=12.5，ε=1，α=60为例，结合Matlab中的cheby2工具进行了契比雪夫II型滤波器设计，并针对加速度计数据进行了实验。

图2是加速度计Z轴数据在一定油门条件下的滤波前后对比效果图。

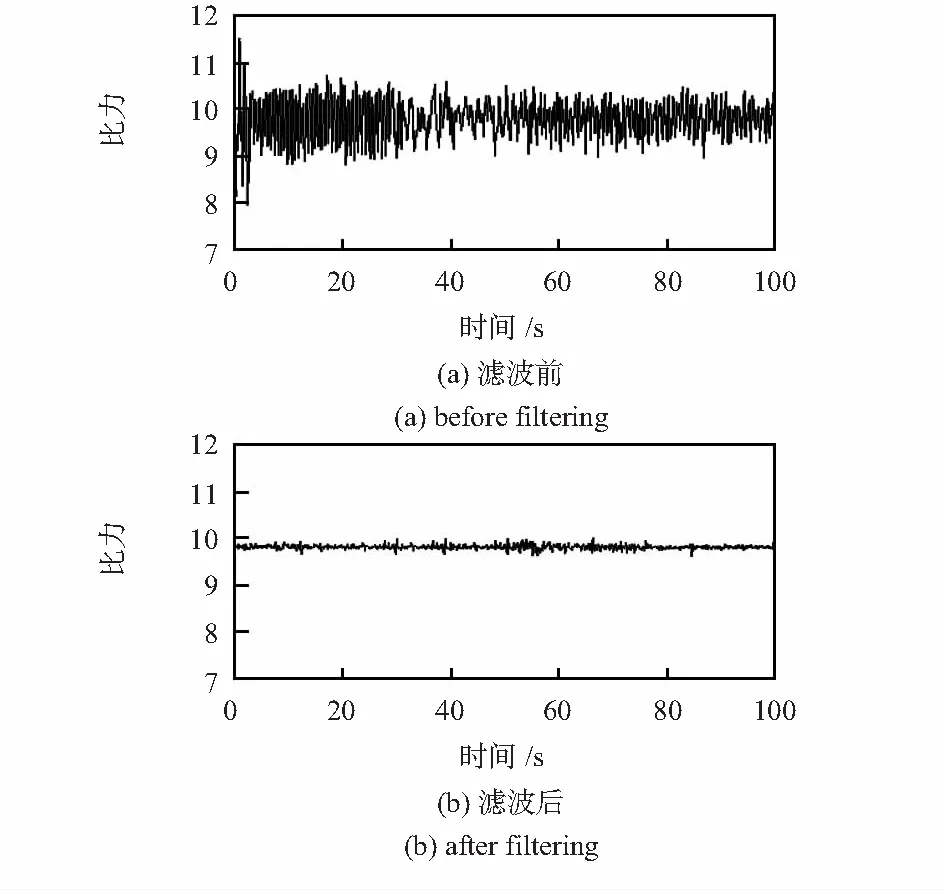
图2 有油门条件下加速度数据滤波前后效果图

由图2(a),(b)可以看出，经过切比雪夫滤波器后，加速度计的数据较为平整。由此可见，滤波处理能有效地减少艇体震动对加速度数据的影响。

3 姿态解算

进行姿态解算首先得定义坐标系，此处定义的导航坐标系，坐标轴Xe，Ye，Ze分别指向北、东和地；艇体坐标系中，X轴与艇身轴线平行，指向艇头；Z轴垂直于X轴指向艇身右侧；Y轴根据右手定则确定,如图3所示。

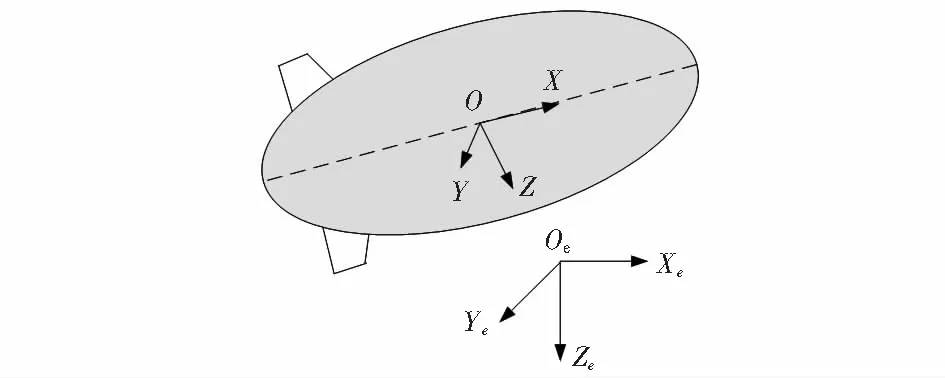
图3 坐标系定义

3.1 陀螺仪的姿态角初始估计

(3)

式中gx，gy，gz为陀螺仪实时的三轴角速率值。设采样间隔为Δt，则陀螺仪估计的四元数姿态值为

qgyr=qt-1+qtΔt.

(4)

3.2 基于最速下降法的姿态估计

作为辅助传感器，当艇体处于匀速或是静止时，加速度计和磁力计可以比较精确地估计姿态分量。根据重力和地磁场的特性，若规定重力方向为z轴正方向，则导航坐标系下重力加速度矢量，单位化后为G=[0，0，1]T；规定磁北方向为x轴正方向，单位化后H=[hx，0，hz]为导航坐标系下地磁常量，可以看出，这些分量中0和1的存在，在计算时可以极大提高解算效率，减轻计算负荷[7]。

这里定义误差函数

(5)

式中Ωqt为导航坐标系到艇体坐标系的四元数旋转矩阵

(6)

式中at=(ax,ay,az)为三轴加速度计测量的重力加速度矢量，mt=(mx,my,mz)为三轴磁力计测量的地磁场矢量。‖ΩqtG-at‖为艇体坐标系下重力加速度测量值与估计值误差，‖ΩqtH-mt‖为艇体坐标系下磁场测量值与估计值误差。易知，使得误差函数f1(qt)和f2(qt)均取得极小值时的qt=[q0，q1，q2，q3]T，为最优姿态估计，这样转化为多目标最优化问题，确定如式(5)所示的优化问题来求得姿态数据

minF(qt)=minf1(qt)+minf2(qt).

(7)

因为f1(qt)和f2(qt)均大于等于0，根据式(7)中的每个目标函数的重要性，采用平方权函数法确定如下的目标函数

(8)

(9)

(10)

(11)

式(9)中γt决定了其收敛速率，所以，γt取值接近于艇体实际的姿态变化速率，取值如式(12)所示，避免步长过大导致姿态误差

(12)

3.3 姿态融合与专家系统

在3.1节中得到了由陀螺仪利用三轴角速率得到的四元数姿态，3.2节中利用梯度下降法得到的四元数姿态，然而实际应用中，陀螺仪会产生漂移，非静止或匀速状态下，加速度数据不能用于计算姿态角，再加上测量噪声的影响，因此，只依靠以上2种方法之一不能较好地估计姿态数据，需要将2种数据进行融合。本文采用常用的互补滤波器对2种数据进行实时融合，其常用的时域算法如下

qt=(1-αt)qgyr+αtqgra.

(13)

将式(4)和式(10)代入上式，并忽略极小项，简化后得到下式

(14)

考虑到艇体震动等有害加速度的影响，特提出专家系统规则，用于不同情况下根据运动状态自适应调整融合算法。

1)当a≤σ1时，艇体处于静止或匀速状态下，λ值不变；

2)当σ1

3)当a>σ2时，艇体处于高动态下，λ应取值0。

步骤(1)中融合算法提供的姿态是由加速度传感器和三轴磁强计对重力向量和磁向量的观测去补偿陀螺漂移和姿态角误差；步骤(2)，(3)中融合算法主要依赖于陀螺仪来估计姿态。σ1可根据加速度计的零漂值进行确定，而σ2应结合具体的应用条件确定，如σ2=1。

图4给出了整个系统的算法流程。可以看出，融合算法经推倒简化，最终只借助辅助传感器计算相应梯度值，每次迭代无需借助辅助传感器得到完整姿态，算法得到了优化。

4 实验结果

为验证所提出的无人飞艇航姿测量系统，将航姿系统安装在飞艇吊舱内，进行了静态和振动条件下的对比试验。为了进一步验证算法的有效性，结合飞艇运动的特点，进行了动态条件下本系统和高精度GPS惯性组合导航系统SPAN-CPT(姿态精度为±0.05°，方位角精度为±0.01°)的对比试验。

图5是静态条件下和振动条件下航姿系统采集到横滚角和俯仰角数据的对比。可以看出，振动条件下，航姿系统的姿态数据没有剧烈的跳动，航姿系统可以抑制一定艇体振动的影响。

图5 静态和振动条件下实验结果

图6是动态条件下本系统和SPAN-CPT组合导航定位系统同时采集的姿态数据对比。将SPAN-CPT系统采集到的数据作为参考值，本系统的采集的数据作为测量值，分别绘制了姿态变化曲线和误差曲线。从图6(a)，(c)中可以看出，二者输出的姿态数据趋势相同，基本吻合，只是在高动态下姿态误差较大，但基本在±2°以内，满足机动性较低的应用需求；对比曲线的水平段为静态数据，可以误差图中估计出系统的静态误差在±0.8°以内。

图6 动态下对比实验结果

5 结 论

本文研究了一种基于MEMS传感器的无人飞艇航姿测量方法。提出了基于梯度下降法的姿态融合方法，将加速度计和磁力计的数据用于校正陀螺仪估计的姿态，计算负荷小，速度快；针对振动干扰姿态问题，提出使用切比雪夫II型数字滤波器对加速度数据进行处理，从传感器数据处理和姿态解算过程双重抑制干扰。

通过多组实验，验证了文中的方法对于艇体震动和有害加速度具有明显的抑制作用，低动态下能有效地估计姿态，精度能满足无人飞艇飞行导航的应用要求。

参考文献:

[1] Markley F L.Attitude representation for Kalmanfiltering[C]∥Proceedings of the 2001 AAS/AIAA Astro Dynamics Specialists Conference,Guebec City,Guebec,Canada:AAS/AIAA,2001.

[2] Marins J L,Yun X,Bachmann E R,et al.An extended Kalman filter for quaternion-based orientation estimation using margsensors[C]∥Proc of IEEE/RSJ International Conference on Intelligent Robots and Systems,2001.

[3] 沈晓卫,姚敏立,赵 鹏.基于互补滤波的动中通天线姿态估计[J].中国惯性技术学,2011,19(2):194-197.

[4] 郭晓鸿,杨 忠,陈 喆,等.EKF和互补滤波器在飞行姿态确定中的应用[J].传感器与微系统，2011,30(11):149-152.

[5] 傅建国,王孝通,金良安,等.一种基于地球重力场和磁场的姿态估计新算法[J].电子学报,2005,33(3):567-570.

[6] 袁 信,郑 谔.捷联式惯性导航原理[M].北京:航空专业教材编审组,1985.

[7] Madgwick Sebastian O H,Harrison Andrew J L,Vaidyanathan Ravi.Estimation of IMU and MARG orientation using a gradient descent algorithm[C]∥Proceedings of IEEE International Conference on Rehabilitation Robotics Rehab Week Zurich,ETH Zurich Science City,Switzerland,2011.