广义凸条件下一类多目标优化问题的对偶
张瑞芳, 王海军
(太原师范学院 数学系, 太原 030012)
广义凸条件下一类多目标优化问题的对偶
张瑞芳, 王海军
(太原师范学院 数学系, 太原 030012)
凸性是最优化理论中最常用的假设之一。在实际应用中目标函数的性质可能不是那么理想,为了减弱凸性要求,人们给出了各种各样的广义凸性概念。近年来,广义凸性成为数学优化研究的新发展趋势,越来越多的学者致力于讨论在各种广义凸性条件下多目标优化问题的对偶结论及其应用。在广义凸条件之下考察一类多目标优化问题,首先介绍一类广义凸函数的概念及相关性质。然后建立了多目标优化问题(即原问题)的Wolfe对偶模型,在广义凸条件下得到了原问题与Wolfe对偶问题之间的弱对偶, 强对偶和逆对偶定理。最后建立了多目标优化问题的混合型对偶模型,并且得到了原问题的混合型对偶问题的弱对偶, 强对偶和逆对偶定理。
广义凸函数; 多目标优化; Wolfe对偶; 混合型对偶
0 引 言
凸性是最优化理论中最常用的假设之一,众所周知,凸函数是一类非常重要的函数,它具有一些良好的性质:如一个定义在凸集上的凸函数的局部极小值也是它的全局极小值;可微的凸函数在某点梯度向量为零,则函数在这一点取得最小值。正是由于凸函数的这些良好性质引起了学者们的注意,20世纪50年代初到60年代末人们对凸函数进行了大量深入细致的研究,并将凸函数应用到许多实际问题当中,使得凸分析和凸优化理论迅速发展起来。
然而,在实际应用中目标函数不一定是凸函数,因此,放宽凸性条件限制,推广凸函数的概念成为具有理论意义和现实应用背景的问题。近年来, 广义凸性成为数学优化研究的新发展趋势,人们给出了各种各样的广义凸性概念[1-15],值得提及的是1981年由Hanson[1]提出的不变凸性。在过去的20多年中不变凸性引起了众多学者的广泛注意,并对此概念做了许多推广。2012年3月,Cheng和Zhang在文献[7]中,首先给出d-ρ-(η,θ)-univex函数的概念,并在d-ρηθ-univex条件下讨论如下多目标优化问题(P):
其中:f:X→Rk;g:X→Rm;X为Rn的非空子集。
本文将在d-ρηθ-univex条件下建立问题(P)的Wolfe型对偶问题(WD)的弱对偶、强对偶、逆对偶结论以及问题(P)的混合型对偶问题(MD)的弱对偶、强对偶和逆对偶结论。
1 预备知识
本文采用Rn中向量之间序关系的惯用记号。设x=(x1,x2,…,xn),y=(y1,y2,…,yn)∈Rn,则有:xy⟺xiyi,(i=1,2,…,n),xy⟺xi≥yi,(i=1,2,…,n),x≯y代表xy的反面。相应地有类似的记号x 设η:X×X→Rn为一向量值函数,在本文中,用f′(u,η(x,u))表示f在η(x,u)方向的方向导数 在以下部分中b0:X×X→R+;φ0:R→R;η,θ:X×X→Rnn。 定义1[7]称函数f:X→R在点u∈X处关于b0,φ0为d-ρηθ-univex,若存在函数b0,φ0,η,θ以及实数ρ使得对于任意的x∈X有b0(x,u)φ0(f(x)-f(u))≥f′(u,η(x,u))+ρ‖θ(x,u)‖2。 若ρ0,则f(x)称为强d-ρηθ-univex;若ρ=0,则f(x)为d-univex;若ρ<0,则f(x)称为弱d-ρηθ-univex。 定义2[7]称函数f:X→R在点u∈X处关于b0,φ0为弱严格伪d-ρηθ-univex,若存在函数b0,φ0,η,θ以及实数ρ使得对于任意的x∈X有 b0(x,u)φ0(f(x)-f(u))<0⟹f′(u,η(x,u))+ρ‖θ(x,u)‖2<0。 首先作如下假设: b00;φ0(t)<0对任意的t<0成立。 关于原问题(P)应考虑它的Wolfe对偶(WD): 定理1(弱对偶) 设x,(y,ξ,μ)分别是(P)和(WD)的可行点,若进一步假设ξTf+μTg关于b0,φ0为弱严格伪d-ρηθ-univex函数;且ρ≥0,则f(x)≮φ(y,ξ,μ)。 ξTf(x)<ξTf(y)+μTg(y) ξTf(x)+μTg(x)<ξTf(y)+μTg(y) 由于b00;φ0(t)<0 对任意的t<0成立,可得 b0(x,u)φ0(ξTf(x)+μTg(x)-ξTf(y)-μTg(y))<0 由已知ξTf+μTg关于b0,φ0为弱严格伪d-ρηθ-univex函数,于是 ξTf′(y,η(x,y))+μTg′(y,η(x,y))+ρ‖θ(x,y)‖2<0 而ρ≥0,故ξTf′(y,η(x,y))+μTg′(y,η(x,y))<0,与对偶约束条件式(4)相矛盾,即证明了f(x)≮φ(y,ξ,μ)。证毕。 在这一部分,考虑原问题(P)的混合型对偶: ξTf(x)<ξTf(y)+μTg(y) ξTf(x)+μTg(x)<ξTf(y)+μTg(y) 由于b00;φ0(t)<0 对任意的t<0成立,可得 b0(x,u)φ0(ξTf(x)+μTg(x)-ξTf(y)-μTg(y))<0 由已知ξTf+μTg关于b0,φ0为弱严格伪d-ρηθ-univex函数,于是 ξTf′(y,η(x,y))+μTg′(y,η(x,y))+ρ‖θ(x,y)‖2<0 而ρ≥0,故ξTf′(y,η(x,y))+μTg′(y,η(x,y))<0,与对偶约束条件式(6)相矛盾,即证明f(x)≮φ(y,ξ,μ)。证毕。 本文在d-ρηθ-univex条件下建立问题(P)的Wolfe型对偶问题(WD)的弱对偶, 强对偶,逆对偶结论以及问题(P)的混合型对偶问题(MD)的弱对偶,强对偶和逆对偶结论。今后还可以进一步讨论d-ρηθ-univex条件下的分式规划问题及其对偶。 [ 1 ]HANSON M A. On sufficiency of Kuhn-Tucker conditions[J]. J Math Anal Appl, 1981,80(2):545-550. [ 2 ]YE Y L.d-invexity and optimality conditions[J]. J Math Anal Appl, 1991,162(2):242-249. [ 3 ]ZALMAI G J. Generalized sufficiency criteria incontinuous-time programming with application to a class of variational-type inequalities[J]. J Math Anal Appl, 1990,153(3):331-355. [ 4 ]ANTCZAK T. Multiobjective programming underd-invexity[J]. Eur J Oper Res, 2002,137(1):28-36. [ 5 ]MISHRA S K, WANG S Y, LAI K K. Nondifferentiable multiobjective programming under generalized d-univexity[J]. Eur J Oper Res , 2005,160(1):218-226. [ 6 ]NAHAK C, MOHAPATRA R N.d-ρ-(η,θ)-invexity in multiobjective optimization[J]. Nonlinear Anal, 2009,70(6):2288-2296. [ 7 ]程曹宗,张瑞芳. 一类广义univex条件下的多目标优化[J]. 北京工业大学学报, 2012,38(3):467-472. [ 8 ]MISHRA S K, WANG S Y, LAI K K. Optimality and duality for multiple-objective optimization under generalized type I univexity[J]. J Math Anal Appl, 2005,303(1):315-326. [ 9 ]王立柱. 非线性优化中关于鞍点及对偶问题的研究[J]. 沈阳师范大学学报:自然科学版, 2008,26(3):272-274. [10]ZHANG X H, CHENG C Z. Some Farkas-type results for fractional programming problems with DC functions[J]. Nonlinear Anal, 2009,10(3):1679-1690. [11]ANTCZAK T. (p,r)-Invex sets and functions[J]. J Math Anal Appl, 2001,263(2):355-379. [12]ANTCZAK T. On (p,r)-invexity-type nonlinear programming problems[J]. J Math Anal Appl, 2001,264(2):382-397. [13]ANTCZAK T. A Class of B-(p,r)-invex functions and mathematical programming[J]. J Math Anal Appl, 2003,286(1):187-206. [14]ANTCZAK T. Relationships between pre-invex concepts[J]. Nonlinear Anal, 2005,60(2):349-367. [15]ANTCZAK T.r-Pre-invexity andr-invexity in Mathematical Programming[J]. Comput Math Appl, 2005,50:551-566. Dualityforakindofmultiobjectiveoptimizationproblemundergeneralizedconvexity ZHANGRuifang,WANGHaijun (Department of Mathematics, Taiyuan Normal University, Taiyuan 030012, China) Convexity is the most commonly used hypothesis in optimization theory. In the practical application, the property of objective function is not so ideal. In order to relax the convexity condition, people provide various of generalized convexity concepts. In recent years, generalized convexity become the new trend of mathematical optimization, more and more scholars devote to discuss multiobjective optimization problem duality results and its applications under generalized convexity. This paper considers a kind of multiobjective optimization problem under generalized convexity condition. Firstly, we introduce the concept of a kind of generalized convexity and related properties. Then we set up Wolfe dual problem of the original multiobjective optimization problem. Weak, strong and converse duality results between the original problem and its Wolfe dual problem are given. Finally we establish mixed type dual problem of the original problem, and obtain weak, strong and converse duality between the original problem and its mixed type dual problem. generalized convex function; multiobjective optimization; Wolfe duality; mixed type duality 2013-10-01。 国家自然科学基金资助项目(11171250)。 张瑞芳(1982-),女,山西交口人,太原师范学院教师,硕士。 1673-5862(2014)04-0482-04 O221.6 : A 10.3969/ j.issn.1673-5862.2014.04.006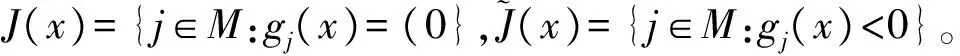
2 Wolfe对偶
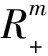
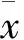
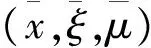
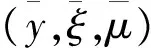
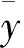
3 混合型对偶
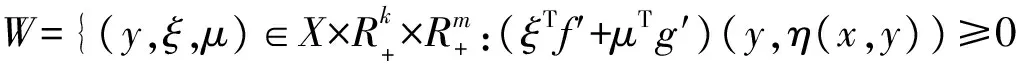
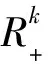
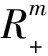
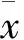
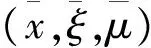
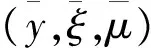
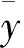
4 结 论

