带有不可用区间中断可恢复的平行机排序问题

张 琦, 罗成新

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

带有不可用区间中断可恢复的平行机排序问题

张 琦, 罗成新

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

讨论带有不可用区间且工件中断可恢复的两台平行机排序问题。其中一台机器带有不可用区间,在不可用区间内不能加工工件。工件在加工时被不可用区间中断后,可以在不可用区间之后继续加工。目标是最小化加权总完工时间。这个问题是一般定义下NP-难的,因此需要寻找满足指定精确度的近似解。首先给出全多项式近似方案的定义,其次提出了一个动态规划的算法,最后利用划分程序的方法得到了一个全多项式近似方案(FPTAS),该近似方案的时间复杂性为O(n5L5/ε4),其中:n为输入工件的个数;L为输入规模;ε0为误差精度。

平行机排序; 不可用区间; 中断可恢复; NP-难; 全多项式近似方案

0 引 言

对于经典排序问题大多数做如下假设:任何时间机器都是可以加工工件的。但是在实际生产过程这种假设条件不能总被满足。例如:在机器发生故障或定期维修、保养的一时间段内不能加工工件,即产生了不可用区间,通常将这类问题称为机器具有可用性限制问题。如果一个工件在不可用区间之前不能完工,那么该工件可以在不可用区间之后继续加工,称该工件是中断可恢复的。Lee[1]考虑了不同的机器有可用性限制的排序问题。Ji[2]研究的是工件带有线性退化加工时间的平行机排序问题。此外,文献[3-9]对相应的问题分别得到了全多项式时间近似方案。文献[10-14]研究的也是带有不可用区间的排序问题。

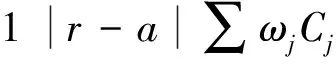
1 问题描述

该问题是在2台平行机上将工件集J={1,2,…,n}中的n个互不相关工件进行排序,目标是最小化加权总完工时间。每个工件i∈J的加工时间为pi。假设第1台机器一直可用且第2台机器在区间[T2,S2]内不能加工工件,机器在每一时刻至多能加工一个工件。不失一般性,考虑所有的数据都是正整数。将工件先按WSPT规则排好(即ω1/p1≥ω2/p2≥…≥ωn/pn)。这里仅考虑所有工件不全都排在第1台机器上且不能全都排在第2台机器T2之前的情形。

2 全多项式近似方案

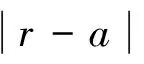
由引理1,本文的排序问题P2/r-a∑ωjCj的最优解中,每台机器上的工件都按ωj/pj非增的顺序排列。将所有工件按ω1/p1≥ω2/p2≥…≥ωn/pn排列。引入变量xj(j=1,2,…,n),如果工件Jj在第1台机器上加工,令xj=1;如果工件Jj在第2台机器T2之前加工,令xj=2;如果工件Jj在第2台机器S2之后加工,令xj=3。记X为所有向量x=(x1,x2,…,xn)所组成的向量集,其中xj={1,2,3},j=1,2,…,n。定义在集合X上的函数如下:

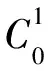
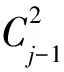
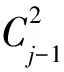
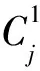
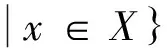
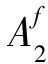
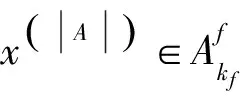
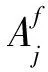
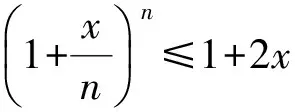
对于问题P2/r-a∑ωjCj给出一个FPTAS。

算法Aε

第1步 将工件按ω1/p1≥ω2/p2≥…≥ωn/pn顺序排列。令Y0={(0,…,0)},j=1。

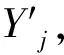
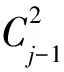
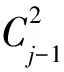
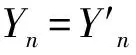
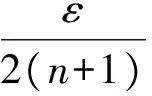
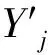
hj(x(a1,a2,a3,b))=min{hj(x):x∈Ya1,a2,a3,b}

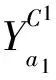
置j=j+1,转第2步。

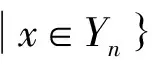
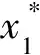
定理1 问题P2/r-a∑ωjCj利用算法Aε,在O(n5L5/ε4)运行时间内找到一向量x′∈X使得h(x′)≤(1+ε)h(x*),其中x*是最优解。

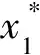
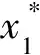
当xj=1时,

当xj=2时,

当xj=3时,

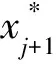
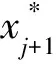
这样导出

从式(1)和式(6)得

类似地有

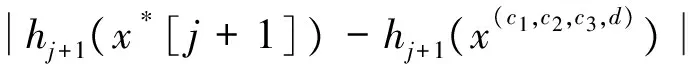
令δk=δ+δk-1(1+δ),k=2,3,…,n-j+1。那么有

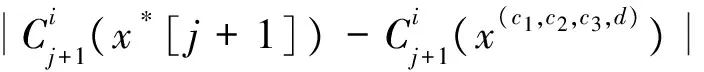
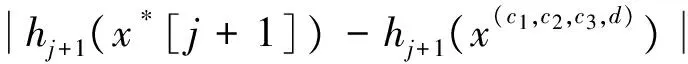
对j+2,…,n重复论证,有x′∈Yn,得到

又通过引理4有

因此

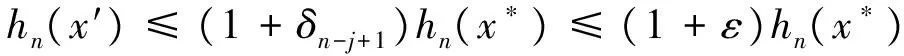
因此,通过算法Aε中的第3步,得到的x0满足

hn(x0)≤hn(x′)≤(1+ε)hn(x*)

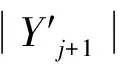
3 结 论

本文考虑的是一台机器在某固定时间内不可用且工件中断可恢复的两台平行机排序问题,目标是最小化加权总完工时间,对该问题给出了一个全多项式方案(FPTAS),其时间复杂性为O(n5L5/ε4)。

[ 1 ]LEE C Y. Machine scheduling with an availability constraint[J]. J Global Optim, 1996,9(3/4):395-416.

[ 2 ]JI Min, CHENG T C E. Parallel-machine scheduling with simple linear deterioration to minimize total completion time[J]. Eur J Oper Res, 2008,188(2):342-347.

[ 3 ]KOVALYOV M Y, KUBIAK W. A fully polynomial approximation scheme for the weighted earliness-tardiness problem[J]. Oper Res, 1999,47(5):757-761.

[ 4 ]KOVALYOV M Y, KUBIAK W. A fully polynomial approximation scheme for minimizing makespan of deteriorating jobs[J]. J Heuristics, 1998,3(4):287-297.

[ 5 ]WU C C, LEE W C. Scheduling linear deteriorating jobs to minimize makespan with an availability constraint on a single machine[J]. Inf Process Lett, 2003,87(2):89-93.

[ 6 ]KELLERER H, STRUSEVICH V A. A fully polynomial approximation scheme for the single machine weighted total tardiness problem with a common due date[J]. Theor Comput Sci, 2006,369(1):230-238.

[ 7 ]KACEM I. Approximation algorithms for the makespan minimization with positive tails on a single machine with a fixed non-availability interval[J]. J Comb Optim, 2009,17(2):117-133.

[ 8 ]KACEM I. Fully polynomial time approximation scheme for the total weighted tardiness minimization with a common due date[J]. Discrete Appl Math, 2010,158(9):1035-1040.

[ 9 ]乔玉,罗成新. 具有禁用区间的平行机排序时间表长问题的全多项式近似方案[J]. 沈阳师范大学学报:自然科学版, 2012,30(1):12-15.

[10]LEE C Y. Parallel machines scheduling with non-simultaneous machine available time[J]. Discrete Appl Math, 1991,30:53-61.

[11]LEE C Y, DANUSAPUTRO L S. Capacitated two-parallel machines scheduling to minimize sum of job completion times[J]. Discrete Appl Math, 1993,41(3):211-222.

[12]LI Shisheng, YUAN Jinjiang. Parallel-machine scheduling with deteriorating jobs and rejection[J]. Theor Comput Sci, 2010,411(40):3642-3650.

[13]KELLERER H, KUBZIN M A, STRUSEVICH V A. Two simple constant ratio approximation algorithms for minimizing the total weighted completion time on a single machine with a fixed non-availability interval[J]. Eur J Oper Res, 2009,199(1):111-116.

[14]ZOU Juan, ZHANG Yuzhong, MIAO Cuixia. Uniform parallel-machine scheduling with time dependent processing times[J]. J Oper Res Soc, 2013,1(2):239-252.

[15]GRAHAM R L, LAWLER E L, LENSTRA J K, et al. Optimization and approximation in deterministic sequencing and scheduling: a survey[J]. Ann Discrete Math, 1979,5:287-326.

Parallelmachineschedulingproblemwitharesumableavailabilityconstraint

ZHANGQi,LUOChengxin

(School of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)

This paper considers a scheduling problem of two parallel machines with a resumable availability constraint. The machine is unavailable betweenT2andS2. We call a job resumable if it cannot finish before the unavailable period of a machine and can continue after the machine is available again. The objective is to minimize the sum of weighted completion times. The problem is NP-hard in the ordinary sense. Therefore, we need to find an approximate solution that fulfills the required error bound. Firstly we propose the definition of the fully polynomial-time approximation scheme. Secondly we give a dynamic programming algorithm. Finally we obtain a fully polynomial-time approximation scheme (FPTAS) by procedure partition. Its running time isO(n5L5/ε4), wherenis the number of jobs,Lis the input size andεis the required error bound.

parallel machine scheduling; non-availability interval; resume; NP-hard; FPTAS

2014-03-16。

国家自然科学基金资助项目(61070242)。

张 琦(1989-),女,辽宁沈阳人,沈阳师范大学硕士研究生;

: 罗成新(1958-),男,辽宁新宾人,沈阳师范大学教授,博士,硕士研究生导师。

1673-5862(2014)04-0466-05

O223

: A

10.3969/ j.issn.1673-5862.2014.04.003