MATLAB软件可视化效果在大学数学中的应用
孙 欣, 冯 艳, 吴志丹, 王 涛
(1. 沈阳师范大学 数学与系统科学学院, 沈阳 110034; 2. 沈阳师范大学 计算机与数学基础教学部, 沈阳 110034)
MATLAB软件可视化效果在大学数学中的应用
孙 欣1, 冯 艳2, 吴志丹2, 王 涛2
(1. 沈阳师范大学 数学与系统科学学院, 沈阳 110034; 2. 沈阳师范大学 计算机与数学基础教学部, 沈阳 110034)
与传统的大学数学课堂教育相比较,MATLAB这种计算机数学语言将实验数据或计算结果用图形的方式直观地显示出来,可以将难以显示的隐含数直接用曲线描绘出来,在大学数学课堂教学中有效地解决了数学的高度抽象性问题。在大学数学公共课的教学实践中,利用MATLAB软件提供的数学语句在线性代数、概率论与数理统计及高等数学3门课上绘制图形,帮助学生有效理解、掌握大学数学教学中较为生涩、抽象的概念、定义、定理及推论。将教学实践成果加以整理,以实例演示说明MATLAB软件的可视化在大学数学教学中有效地创设学习情境,提高学习效率,取得事半功倍的效果。
MATLAB软件; 可视化效果; 大学数学
0 引 言
MATLAB是一种用于科学工程计算的高效率高级语言,原是提供使用LINPACK(线性代数软件包)和EISPACK(基于特征值计算的软件包)软件包接口的,后来逐渐发展成通用科学计算、图视交互系统和程序设计语言。与BASIC、FORTRAN、C/C++等语言相比,MATLAB的语法规则简单,更贴近人的思维方式,被称为“演算纸式的”科学工程算法语言[1]。MATLAB应用在数值计算、数字信号处理、系统识别、自动控制、神经网络控制、动态仿真系统、特殊函数和图像领域。MATLAB也广泛应用在高等应用问题的求解中,如:微积分问题的计算机求解、线性代数问题的计算机求解、代数方程与最优化问题的计算机求解、微分方程问题的计算机求解、概率论与数理统计问题的计算机求解等[2]。MATLAB的绘图功能具有非常强的实用性和可视性[3],绘图命令不仅简单明了,而且控制和表现数据图形的能力强。
1 MATLAB可视化效果在线性代数上的应用
线性代数是大学本科计算机、工程、管理、经济各专业必修的基础课,由于本课程具有较强的抽象性,所以教学中数学实验的演示有助于对课程内容的理解。本文以二次型的教学为例,说明MATLAB可视化效果的应用。通常,国内各种教材通常利用线性变换等知识来讲解二次型;而国外教材[4]利用数、形结合的方法,即用可视化的图形将所学的内容直观呈现出来,将形象思维和抽象思维结合起来,这符合认知规律。本文从2个方面说明MATLAB可视化效果在线性代数上的应用。
1.1利用正交变换化二次型为标准型时保持几何形状不变
例1 利用正交变换将二次型f(x,y)=x2-8xy-5y2化成标准型。
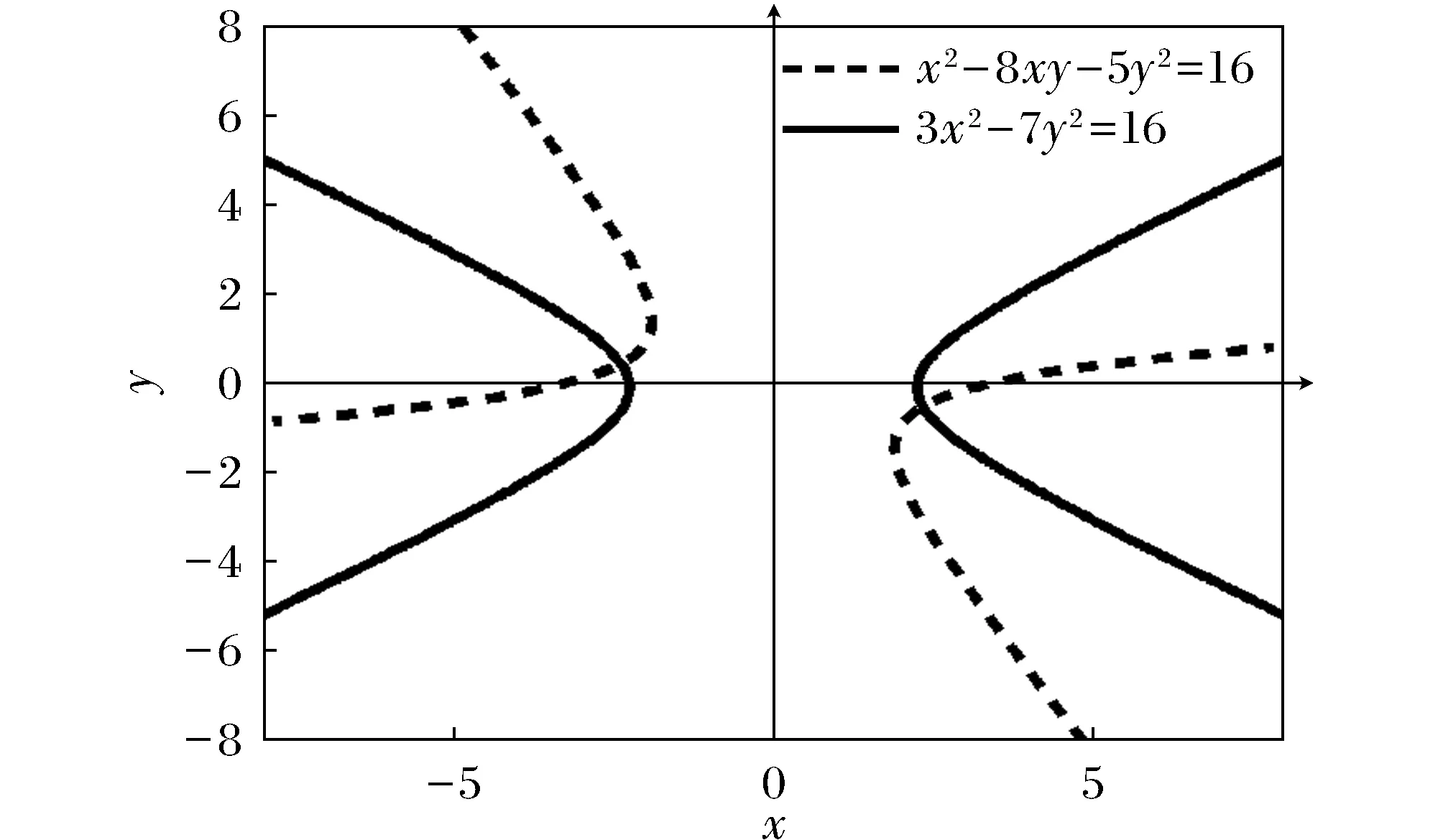
图1 旋转前后的双曲线

注释1 由图1可以看出,二次曲线在正交变换的作用下几何图形保持不变,这是正交变换的意义。
1.2正(负)定二次型的意义
教材[5]对正(负)定二次型定义是这样描述的:设有二次型f(x)=xTAx,A是对称矩阵,如果对于任意的x≠0,都有f(x)0 (f(x)<0),则称f(x)为正(负)定二次型。这种从代数角度描述正(负)定二次型理解起来较抽象,如果借助可视化,利用图形演示直观看到,有助于概念的理解。
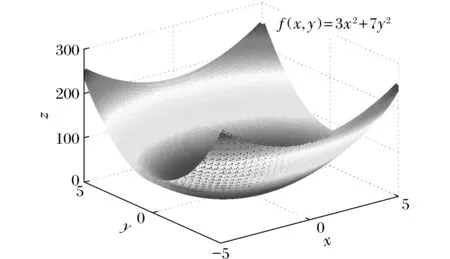
图2 正定二次型
例2 利用MATLAB三维图形语句绘制正定二次型f(x,y)=3x2+7y2。
利用MATLAB三维图形绘制语句[x,y]=meshgrid(-5∶0.1∶5,-5∶0.1∶5);z=3*x.^2+7*y.^2;mesh(x,y,z)画出图形,如图2所示。
由图2可以看出,当(x,y)≠0时,正定二次型3x2+7y20。
同理,利用MATLAB三维图形语句绘制负定二次型f(x,y)=-3x2-7y2。
由图3可以看出,当(x,y)≠0时,负定二次型-3x2-7y2<0。
利用MATLAB三维图形语句绘制不定二次型f(x,y)=3x2-7y2。
由图4可以看出,当(x,y)≠0时,不定二次型3x2-7y20或3x2-7y2<0。
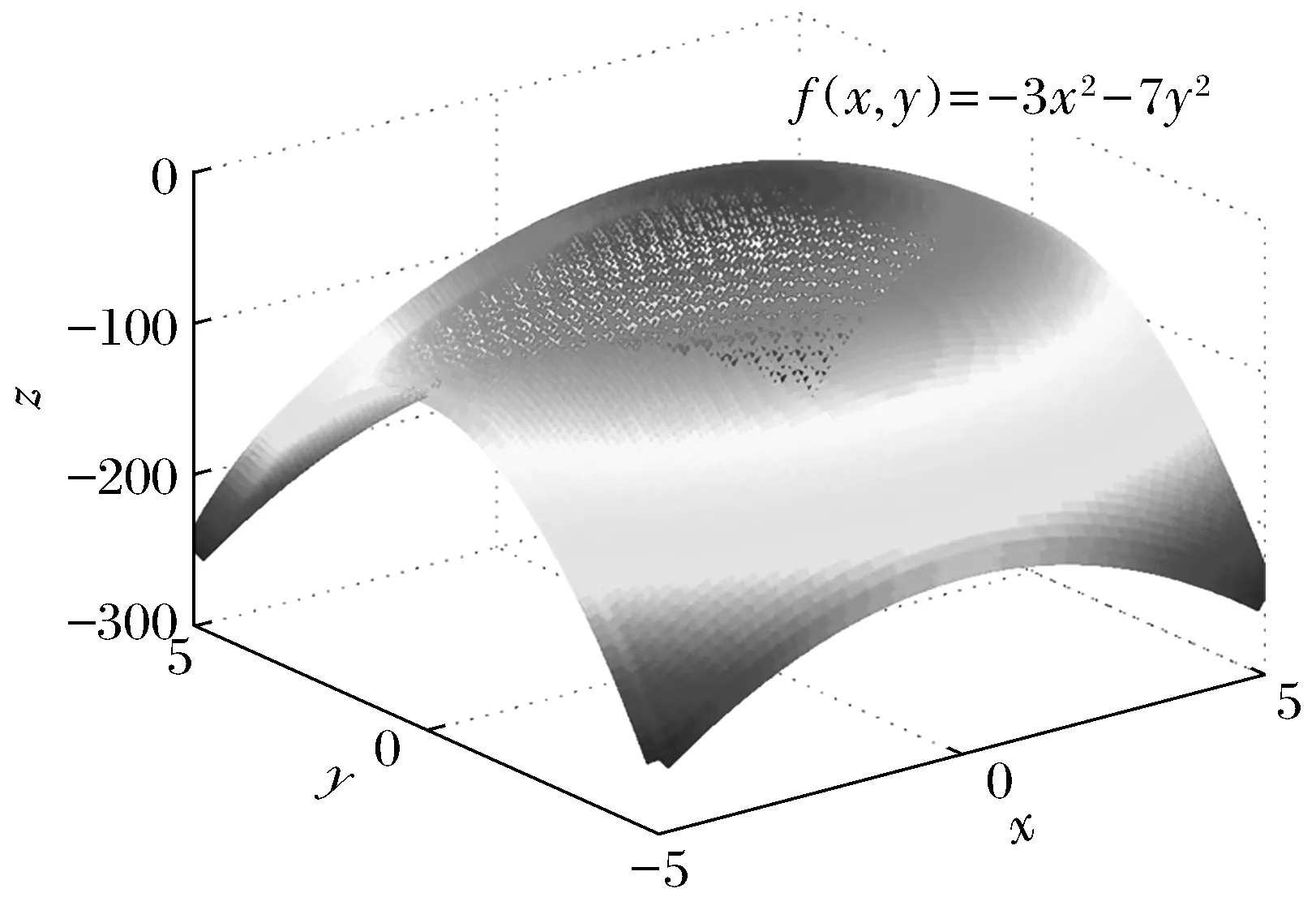
图3 负定二次型

图4 不定二次型
注释2 利用MATLAB可视化效果,对正(负)定二次型概念有了清晰的认识。
2 MATLAB可视化效果在概率论与数理统计上的应用
概率论与数理统计是大学数学专业一门基础课程。课程中一些抽象、生涩的概念和定义给学习带来许多困难,国外教材[6-7]通常利用数学实验产生直观可视的图形和图像帮助对知识的理解。本文作者在文献[8]中从3个方面说明MATLAB可视化效果在概率论与数理统计中的应用,详细内容见文献[8]。
3 MATLAB可视化效果在高等数学上的应用
MATLAB提供了一系列直观、简单的绘图命令与函数,将高等数学中一些复杂函数用图形显示出来,有助于分析和研究函数的性质。下面从2个方面加以说明。
3.1求函数的渐近线
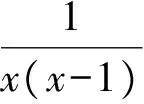

图5 曲线f(x)=及其铅直渐近线
因为
所以x=0,x=1是曲线的两条铅直渐近线。
利用MATLAB语句:
ezplot(′x*(x-1)*y=1′,[-10 10])画出图形5。
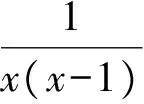

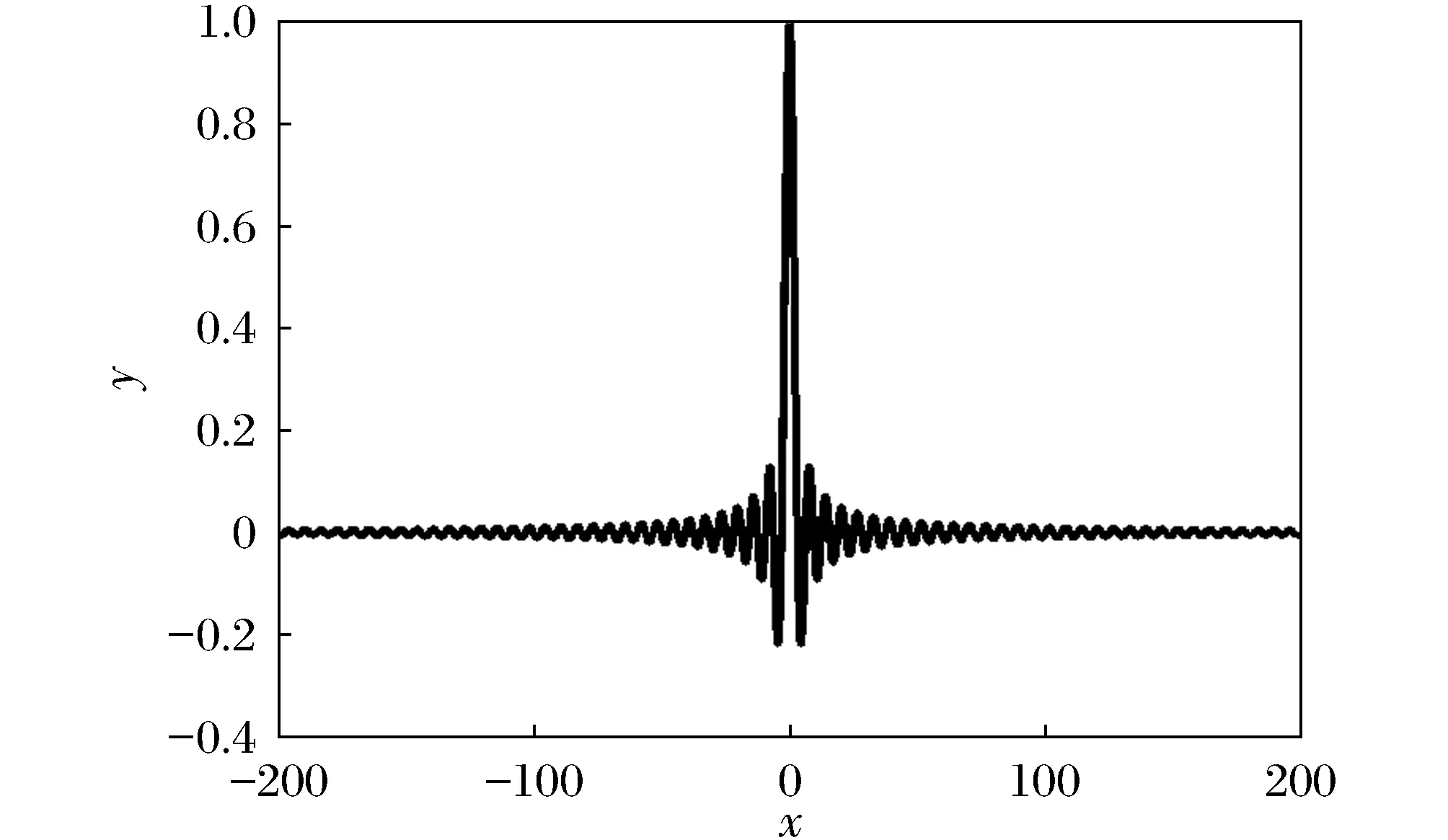
图6 曲线f(x)=及其水平渐近线
因为
所以y=0是曲线的一条水平渐近线。
利用MATLAB语句:x1=[0.001:0.01:200];y1=sin(x1)/x1;plot(x1,y1);hold onx2=[-200:0.01:-0.0001];y2=sin(x2)./x2;plot(x2,y2)画出图形6。

3.2将函数展成幂级数
无穷级数是逼近理论中重要内容,是研究函数性质以及进行数值计算的非常有用的数学工具。通常,多项式被选为比较简单的函数作为近似函数,一是因为多项式函数形式简单规范,适合用计算机来计算其值,二是这类函数是连续的,并且具有各阶导数,具有极好的分析性质。因此当我们用多项式函数来近似地表示一个已知函数时很方便[9]。
例5 将函数f(x)=ex展成x的幂级数。
由高等数学相关知识[10],得到
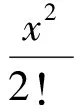
利用MATLAB语句:x=[-2:0.01:10];y1=exp(x);plot(x,y1);hold ony2=1+x+1/2*x.^2+1/6*x.^3;plot(x,y2);hold ony3=1+x+1/2*x.^2;plot(x,y3);hold ony4=1+x;plot(x,y4);画出图形7。

图7 将函数ex展成x的幂级数比照图
注释5 由图7不难发现,随着多项式展开式项数的增加,在点(0,1)的局部范围内,多项式函数越来越逼近ex,借助MATLAB可视化图形,对幂级数理论有了直观认识。
4 结论与展望
遵循数学学习中数形结合的方法,以及抽象思维与形象思维相结合的认知规律,本文研究了MATLAB可视化效果在大学三门重要的基础课程:线性代数、概率论与数理统计和高等数学教学中的应用,力求起到抛砖引玉的作用。MATLAB语言可以用一系列简单、直观的绘图语句将实验数据和仿真结果用可视的方式显示出来。若充分、恰当地将MATLAB软件的可视化引进大学数学课堂教学,长期坚持会起到事半功倍的效果。
[ 1 ]尹泽明,丁春利. 精通MATLAB 6[M]. 北京:清华大学出版社, 2002.
[ 2 ]薛定宇,陈阳泉. 高等应用数学问题的MATLAB求解[M]. 北京:清华大学出版社, 2004.
[ 3 ]马秀麟,赵国庆,朱艳涛. 知识可视化与学习进度可视化在LMS中的技术实现[J]. 中国电化教育, 2013(1):121-125.
[ 4 ]DAVID C L. 线性代数及其应用[M]. 北京:机械工业出版社, 2006.
[ 5 ]同济大学数学系. 工程数学:线性代数[M]. 5版. 北京:高等教育出版社, 2007.
[ 6 ]JAY L D. 概率论与数理统计[M]. 5版. 北京:高等教育出版社, 2008.
[ 7 ]SHELDON. 概率论基础教程[M]. 6版. 赵选民,译. 北京:机械工业出版社, 2006.
[ 8 ]孙欣,陈文英,吴志丹,等. 基于MATLAB可视化的概率问题求解[J]. 沈阳师范大学学报:自然科学版, 2010,28(4):487-490.
[ 9 ]同济大学应用数学系. 微积分:下册[M]. 北京:高等教育出版社, 2003.
[10]同济大学数学系. 高等数学:下册[M]. 6版. 北京:高等教育出版社, 2007.
ApplicationofMATLABvisualizationeffectinuniversitymathematicsteaching
SUNXin1,FENGYan2,WUZhidan2,WANGTao2
(1. School of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China; 2. Department of Computer and Mathematics Teaching, Shenyang Normal University, Shenyang 110034, China)
Compared with the traditional class teaching of university mathematics, MATLAB called as a computer mathematical language can visualize the experimental data or the computation results into the graphics and draw the implicit function with the curve, which is efficient to solve the abstractness of mathematics. In the teaching practice of the university mathematics, applying the mathematical language via MATLAB into the drawing of Linear Algebra, Probability and Statistics and Calculus teaching, it is helpful for students to understand and grasp the obscure and abstract concepts, definitions, theorems and corollaries. Then the results of teaching practice are sorted out and the examples are illustrated to show that MATLAB visualization in university mathematics teaching is beneficial to create perfect study scene and increase study efficiency.
MATLAB software; visualization effect; university mathematics
2014-06-06。
辽宁省高等学校杰出青年学者成长计划(LJQ2011118); 辽宁省自然科学基金资助项目(201202201); 沈阳师范大学教育教学改革研究项目(JG2012-YB042)。
孙 欣(1972-),女,辽宁沈阳人,沈阳师范大学副教授,博士。
1673-5862(2014)04-0549-04
G434
: A
10.3969/ j.issn.1673-5862.2014.04.021

