具有学习效应的排序问题的某些新进展
赵 传 立
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
具有学习效应的排序问题的某些新进展
赵 传 立
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
Biskup 首先将学习效应的的概念引入到排序问题中,并且在2008年给出具有学习效应的排序问题的全面综述。从此以后,具有学习效应的排序问题持续引起研究者的兴趣。除了Biskup综述所提到的模型外,文献中还有其他学习效应模型,对近年来文献中出现的具有学习效应的排序模型做一简要介绍。主要考虑3类模型:工件的实际加工时间依赖于具体的位置函数的模型,工件的实际加工时间依赖于抽象的位置函数的模型,工件的实际加工时间依赖于截断式学习函数的模型。
排序; 学习效应; 单机; 平行机; 流水作业
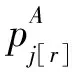
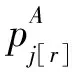
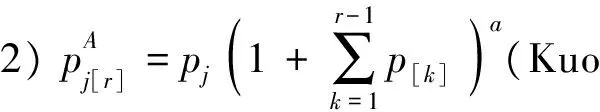
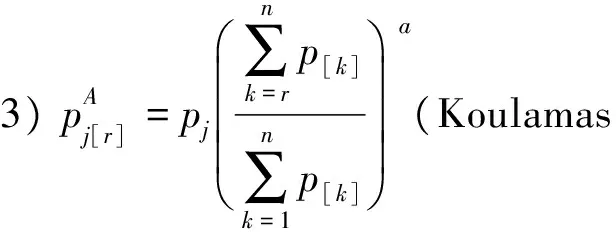
作为新型排序的一个组成部分,具有学习效应的排序问题持续受到研究者的关注。在Biskup的综述之后,近年又出现了许多新模型。这些新模型一部分是利用已有模型加以组合而成,另一部分则是对已有模型做某些推广。本文仅介绍后一类模型,关注2009年以后的某些研究进展。主要介绍各个模型中常见目标函数在一般情况下的结论,关注多项式最优算法,不涉及启发式算法、分支定界法等。对于特殊情况和特殊目标函数的有关结论不做介绍。
1 主要模型
主要介绍近年来产生的3类新模型:工件的实际加工时间是具体函数的模型,工件的实际加工时间是抽象函数的模型,工件的实际加工时间是截断式学习函数的模型。
1.1工件的实际加工时间是具体函数的模型

表1 加工时间是具体函数的模型
续表1

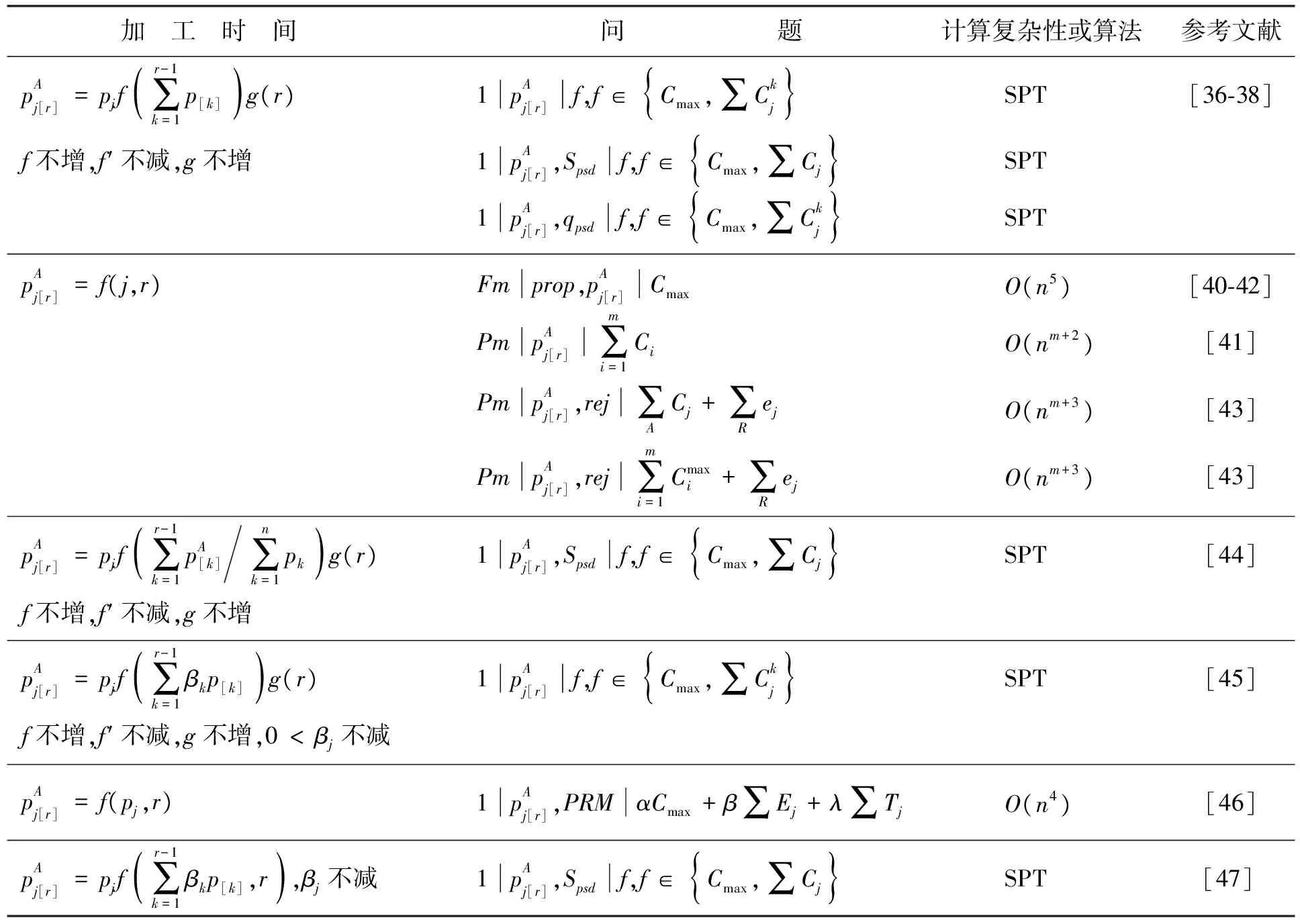
加 工 时 间 问 题 计算复杂性或算法参考文献pAj[r]=pj(αa∑r-1k=1p[k]+β)1pAj[r],SpsdfSPT[16]α≥0,β≥0,0 1.2工件的实际加工时间是抽象函数的模型 表2 加工时间是抽象函数的模型 续表2 加 工 时 间 问题计算复杂性或算法 参考文献pAj[r]=pjf(∑r-1k=1p[k])g(r)1pAj[r]f,f∈{Cmax,∑Ckj}SPT[36⁃38]f不增,f′不减,g不增1pAj[r],Spsdf,f∈{Cmax,∑Cj}SPT1pAj[r],qpsdf,f∈{Cmax,∑Ckj}SPTpAj[r]=f(j,r)Fmprop,pAj[r]CmaxO(n5)[40⁃42]PmpAj[r]∑mi=1CiO(nm+2)[41]PmpAj[r],rej∑ACj+∑RejO(nm+3)[43]PmpAj[r],rej∑mi=1Cmaxi+∑RejO(nm+3)[43]pAj[r]=pjf(∑r-1k=1pA[k]∑nk=1pk)g(r)1pAj[r],Spsdf,f∈{Cmax,∑Cj}SPT[44]f不增,f′不减,g不增pAj[r]=pjf(∑r-1k=1βkp[k])g(r)1pAj[r]f,f∈{Cmax,∑Ckj}SPT[45]f不增,f′不减,g不增,0<βj不减pAj[r]=f(pj,r)1pAj[r],PRMαCmax+β∑Ej+λ∑TjO(n4)[46]pAj[r]=pjf(∑r-1k=1βkp[k],r),βj不减1pAj[r],Spsdf,f∈{Cmax,∑Cj}SPT[47] 1.3工件的实际加工时间是截断式的模型 表3 截断式学习效应模型 续表3 加 工 时 间 问题计算复杂性或算法 参考文献pAj[r]=pjmax{raj,β},0<β<11pAj[r],CON∑(αEj+βTj+γd)O(n3)[57]1pAj[r],SLK∑(αEj+βTj+γdj)1pAj[r]ff∈{Cmax,∑Cj,∑∑Ci-CjpAj[r]=pjmax{(1-∑r-1k=1p[k]∑nk=1p[k])a,β}1pAj[r]f,f∈{Cmax,∑Cj}SPT[58]a>1,0<β<1pAj[r]=pjmax{(aα-∑r-1k=1p[k]∑nk=1pk+b),β}1pAj[r]f,f∈{Cmax,∑Ckj}SPT[60]a≥0,b≥0,a+b=1,a≥1,0<β<1 关于具有学习效应的排序问题还有许多结论,限于本文涉及内容和资料的局限,不可能完全提及。即使对于提到的模型的结论也难免挂一漏万,因此文中内容仅供感兴趣的读者参考。从上节所提各个模型的研究成果来看,对于工件的实际加工时间是具体函数的模型,虽模型较多,但研究结论主要集中在单机问题。具有一般性结论的目标函数主要是最大完工时间和完工时间和,且所用方法是常见的SPT规则。对于工件的实际加工时间是抽象函数的模型,某些模型的研究结果还相对较少,有些主要集中在某一具体机器环境的特定目标函数。对于截断式学习效应的排序模型,由于提出的时间相对较短,目前研究成果相对较少。在未来的工作中,对于各个模型可以考虑如下研究方向:对于实际加工时间是具体函数的模型,针对具体模型的机器环境是平行机还是车间作业,研究目标函数范围更广泛的问题;对于工件的实际加工时间是抽象函数的模型,可研究包括多个具体函数的抽象函数模型,使其结论具有一般性;对于截断式学习效应的排序模型,根据不同的加工时间函数,考虑其他形式的阶段学习效应模型。 [ 1 ]BISKUP D. Single-machine scheduling with learning considerations[J]. Eur J Oper Res, 1999,115(1):173-178. [ 2 ]BISKUP D. A state-of-the-art review on scheduling with learning effects[J]. Eur J Oper Res, 2008,188(2):315-329. [ 3 ]MOSHEIOV G, SIDNEY J B. Scheduling with general job-dependent learning curves[J]. Eur J Oper Res, 2003,147(3):665-670. [ 4 ]KUO W H, YANG D L. Minimizing the total completion time in a single-machine scheduling problem with a time-dependent learning effect[J]. Eur J Oper Res, 2006,174(2):1184-1190. [ 5 ]KOULAMAS C, KYPARISIS G J. Single-machine and two-machine flowshop scheduling with general learning function[J]. Eur J Oper Res, 2007,178(2):402-407. [ 6 ]JIANG Zhongyi, CHEN Fangfang, WU Chunqing. Minimizing the maximum lateness in a single-machine scheduling problem with the normal time-dependent and job-dependent learning effect[J]. Appl Math Comput, 2012,218(18):9438-9441. [ 7 ]JIANG Zhongyi, CHEN Fangfang, KANG Huiyan. Single-machine scheduling problems with actual time-dependent and job-dependent learning effect[J]. Eur J Oper Res, 2013,227(1):76-80. [ 8 ]CHENG T C E, KUO W H, YANG D L. Scheduling with a position-weighted learning effect[J]. Optim Lett, 2014,8(1):293-306. [ 9 ]LEE W C, WU C C. Some single-machine and m-machine flowshop scheduling problems with learning considerations[J]. Inf Sci, 2009,179(22):3885-3892. [10]LEE W C, LAI P J, WU C C. Erratum to “Some single-machine and m-machine flowshop scheduling problems with learning considerations”[J]. Inf Sci, 2010,180(6):799-1073. [11]KUO W H, YANG D L. Note on “Single-machine and flowshop scheduling with a general learning effect model” and “Some single-machine and m machine flowshop scheduling problems with learning considerations”[J]. Inf Sci, 2010,180(19):3814-3816. [12]WANG Jibo, WU Yubin, JI Ping. A revision of some single-machine and m-machine flowshop scheduling problems with learning considerations[J]. Inf Sci, 2014,190:227-232. [13]WU C C, LEE W C. Single-machine and flowshop scheduling with a general learning effect model[J]. Comput Ind Eng, 2009,56(4):1553-1558. [14]ZHANG Xingong, YAN Guangle. Machine scheduling problems with a general learning effect[J]. Math Comput Model, 2010,51(1/2):84-90. [15]WANG Jibo, WANG Mingzheng. A revision of machine scheduling problems with a general learning effect[J]. Math Comput Model, 2011,53(1/2):330-336. [16]WANG Jibo, WANG Dan, WANG Liyan, et al. Single machine scheduling with exponential time-dependent learning effect and past-sequence-dependent setup times[J]. Comput Math Appl, 2009,57(1):9-16. [17]WANG Jibo, SUN Linhui, SUN Linyan. Scheduling jobs with an exponential sum-of-actual-processing-time-based learning effect[J]. Comput Math Appl, 2010,60(9):2673-2678. [18]BAI Jing, WANG Mingzheng, WANG Jibo. Single machine scheduling with a general exponential learning effect[J]. Appl Math Model, 2012,36(2):829-835. [19]CHENG T C E, LAI P J, WU C C, et al. Single-machine scheduling with sum-of-logarithm-processing-times-based learning considerations[J]. Inf Sci, 2009,179(18):3127-3135. [20]WANG Jibo, WANG Jianjun. Single machine scheduling with sum-of-logarithm-processing-times based and position based learning effects[J]. Optim Lett, 2014,8(3):971-982. [21]WANG Jibo, SUN Linhui, SUN Linyan. Single machine scheduling with exponential sum-of-logarithm-processing-times based learning effect[J]. Appl Math Model, 2010,34(10):2813-2819. [22]WANG Jibo, WANG Jianjun. Single-machine scheduling jobs with exponential learning functions[J]. Comput Ind Eng, 2011,60(4):755-759. [23]MA Haifeng, SHAO Cheng, WANG Xueru. Single machine scheduling with exponential learning functions[J]. Optim Let, 2014,8(4):1273-1285. [24]WANG Jibo, WANG Jianjun. Flowshop scheduling with a general exponential learning effect[J]. Comput Oper Res, 2014,43:292-308. [25]YANG D L, CHENG T C E, KUO W H. Scheduling with a general learning effect[J]. Int J Adv Manuf Tech, 2013,67(1/2/3/4):217-229. [26]JANIAK A, RUDEK R. A note on a makespan minimization problem with a multi-abilities learning effect[J]. Omega, 2010,38(3/4):213-217. [27]GORDON V S, STRUSEVICH V A. Single machine scheduling and due date assignment with positionally dependent processing times[J]. Eur J Oper Res, 2009,198(1):57-62. [28]ZHAO Chuanli, TANG Hengyong. A note on single machine scheduling and due date assignment with general position-dependent processing times[J]. Int J Prod Res, 2014,52(9):2807-2814. [29]RUSTOGI K, STRUSEVICH V A. Simple Matching vs Linear Assignment in Scheduling Models with Positional Effects: A Critical Review[J]. Eur J Oper Res, 2012,222(3):393-407. [30]ZHAO Chuanli, TANG Hengyong. Single machine scheduling problems with general position-dependent processing times and past-sequence-dependent delivery times[J]. J Appl Math Comput, 2014,45(1/2):259-274. [31]WANG Jibo, WANG Mingzheng. Worst-case behavior of simple sequencing rules in flow shop scheduling with general position-dependent learning effects[J]. Ann Oper Res, 2011,191(1):155-169. [32]SUN Linhui, CUI Kai, CHEN Juhong, et al. Research on permutation flow shop scheduling problems with general position-dependent learning effects[J]. Ann Oper Res, 2013,211(1):473-480. [33]RUSTOGI K, STRUSEVICH V A. Single machine scheduling with general positional deterioration and rate-modifying maintenance[J]. Omega, 2012,40(6):791-804. [34]RUSTOGI K, STRUSEVICH V A. Combining time and position dependent effects on a single machine subject to rate-modifying activities[J]. Omega, 2014,42(1):166-178. [35]ZHAO Chuanli, YIN Yunqiang, CHENG T C E, et al. Single-machine scheduling and due date assignment with rejection and position-dependent processing times[J]. J Ind Manag Optim, 2014,10(3):691-700. [36]YIN Yunqiang, XU Dehua, SUN Kaibiao, et al. Some scheduling problems with general position-dependent and time-dependent learning effects[J]. Inf Sci, 2009,179(14):2416-2425. [37]WANG Jibo, LI Junxiang. Single machine past-sequence-dependent setup times scheduling with general position-dependent and time-dependent learning effects[J]. Appl Math Model, 2011,35(3):1388-1395. [38]SHEN Lixin, WU Yubin. Single machine past-sequence-dependent delivery times scheduling with general position-dependent and time-dependent learning effects[J]. Appl Math Model, 2013,37(7):5444-5451. [39]YIN Yunqiang, WU C C, WU W H, CHEN J C, et al. Single-machine group scheduling with a general learning effect[J]. Eur J Ind Eng, 2013,7(3):350-369. [40]MOSHEIOV G. Proportionate flowshops with general position-dependent processing times[J]. Inform Process Lett, 2011,111(4):174-117. [41]MOSHEIOV G. A note: Multi-machine scheduling with general position-based deterioration to minimize total load[J]. Int J Prod Econ, 2012,135(1):523-525. [42]KUO W H, YANG D L. A short note on “Proportionate flowshops with general position-dependent processing times”[J]. Inform Process Lett, 2012,112(12):479-480. [43]GERSTL E, MOSHEIOV G. Scheduling on parallel identical machines with job-rejection and position-dependent processing times[J]. Inform Process Lett, 2012,112(3):743-747. [44]YIN Yunqiang, XU Dehua, WANG Jiayin. Some single-machine scheduling problems with past-sequence-dependent setup times and a general learning effect[J]. Int J Adv Manuf Tech, 2010,48(9/10/11/12):1123-1132. [45]WANG Jibo, WANG Jianjun. Scheduling jobs with a general learning effect model[J]. Appl Math Model, 2013,37(4):2364-2373. [46]XUE Pengfei, ZHANG Yulin, YU Xianyu. Single-machine scheduling with piece-rate maintenance and interval constrained position-dependent processing times[J]. Appl Math Comput, 2014,226:415-422. [47]LEE W C. Single-machine scheduling with past-sequence-dependent setup times and general effects of deterioration and learning[J]. Optim Lett, 2014,8(1):135-144. [48]WU C C, CHEN C J, WU W H, et al. Simulated annealing algorithms for the two-machine makespan flow shop scheduling with truncated learning consideration[J]. Int J Ind Eng, 2011,18(8):432-443. [49]WU C C, YIN Yunqiang, WU W H, et al. Some polynomial solvable single-machine scheduling problems with a truncation sum-of-processing-times based learning effect[J]. Eur J Ind Eng, 2012,6(4):441-453. [50]CHENG T C E, CHENG S R, WU W H, et al. A two-agent single-machine scheduling problem with truncated sum-of-processing-times-based learning considerations[J]. Comput Ind Eng, 2011,60(4):534-541. [51]LI Lin, YANG Shengwu, WU Yubin, et al. Single machine scheduling jobs with a truncated sum-of-processing-times-based learning effect[J]. Int J Adv Manuf Tech, 2013,67(1/2/3/4):261-267. [52]LAI K, HSU P H, TING P H, et al. A truncated sum of processing-times-based learning model for a two-machine flowshop scheduling problem[J]. Hum Factor Ergon Man, 2014,24(2):152-160. [53]WU C C, YIN Yunqiang, CHENG S R. Single-machine and two-machine flow shop scheduling problems with truncated position-based learning functions[J]. J Oper Res Soc, 2013,64:147-156. [54]LI D C, HSU P H, WU C C, et al. Two-machine flowshop scheduling with truncated learning to minimize the total completion time[J]. Comput Ind Eng, 2011,61(3):655-662. [55]CHENG T C E, WU C C, CHEN J C, et al. Two-machine flowshop scheduling with a truncated learning function to minimize the makespan[J]. Int J Prod Eco, 2013,141(1):79-86. [56]WANG Xiaoyuan, ZHOU Zhili, ZHANG Xi, et al. Several flow shop scheduling problems with truncated position-based learning effect[J]. Comput Oper Res, 2013,40(12):2906-2929. [57]WANG Xueru, WANG Jibo, JIN Jian, et al. Single machine scheduling with truncated job-dependent learning effect[J]. Optim Lett, 2014,8(2):669-677. [58]WU C C, YIN Yunqiang, CHENG S R. Some single-machine scheduling problems with a truncation learning effect[J]. Comput Ind Eng, 2011,60(4):790-795. [59]WU C C, WU W H, HSU P H, et al. A two-machine flowshop scheduling problem with a truncated sum of processing-times-based learning function[J]. Appl Math Model, 2012,36(10):5001-5014. [60]WANG Jibo, WANG Xiaoyuan, SUN Linhui, et al. Scheduling jobs with truncated exponential learning functions[J]. Optim Lett, 2013,7(8):1857-1873. Recentadvanceinschedulingwithlearningeffects ZHAOChuanli (School of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China) The concept of a learning effect on scheduling problems was first introduced by Biskup. The comprehensive survey paper on scheduling problems with learning effects was conducted by Biskup in 2008. Since then there has been an increasing interest in scheduling problems with learning effects. Therefore, besides the scheduling models mentioned in the survey of Biskup, there are several other new learning effect scheduling models in the literature. The goal of this paper was to provide a briefly review of the literature on the scheduling problems with learning effects in recent years. We mainly consider three models: 1) the actual processing time of jobs depend on specific position function; 2) the actual processing time of jobs depend on abstract position function; 3) the actual processing time of jobs depend on a truncated learning functions. scheduling; learning effects; single machine; parallel machine; flow shop 2014-09-01。 辽宁省教育厅科学技术研究项目(L2014433)。 赵传立(1958-),男,黑龙江泰来人,沈阳师范大学教授,博士,硕士研究生导师。 1673-5862(2014)04-0453-08 O223 : A 10.3969/ j.issn.1673-5862.2014.04.001

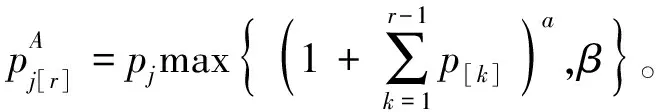


2 结 论

