基于气象地理法的舞动分布图绘制方法

李军辉，汪涛，朱宽军，张立春，黄俊杰，刘彬

(1.中国电力科学研究院，北京市102401;2.湖北省电力公司，武汉市430077)

0 引言

近年来，我国输电线路舞动事故频发，舞动影响的区域呈逐年扩大的趋势，在此背景下，绘制有效的舞动分布图从技术性和经济性方面实现差异化的防舞设计显得尤为重要［1-3］。截至目前，关于舞动分布图绘制的理论已有频率法和舞动系数法问世，舞动系数法因实际操作困难，未得到推广应用。2010年，国家电网公司出版了基于频率法的舞动分布图(一期)，该版舞动分布图完全遵循线路舞动运行经验，虽能在一定程度上反映我国电网舞动灾害分布规律，但对于缺少舞动数据或线路较少的地区来说，并不能反映真实舞动分布规律［4-8］。因此，有必要探索一套更符合实际情况的舞动区域划分理论，以指导开展舞动分布图绘制工作［9-10］。

本文通过分析线路舞动发生的要素，探讨气象、地理因子对线路舞动发生的影响规律，提出基于气象地理模型的舞动区域划分理论，据此绘制出舞动分布图，并验证其与实际情况的吻合程度［6-12］。

1 舞动气象特征

统计、分析覆冰舞动资料，是舞动分布图研究的基础，通过对大量收集的舞动资料进行甄别和归纳，找出舞动发生的时空分布特征，得到舞动时的基本气候和地域分布规律。为便于统计分析，采用同一天内造成统计地区内多处地点发生覆冰舞动，归结为同一个天气系统，成为1个覆冰舞动日。通过分析覆冰舞动日的气象特点，可以归纳出舞动发生的气象参数阈值，结合全省气象观测台(站)的气象观测数据，可以推算出全省覆冰舞动发生的概率分布，为舞动分布图的绘制奠定基础。

为确保绘制方法科学、准确，气象台(站)要覆盖全省，时间跨度越大越好，一般不少于10年，观测项目包括日平均气压、日平均气温、日最高气温、日最低气温、日平均水汽压、日平均相对湿度、日最小相对湿度、20－20时累积降水量、08－08时累积降水量、日总蒸发量、日平均风速、日照时数共12类气象资料。

天气系统背景分析的资料源于实际发生的覆冰舞动灾情资料，根据覆冰舞动日对天气系统进行归类，以找出其共同特征。气象上常用后向轨迹分析模式(hybrid single particle lagrangian integrated trajectory model，HYSPLIT)系统来对此进行分析，该系统可对待分析地区的气流轨迹进行计算并完成聚类分析，计算出的气流轨迹可以揭示待分析地区所受的主要天气系统的系统来向、系统速度、影响区域范围等特征，而聚类分析可对相似的影响系统进行合并，最终将多个影响系统合并为少数几个具有代表性的影响系统，从而利于揭示造成覆冰舞动的主要天气系统的类型及其特征。

2 舞动气象因子模型建立

2.1 单要素关系分析

通过单要素相关性分析，分析12种气象要素(气压、平均气温、最高气温、最低气温、水汽压、相对湿度、最小相对湿度、20－20时降水、蒸发、风速、日照、08－08时降水)对覆冰舞动的影响，以便找出能够简单、有效地表征覆冰舞动的气象影响因子。

2.1.1 单要素相关性分析

以某省141个覆冰舞动个例所对应的12个气象要素进行统计分析，并逐个给出不同区间段气象要素对覆冰舞动贡献的累积百分比，从而可以直观得到该种气象要素在何种区间段对覆冰舞动贡献较大。同时可以看出该气象要素在某一较集中的区间范围内对覆冰舞动是否敏感，若成立，则表示该气象要素对覆冰舞动的相关性较好。图1为12种气象要素阈值分布及其对应覆冰舞动累积百分比(各图中上面的曲线为累积百分比)。

从图1中可以看出:

(1)气压为1 010～1 020 hPa区间所占比例最大为51.4%，随着气压的递增或是递减所占比例迅速减小。导线发生舞动时，气压值大于1 010 hPa个例数占绝大多数，为总数的85.3%，而气压值大表明有冷空气侵袭，这也是导线发生覆冰舞动时所具有的环流背景。

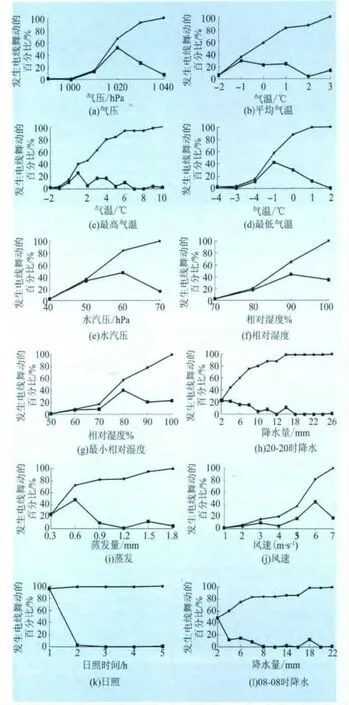
图1 12种气象要素阈值分布及其对应覆冰舞动累积百分比Fig.1 Threshold distribution of 12 meteorological factors and cumulative percentage of corresponding icing galloping

(2)平均气温变化相对不稳定。导线发生舞动时，平均气温主要集中在 －2～1℃，该区间占76.3%;在1～2℃时迅速下降，该区间所占比例仅为4%;但随着温度升高，所占比例又迅速回升，平均气温为2～3℃的区间所占比例为13.6%。

(3)最高气温的变化与导线发生舞动百分比的曲线走势呈锯齿状，没有明显的主要影响数值区间，关系对应不好。在这个区间中，以最高气温为0～1℃所占比例最大，为25.4%;比例最小的区间有2个，为6～7℃和7～8℃，当最高气温处于这2个区间时，均未发现有导线舞动现象。

(4)最低气温是三类气温(平均气温、最高气温、最低气温)中与导线舞动现象关系最为稳定，对导线舞动极为敏感的气温，最低气温为－3～1℃，占了95%以上的覆冰舞动累积百分比。在这区间中，以最低气温为－2～－1℃所占比例最大，为42.4%;比例最小区间是1～2℃，为0.6%。

(5)水汽压是表征大气中水汽含量的物理量之一，水汽压越大，大气中水汽含量越高。从百分比曲线走势上看，对应关系较好，主要集中在40～70 hPa，占了95%以上的覆冰舞动累积百分比。在这区间中，以50～60 hPa所占比例最大，为47.5%;最小区间为水汽压＜40 hPa，占2.8%。

(6)相对湿度同样也是表征大气中水汽含量的物理量之一，当大气中水汽达饱和时，相对湿度为最大值(100%)。从百分比曲线走势上看，对应关系较好，主要集中在70% ～100%，占了95%以上的覆冰舞动累积百分比，基本涵盖了所有覆冰舞动的发生概率。在这4个区间中，以80% ～90%所占比例最大，为44.1%;最小区间为相对湿度＜70%，占2.8%。

(7)最小相对湿度也是表征大气中水汽含量的物理量之一，是取每日相对湿度的最小值。从百分比曲线走势上看，对应关系较好，主要集中在60% ～100%，占了90%以上的覆冰舞动累积百分比。在这个区间中，以70% ～80%所占比例最大，为40.1%;最小区间为最小相对湿度＜50%，占1.1%。

(8)降水量取20－20时，从曲线走势上看，与导线覆冰舞动关系较弱。从区间上看，当日降水量＜2 mm时，所占比例最大，为22.6%。之后，随着降水量的增加，比例在不断下降，至12～14 mm时，已下降至0.0%。但在＞14 mm范围内，14～16 mm、24～26 mm分别占11.3%和1.1%。

(9)蒸发与导线覆冰舞动关系相对不稳定。导线发生舞动时，蒸发主要集中小于0.9 mm范围内，占81.9%;在0.9～1.2 mm迅速下降，该区间所占比例仅为1.2%，是所有区间中所占比例最小的;但随着蒸发量的增多，所占比例又有所回升，蒸发区间为1.2～1.8 mm时，所占比例为16.9%。

(10)风速取为全天的平均风速。风速因子与覆冰舞动关系较明显的区间为4～7m/s，累计百分率占80%以上。在此区间，当风速为5～6m/s时，所占比例最大，为44.6%;最小区间为风速＜1m/s，比例为1.7%。

(11)当日照时数＜1 h时，覆盖了95%以上的覆冰舞动累积百分比。表明，覆冰舞动基本上全部发生于全天日照不足1 h的情况下，说明发生覆冰舞动时，以阴雨天气为主。

(12)降水量取08－08时，从曲线走势上看，与导线覆冰舞动关系较弱。从区间上看，当日降水量＜2 mm时，所占比例最大，为48.6%。之后，随着降水量的增加，比例在不断下降，至10～12 mm时，已下降至0.0%。但在 ＞12 mm时，12～14 mm、16～18 mm、20～22 mm分别占2.3%、12.4%和1.1%。

从上面的分析可以看出，气压、最低气温、相对湿度和风速在特定区间对覆冰舞动是敏感的，表现在这4种气象要素在特定区间所对应的覆冰舞动累积百分比急剧增加并集中，说明该种气象要素在这段区间取值范围内，容易产生覆冰舞动。

2.1.2 高相关因子的选取

通过单要素相关分析，可以判断影响覆冰舞动的主要气象因子是:最低温度、相对湿度、风速。由于覆冰舞动发生的先决条件是覆冰、风速和风向，覆冰的发生与当日最低温度的相关性较好，当最低气温接近于0℃时，降水(包括可见的降水和大气中的水汽，可由相对湿度表征)可转化为覆冰，当风速和风向适合时，即可产生覆冰舞动。由于我国冬季主导风向为北风，且线路大多为南北走向，因此选取北风风向下日最大风速作为覆冰舞动模拟风速影响因子。

2.2 组合要素模型建立

通过上述的单要素相关分析，可以判断与覆冰舞动密切相关的几个气象因子分别是:日最低温度、日平均相对湿度、日最大风速和日最大风速对应的风向。对某省141个覆冰舞动个例进行分析，得到舞动气象阈值区间为:日最大风速所对应的风向为北风(包括东北风、西北风等偏北的风向);最大风速区间为4～15m/s，最低气温区间为－5～3℃，日平均相对湿度≥70%，该条件覆盖所有141个覆冰舞动个例，占总个例的100%。

2.3 台站历史序列重建

通过上述气象要素模型，对某省全部78个观测台(站)1998—2010年每年的11月至次年3月的逐日历史资料进行回算，统计78个台(站)13年的覆冰舞动总次数，并折算为年频次后进行10年总次数的分布图绘制，见图2所示。

3 地形修订

3.1 地理因子识别

覆冰舞动与局部地形的关系较为复杂。较为普遍的认识是:平原地区覆冰舞动多发、丘陵地区次之，山区少见，且与海拔高度的相关性不明显，但丘陵和山区中的平原(微地形)线路仍然会发生舞动，从调研中也反映出这种规律。针对这些因素，重点考虑的是可否找出一个指标来表征一定范围内的地势是否较为平坦，从而区分平原、丘陵和山区地形。

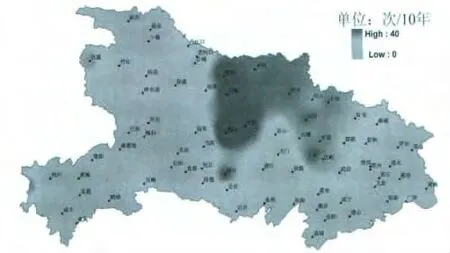
图2 某省舞动频次分布图(气象模型)Fig.2 Distribution of galloping frequency for a province(meteorological model)

在常用的地理规范数据中，一般用海拔高度、坡度、坡向来表征地形。对于海拔高度，其仅能代表某一点的海拔信息，无法表征其周围点的相对高低状况，故无法成为表征地形的指标;对于坡向，其代表某一点坡面的朝向，也无法表征其周围点的相对高低状况，故也无法成为表征地形的指标;对于坡度，其数值的大小，代表该点地形起伏的程度，坡度越大，表明该点越陡峭，坡度越小，表明该点越平坦，故坡度可以代表该点的地形。

但若选择坡度作为地理识别因子，存在一个不可回避的问题，即坡度仅能代表当前点的地形特征，无法表征某一区域内的地形是属于平原抑或山区。这个问题可以通过降低地形资料的精度来获得较粗格网(相当于增加了坡度计算的范围)的坡度信息来解决，但会影响到实际需求的精度。最终，选定使用地形起伏度作为这个指标。

地形起伏度是指指定范围内最大相对高程差，它是描述某个区域地形特征的一个宏观性的指标，从其定义中可以看出，地形起伏度的实质仍是坡度概念的延伸。地形起伏度最早源于前苏联科学院地理所提出的地形切割深度，现在成为划分地貌类型的一个重要指标。

由于海拔高度、坡度和坡向均无法反映一定范围内地形起伏的规律，造成无法标识出特定范围内的地形特征是属于平原、山地或丘陵，而地形起伏度计算半径可调这个特点决定了其实际应用时的便利性，同时该参数也能很好地表征其计算半径范围内的地形特征。

不同的地形起伏度计算半径所描述的地势情况是不同的，因此，需要确定出合理的计算半径以清晰地显示出平原、丘陵、山地这3种地形。表1是某省不同计算半径下3种地形起伏度分布情况。

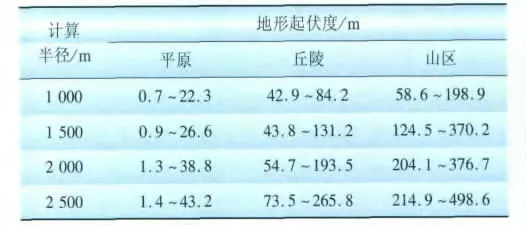
表1 不同计算半径下3种地形起伏度分布Tab.1 Distribution of 3 topographic prominences at different radius for calculation

从表1的统计数据可以看出，2 000m左右的计算半径是较为合适的，在这个半径范围内，3种地形没有明显的地形起伏度重叠，而另外3种计算半径范围内，3种地形的地形起伏度重叠均较为明显，尤其是丘陵和山区不能有效分开，故选定2 000m半径为地形起伏度计算半径。图3是某省地形起伏度分布计算图。

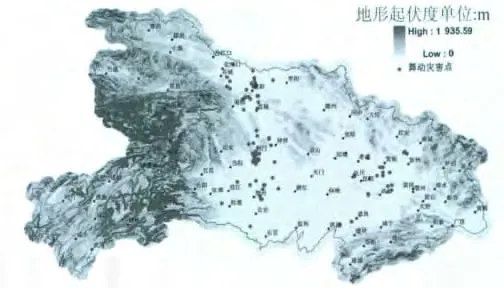
图3 某省地形起伏度分布图Fig.3 Distribution of topographic prominence for a province

结合实际覆冰舞动灾害点分布可见，覆冰舞动灾害点基本分布于地形起伏度较小的地区。可见线路覆冰舞动与其所在局部的地形平坦程度，亦即地形起伏度的关系更为密切。

3.2 定量订正关系建立

3.2.1 定量关系建立方法

在2 000m起伏度计算半径条件下，通过建立78个观测台(站)地形起伏度与其对应舞动总次数的数学关系模型，可定量地对全省范围内的覆冰舞动总次数进行推算。

3.2.2 定量关系计算结果

以某省为例，建立全部气象台(站)的覆冰舞动总次数与其地形起伏度的数学模型关系，二者的散点关系图和模型如图4所示。当地形起伏度小于100m时，地形起伏度与舞动总次数没有明显的关系，当起伏度逐渐增加时，覆冰舞动次数随之减小的趋势越来越明显，故可以考虑不对地形起伏度小于100m的区域做订正，仅对地形起伏度大于100m的区域做出定量订正。

图4 覆冰舞动总次数与地形起伏度散点图Fig.4 Scatter diagram of total frequency of icing galloping and topographic prominence

图5 给出了当地形起伏度大于100m时与覆冰舞动次数的关系，可以看出这种关系明显好转。采用对数关系模型，其复相关系数可达0.233 6，即相关系数为0.483。从模型可见，地形起伏度越大，覆冰舞动总次数越小，当地形起伏度达到约700m时，覆冰舞动总次数基本为0。故在实际计算中，当覆冰舞动次数计算值为负时，将其归0，认为不会发生覆冰舞动，这也说明山区发生舞动的可能性小的原因。

图5 覆冰舞动总次数与地形起伏度(大于100m)散点图Fig.5 Scatter diagram of total frequency of icing galloping and topographic prominence(＞100m)

最终确定对全省覆冰舞动总次数进行地形订正时，当地形起伏度小于100m，直接使用气象因子建模的插值结果;当地形起伏度大于100m，使用如下指数关系模型进行计算:

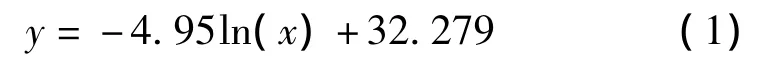
式中:y为覆冰舞动总次数;x为该点的地形起伏度。

4 气象地理法建模

4.1 模型建立流程

具体分步流程为:

(1)应用HYSPLIT分析覆冰舞动发生的天气背景，从而确定覆冰舞动发生的主要天气类型，最终得到本地区发生覆冰舞动时的主导气流来向;

(2)统计本地区覆冰舞动个例发生时所对应的三大气象要素阈值分布，三大气象要素分别是日最低气温、日相对湿度和日最大风速(含风向);

(3)获得该区域所有气象观测台(站)冬季(以及初春)逐日四要素气象资料(日最低气温、日相对湿度、日最大风速和日最大风速对应的风向)，根据前面的阈值分布特征对台(站)覆冰舞动历史序列进行重建，以完成覆冰舞动的气象要素建模模拟流程;

(4)获取本地区的数字高程(digital elevation model，DEM)资料，并计算2 000m计算半径下的地形起伏度。根据实际覆冰舞动灾害点的地形标识(平原、丘陵、山区)进行验证;

(5)读取本地区气象台(站)点的地形起伏度数值，并与历史重建的覆冰舞动总次数进行相关分析，建立二者的定量关系;

(6)利用美国Arc地理信息系统软件(Arc geographic information system，ArcGIS)的格点计算功能，在本地区地形起伏度格点资料的基础上，利用建立的公式，对本地区的覆冰舞动进行计算，从而得到高精度的覆冰舞动总次数估算数据。

4.2 模型计算结果

利用地形影响因子所建立的定量订正的指数关系式，对全省覆冰舞动总次数进行模拟，当地形起伏度小于100m时，直接使用气象因子建模的插值结果。当地形起伏度大于100m时，使用指数关系模型进行计算，模拟结果如图6所示。

图6 某省覆冰舞动频次分布图(气象地理法模型)Fig.6 Frequency distribution of icing galloping for a province(meteorological-geographical method model)

从图6可以看出，绘制结果与舞动的灾情实况基本吻合。

5 舞动分布图分级

5.1 分区分级的依据

为了将覆冰舞动分为不同的等级，需要对其进行分区分级。数学方法中，常用的客观分区分级方法有很多种，在灾害评估方面，较常用的方法有百分位法及重现期法(其数学实现是利用耿贝尔极值Ⅰ型分布型)，由于覆冰舞动有多个台(站)的多年历史拟合序列，根据其数学特征，利用百分位法对结果进行分区分级较为合理。

百分位数是一种位置指标，常用于描述一组样本值在某百分位置上的水平，用PX来表示，一个百分位数PX将全部变量值分为2个部分，在PX处若无相同变量值，则在不包含PX的全部变量值中有X%的变量值小于它，(100－X)%变量值大于它，当X%=50%时PX即对应中位数。多个百分位结合使用，可更全面地描述资料的分布特征，常用于分级或制定评定标准。百分位数法在各个行业均有应用，尤其是在医学、体育、气象等方面应用较广。

百分位数法的计算采用Hyndman R.等［13］推荐的方法，此方法也是统计产品与服务解决方案软件(statistical product and service solutions，SPSS)［14］采用的方法，计算公式为

5.2 分区分级标准研究

根据经验，覆冰舞动区域的分区分级定位4级，分别是非覆冰舞动区、轻度覆冰舞动区、中度覆冰舞动区和重度覆冰舞动区。将某省覆冰舞动总次数利用百分位法进行级别划分，当给定的百分位为0.3、0.6、0.9时，可得相对应的覆冰舞动总次数截断点分别是1.4、6.2、23.4次，利用这个截断点可将某省覆冰舞动总次数划分为要求的4个等级，如图7所示。

图7 分级后某省舞动分布图Fig.7 Icing galloping distribution for a province after classification

根据运行经验，该省电力系统舞动分布图与理论分析一致，也与实际相符，充分证明应用气象地理法得出的结果是科学合理的。

6 结论

(1)继频率法、舞动系数法之后，本文提出了基于气象地理法的输电线路舞动分布图绘制方法。气象地理法不考虑实际输电线路影响，以容易获取的气象、地理数据为基础，通过总结气象、地形特征规律，建立覆冰舞动的气象模型和地理模型，从而成为一套更符合实际情况的舞动分布图绘制方法。

(2)通过气象模型计算出符合舞动条件的舞动气象日数，绘制出基于气象模型舞动日数分布图，并采用地形起伏度修订模型对舞动气象日数分布图进行修订，绘制出基于气象地理模型的舞动日数分布图，最后采用百分位法对舞动分布图进行区域分级，完成舞动分布图绘制。本文方法可指导开展舞动分布图绘制工作。

(3)以某省为例采用气象地理法绘制了舞动分布图，通过运行经验检验，与实际舞动情况较为吻合，说明该方法是合理、可靠的。

［1］郭应龙，李国兴，尤传永.输电线路舞动［M］.北京:中国电力出版社，2003:1-20.

［2］Rawlins G R.Research on vibration of overhead ground wires［J］.IEEE Trans.on Power Delivery，1988，3(2):769-775.

［3］Gupta S，Wipf T.Structural failure analysis of 345kV transmission line［J］.IEEE Trans.on Power Delivery，1994，9(2):894-903.

［4］Tsujimoto K，Iisaka H，Shimojima K，et al.Report on experimental observation of galloping behaviour in 8-bundled conductors［J］.IEEE Trans.on Power Apparatus and Systems，1983，102(5):1193-1201.

［5］Parkinson G V，Smith J D.The square prism as an aeroelastic nonlinear oscillator［J］.The Quarterly Journal of Mechanics and Applied Mathematics，1964，17(2):225-239.

［6］马建国.湖北省电网导线舞动区域划分［J］.电力建设，1999，20(5):39-40.

［7］王少华，蒋兴良，孙才新.输电线路导线舞动的国内外研究现状［J］.高电压技术，2005，31(10):11-14.

［8］赵作利.输电线路导线舞动及其防治［J］.高电压技术，2004，30(2):57-58.

［9］朱宽军，刘超群，任西春，等.特高压输电线路防舞动研究［J］.高电压技术，2007，33(11):61-65.

［10］丁锡广，陶文秋.减轻送电线路导线舞动灾害的措施［J］.高电压技术，2004，30(2):54-55.

［11］尤传永，卢明良.架空输电线路导线舞动的防止措施［J］.中国电力，1993(8):41-43.

［12］黄经亚.架空送电线路导线舞动的分析研究［J］.中国电力，1995，28(2):21-26.

［13］罗纳德.D.约克奇.SPSS其实很简单［M］.刘超，吴铮，译.北京:中国人民大学出版社，2010.

［14］骆方，刘红云，黄昆.SPSS数据统计与分析［M］.北京:清华大学出版社，2011.