基于改进最优覆盖法的智能变电站无功优化配置

段国泉，戚庆茹，吴军，刘涤尘，柯丽娜，祁林阁

(1.武汉大学电气工程学院，武汉市430072;2.国网北京经济技术研究院，北京市102209)

0 引言

智能电网是未来电网发展方向，涵盖发电、输电、变电、配电、用电、调度、通信信息等各个环节。其中智能变电站是智能电网的基础，是整个电网安全、可靠运行的重要环节［1-2］。智能电网对电能质量、线损及电压稳定提出了更高的要求，要求智能变电站的无功能实现实时就地控制。采用单一的电容器分组补偿略显乏力，不能实现无功的实时就地平衡原则;而完全配置动态无功补偿装置初期投资大，也不符合经济性原则，故需要考虑将电容器与动态无功补偿装置共同配置于变电站并进行协调优化。但目前关于电容器与动态无功补偿装置协调优化配置的研究还不多见［3-4］。

变电站的无功优化配置是优化规划类问题，不同于优化控制问题，主要研究无功补偿装置的配置位置、类型、容量的确定，而不需要考虑补偿装置的实时响应控制等问题。目前通常研究的是补偿点的确定、电容器分组优化及总容量的确定问题。文献［5－6］利用电压稳定性及灵敏度分析来确定补偿点的位置，文献［7－9］将优化配置问题中的投资及有功损耗统一为经济最优问题，并辅以电网安全的约束，采用优化的方法进行处理。文献［10－12］提出一种电容器等容优化分组方法，根据变电站全年无功负荷统计出无功概率分布曲线，采用最优覆盖思想建立电容器组优化分组模型，并通过全局搜索进行寻优。

以上方法均只考虑单一补偿类型，未将动态无功补偿装置与电容器相配合进行研究考虑。本文立足于智能变电站，研究动态无功补偿装置与电容器的协调配置问题，并对文献［11］中的最优覆盖法进行改进使之适用于2种补偿装备的协调配置，在不考虑具体时间点的实时补偿情况下，基于全年的无功负荷情况进行概率上的无功配置计算。因静止无功补偿器(static var compensator，SVC)技术成熟，成本相对较低，故采用SVC与电容器组共同配置，在分析等容及几种典型不等容分组情况下，对概率曲线进行覆盖，以达到更优的补偿效果，并构造基于最优覆盖的目标函数与投资成本函数的多目标优化数学模型，最后采用遗传算法对目标函数进行寻优，得到等容与不等容的几种不同优化配置方案，从中选取最优方案［13］。

1 最优覆盖法的改进

传统最优覆盖法中，力求解决的是电容器等容分组的问题，关键在于利用无功概率分布曲线建立未覆盖面积(即失配面积)最小的目标函数，以及利用全局搜索获得优化配置方案。其中全局搜索是通过搜索工程上每一个可选电容器组容量对应的失配面积，逐一对比获取最小值，且采用全局搜索可不需要考虑概率曲线具体函数。

而对智能变电站进行无功优化配置时，将SVC引入最优覆盖法中，其容量为从0到最大容量的可变连续值，与补偿容量为离散值的电容器共同覆盖概率曲线。由于电容器组为离散变量，补偿投切时的概率覆盖曲线为台阶状的，电容器不同组间有极差而不能对概率分布曲线完全覆盖，由此形成失配面积。在此基础上配置SVC，对因电容器组极差而产生与概率分布曲线失配的面积进行二次覆盖。因为SVC属于动态无功补偿，能动态无级连续补偿，其补偿的量为连续值，能跟踪概率分布曲线进行补偿，所以能极大优化失配面积。

在考虑协调配置情况的同时，讨论SVC与电容器组等容及不等容2种分组方式的配合情况。等容分组沿用传统最优覆盖思想;不等容分组方式在传统覆盖方法上进行适应性修改，最小分组即为阶梯补偿极差，容量组合数取代分组数作为面积覆盖中的级数，并考虑不等容分组频繁投切造成的设备损耗加剧情况，从而获得不等容分组的配置模型。

因加入连续变量且考虑等容与不等容2种分组方式，所以需要对该思想进行4个方面的改进。

(1)加入连续变量SVC容量后必将导致在SVC取尽可能大后，无论电容器组如何取值，目标函数均收敛于0。故可增加一个投资成本函数与失配面积函数构成一个多目标优化问题。

(2)进行不等容分组方式讨论时，对覆盖面积函数及成本函数进行适应性修改。因不等容分组造成操作更频繁，设备损耗更大，而运行复杂度难以转换为经济量进行定量分析，而操作造成的损耗加剧可在目标函数中加入设备折损系数定量确定。

(3)需要对概率分布曲线进行处理。通过matlab软件对由离散点生成的概率曲线进行拟合，生成具体的函数表达式。

(4)最普通全局寻优不能适用多目标优化问题，本文将采用经典遗传算法进行计算分析。

2 等容分组与SVC协调配置的数学模型

改进型最优覆盖法具体实施思路为通过往年无功负荷曲线，生成变电站的无功负荷概率分布曲线，配置电容器组及SVC进行无功补偿，对无功概率曲线进行覆盖，其中未覆盖面积为无功失配面积，通过配置不同电容器单组容量及分组，并且利用SVC对电容器组欠补偿部分进行优化覆盖，达到无功失配面积最小，即为最优覆盖。本文在原最优覆盖基础上加入SVC进行协调补偿，以期得到更优化的配置方案。

2.1 进行数据分析，生成概率曲线与分布函数

通过变电站实测系统采集全年无功负荷数据，利用概率分布曲线原理将负荷数据生成概率分布曲线:生成前，进行数据过滤，滤去异常数据;生成过程，从0开始，增加一个ΔQ的增量，每一次增加后，统计大于该容量的数据点数，然后除以总点数得到该点的概率，直至增加到该变电站的最大无功负荷停止，由此得到大量离散的无功概率分布点，将这些离散的点绘制成一条连续曲线。

最后通过matlab进行曲线拟合，由离散点生成具体的无功负荷概率分布函数F(Q)。由此方法得到的变电站典型无功负荷分布曲线如图1所示。

图1 典型无功负荷概率分布曲线Fig.1 Probability distribution curve of typical reactive load

2.2 无功失配面积最小的目标函数

生成无功负荷概率曲线后，进行无功补偿装置的最优覆盖。其中电容器组无功负荷的覆盖为阶梯形的覆盖面积S1，由于SVC为柔性补偿特性，能动态无极差补偿无功，故在电容器阶梯补偿的基础上，可沿曲线边界进行二次补偿，覆盖电容器组因极差造成的失配面积。由此可得电容器组和SVC共同覆盖概率曲线，示意图如图2所示。

图2 改进最优覆盖法示意图Fig.2 Improved optimal cover method

对图中曲线内未被补偿装置覆盖到的所有空白失配面积进行积分后相加，即可得到无功失配面积的目标函数。

因此无功失配面积的目标函数可描述为

式中:M为电容器组数;QM为电容器单组容量;QC2为SVC的容量。

2.3 投资成本最优的目标函数

电容器组的投资成本一般包括2个部分:每组配套设施投资及电容器成本。其中配套设施成本包括:断路器成本、隔离开关成本、占地费用、运行维护费用及相关其他设备费用;电容器成本则与其容量成正比。

由此可得并联电容器组的投资成本为

式中:M为并联电容器分组数;QC1为电容器总容量;c1为每组电容器配套成本;c2为电容器的单价。

对于动态无功补偿设备，其单价较贵，可以认为其成本为容量的线性函数:

式中c3为SVC的单价。

所以装设了电容器组与SVC的智能变电站的总投资成本目标函数可以统一写作:

2.4 多目标数学模型的建立

考虑失配面积最小及投资成本最小2方面的模型可描述为

式中:f1为无功失配面积;f2为投资总成本。约束条件为电容器分组、总补偿容量、电容器组单组容量及SVC容量的上下限。

2.5 多目标问题的处理

进行优化计算前，对多目标优化问题进行处理，通过统一2个目标函数纲量，将多目标函数转化为单一目标。对于投资成本函数，利用等年值法，把折算系数加入投资成本中，折算为设备年运行损耗费用;对于最优覆盖法生成的失配面积最小目标函数，乘以年运行时间，并引入无功损耗电价，将无功失配量转化为年无功损耗费用;最后将两者线性相加获得最终的单一目标函数，并定义为年损耗费用:

年运行损耗费用:将前式中无功失配面积最小的目标函数，乘以年运行时间T及无功损耗电价τ，即得年无功损耗费用:

年设备损耗费用:利用等年值法，将投资成本乘以折算系数转化为年运行损耗费用，其中r为贴现率，m为设备的使用年限。处理后所得目标函数为

最后定义年损耗费用:年损耗费用为上述年无功损耗费用与年运行损耗费用的线性相加。则无功配置的目标函数最终表现为年损耗费用:

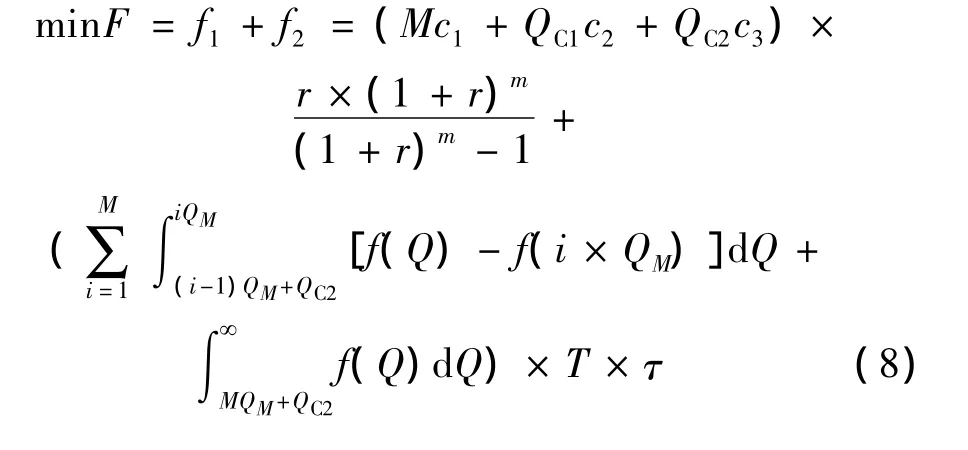
3 不等容分组的优化配置模型

不等容分组是将电容器按照不同比例进行分组，以期用较少的分组数获得较多的组合情况，主要方式有等比、等差及不均匀分组。其中典型的不均匀分组由研究可知有:(1)将一部分电容器分为大组，另一部分电容器分为小组，大组容量可为小组的2倍(1∶1∶2∶2，1∶1∶1∶2∶2∶2);(2)将电容器分为 1 个大组及若干小组，其中所有小组容量之和为大组容量(1∶1∶2，1∶1∶2∶4，1∶2∶3∶6)。

以分4组为例，几种典型不等容分组方式如表1所示。

表1 典型不等容分组方式Tab.1 Typical unequal capacity grouping method

通过组合，等比分组可得15种容量组合;等差分组可得10种容量组合;不均匀分组(a)可得6种容量组合;不均匀分组(b)可得8种容量组合;而若采用等容分组(1∶1∶1∶1)则只有4种容量组合。

在讨论应用最优覆盖法解决不等容分组的电容器组与SVC协调配置时，采用前文的数学模型，进行如下适应性修改。

(1)失配面积函数的修改。因不等容分组投切的极差为最小单组容量，所以在式(1)中，用最小单组容量QM1代替等容的单组容量QM，此时式中分组数M变为容量的组合数MZ。因此式(1)修改为

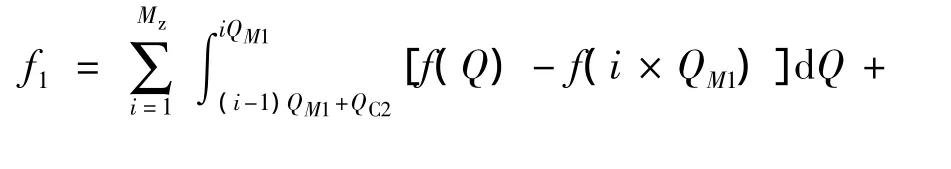
(2)年损耗费用的修改:考虑不等容情况下设备折损的加剧。在相同分组下，不等容分组相比等容分组，组合容量更多，投切更为频繁，因而造成设备损耗也更为加剧。所以在考虑年设备损耗费用时，引入不等容分组的折损系数λ，定义为组合容量数与分组数的比值，因此等容分组下折损系数λ=1，不等容分组依情况而定。如等差分组(1∶2∶3∶4)的折损系数λ为组合数10与分组数4的比值，即为2.5。

在加入折损系数后，等容及不等容分组的目标函数可统一为(其中等容分组中mZ=M，QM1=QM，λ =1)

4 算例分析

取某个110kV变电站的全年无功负荷进行统计计算，数据源是该变电站1年的电网实时监测数据，如图3所示。

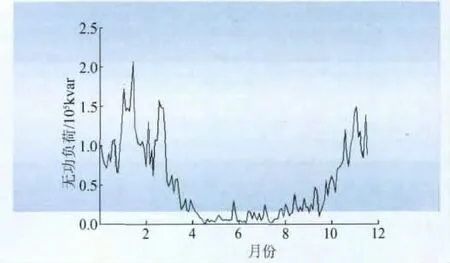
图3 变电站全年无功负荷Fig.3 Annual reactive load of substation

进行数据分析，生成概率分布曲线，并进行曲线拟合，在matlab界面生成拟合曲线图，如图4所示。

该变电站有2台主变，每台容量为50 MVA，原电容器组配置为4×4 Mvar。根据变电站容量等相关指标得到约束条件的上下限及工程实际中各种参数数值如表2与表3所示。

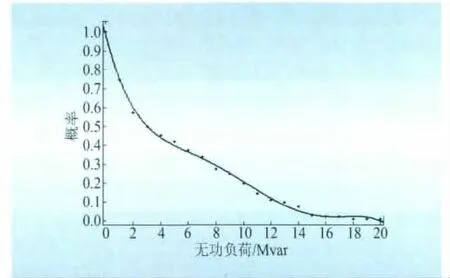
图4 无功概率分布与拟合情况曲线Fig.4 Reactive power probability distribution and fitting curve

表2 成本参数Tab.2 Cost parameters

表3 约束条件Tab.3 Constraint conditions

利用遗传算法进行计算时，初始种群大小取100，交叉概率取0.85，变异概率取0.15，最大迭代代数取500。因原配置方案分4组，不等容分组的分组数不大于4组，且避免组合过多造成操作运行复杂，组合数选取不大于10组。故选取的4组典型不等容分组为:1∶2∶3，1∶2∶4，1∶1∶2∶2，1∶1∶2∶4。

最后所得配置方案如表4所示。结果对比如表5所示。

由优化结果可知:

(1)通过改进最优覆盖法获得的“等容分组+SVC”与“不等容分组+SVC”的优化配置方案与原方案对比，虽然前期投资有所提高，但象征补偿效果的失配系数更低，补偿效果更佳，且年损耗费用大幅下降，综合经济效应更优。

(2)等容分组方案相比不等容方案前期投资更高，但考虑折损情况及补偿效果下，综合经济指标年损耗费用更低，故该变电站适宜采用“等容分组电容器+SVC”的配置方案。

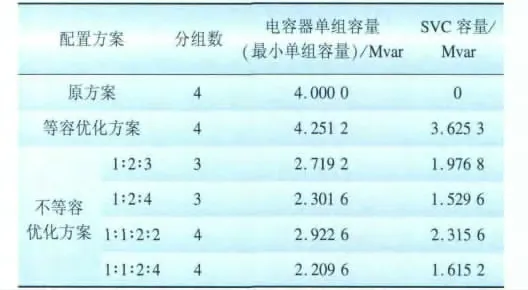
表4 配置方案Tab.4 Configuration schemes

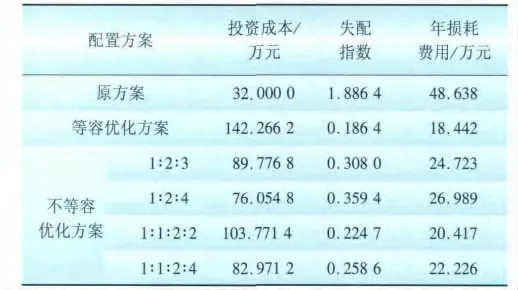
表5 配置方案的对比Tab.5 Comparison of configuration schemes

5 结语

对智能变电站无功进行优化配置可有效减少无功层间流动，降低系统网损，为实现坚强智能电网打牢基石。本文在传统电容器组补偿基础上加入SVC进行协调补偿，建立了基于改进最优覆盖思想的多目标优化模型，并采用遗传算法对实际变电站进行优化计算，优化后结果与原有配置方案对比，有效降低了年损耗费用，并对系统有更好的补偿效果。该优化方法解决了电容器组与SVC的联合配置问题，从概率的角度处理问题，避免了从单一时间点考虑问题时，无功负荷情况的片面性;且只需要了解前年负荷情况即可进行优化计算，具有可操作性;同时可以对日后智能变电站的无功配置提示指导性建议，例如通过算例分析可知，对于110kV智能变电站，可采用以电容器为主，SVC为辅，且由本方法可确定具体容量。

随着性能更为优良的其他无功补偿装置的发展与智能变电站的推广建设，可进一步研究多种动态无功补偿的协调配置及面对其他复杂负荷如微电网接入情况时的配置情况。

［1］田成凤.智能变电站相关技术研究及应用［D］.天津:天津大学，2010.

［2］李瑞生，李燕斌，周逢权.智能变电站功能架构及设计原则［J］.电力系统保护与控制，2010，38(21):47-48.

［3］ResearchReports International.Understanding the smartgrid［R］.Research Reports International，2007.

［4］黄安平.智能电网下电压优化协调控制研究［D］.广州:华南理工大学，2011.

［5］姚小寅，孙元章，王志芳.电力系统无功源最佳配置地点的研究［J］.电力系统自动化，1999，23(3):12-15.

［6］胡彩娥，杨仁刚.考虑电压稳定的电力系统无功优化规划［J］.继电器，2005，33(4):22-25.

［7］刘科研，盛万兴，李运华.基于改进免疫遗传算法的无功优化［J］.电网技术，2007，31(13):11-16.

［8］刘方，颜伟，Yu D C.基于遗传算法和内点法的无功优化混合策略［J］.中国电机工程学报，2005，25(15):67-72.

［9］李亚男，张粒子，舒隽，等.结合专家知识的遗传算法在无功规划优化中的应用［J］.电网技术，2001，25(7):14-17.

［10］王佳贤，程浩忠，胡泽春.多负荷水平下的配电网无功优化规划方法［J］.电网技术，2008，32(19):56-61.

［11］王一杰.无功优化实用化研究［D］.杭州:浙江大学，2011.

［12］刘燕.中低压配网无功补偿优化配置研究［D］.南京:南京理工大学，2009.

［13］胡泽春，钟明明，王佳贤，等.考虑多负荷水平的中低压配电网无功补偿优化规划［J］.电工技术学报，2010，25(8):167-173.