时变领航情况下多智能体网络一致性分析与应用

于 镝，李 铖，冷传英，任伟建

（1.东北石油大学 电气信息工程学院，黑龙江 大庆 163318； 2.大庆石化公司 热电厂，黑龙江 大庆 163714）

0 引言

近年来，多智能体协调控制作为复杂系统和控制科学领域的前沿课题被人们关注，并且在航空航天、军事、民用等方面得到广泛应用［1-3］.作为多智能体协调控制的基本问题，一致性问题在多机器人编队［4］、群集［5-6］、任务分配［7］和传感器网络定位［8］等方面起重要作用，目的是通过设计分布式控制协议，使多智能体网络中每个智能体的最终状态趋于一致［9-10］.

人们对个体动态为一阶积分器的多智能体网络进行研究［11-16］.Jadbabaie A等基于最近邻规则设计简单的控制协议，采用非负矩阵理论讨论无向固定网络拓扑和切换网络拓扑情况下的一致性问题，给出网络实现一致的充分条件［11］.在Jadbabaie A等研究基础上，Olfati-Saber R等给出整个多智能体网络的控制框架，将网络一致性和控制系统稳定性联系起来，分别讨论无向图、有向平衡图情况下网络的一致性和平均一致性问题［12］.这些研究为多智能体网络一致性分析和控制奠定理论基础.Ren W等进一步讨论有向拓扑网络的一致性，应用矩阵理论给出最终一致解［13］，并在Jadbabaie A等结论基础上，研究有向切换拓扑网络的一致性［14］，拓宽对网络拓扑的限制.Moreau L基于凸论和设定值Lyapunov理论研究多智能体网络的稳定性问题［15］.Lin Z等为一组移动智能体无向拓扑情况下的编队问题提出3种不同控制方案，最终目标是静态点［16］.王垚等研究智能体网络的量化一致性问题［17］.

目前研究多为考虑无领航或领航者状态恒定的情况，实际应用中，为了更快速有效地完成协调任务，在多智能体网络中通常存在状态时变的领航智能体.当协调目标为时变参考轨迹时，即网络存在虚拟领航者，如在进行多车辆或多机器人编队控制时，编队中心的时变轨迹即为整个多智能体网络的虚拟领航者.由于存在通信范围和带宽的限制，网络中仅有部分个体能够获取领航者的状态信息，因此在部分个体已知时变领航者状态的情况下，有向拓扑网络一致性问题的研究尤为重要.

笔者对时变领航情况下多智能体网络进行一致性分析.首先，设计领航状态信息为时变情况下的一致性控制算法，实现部分智能体已知领航状态信息情况下的一致性追踪，给出实现一致的充要条件及算法；然后，将此算法拓展至个体与领航者之间存在状态偏差情况，提出基于偏差情况下的分布式控制算法，给出保持恒定偏差的充要条件及算法；最后，应用编队仿真实验验证基于2种情况算法的控制协议的正确性.

1 理论基础和问题描述

1.1 基于图论的多智能体网络的拓扑关系

网络中智能体间的信息交换可用有向或无向图G加以描述.首先令λn＝｛1，2，…，n｝代表指标集，图G＝（V，E）由节点集V（G）＝｛vi，i∈λn｝和边集E（G）⊆｛（vi，vj）：i，j∈λn｝构成.若（vi，vj）是图G 的一个边，那么vi称为父节点，vj称为子节点.在无向图中边均为无向，即节点vi和节点vj能够互相获取信息.有向图是由一系列有序的边（vi1，vi2），（vi2，vi3），…，（vi2n，vin＋1）构成，其中vij∈V（G）.若边（vi，vj）存在，表示节点vj能够获取节点vi的信息，则邻接矩阵元素aij＞0；否则，aij＝0，∀i，j∈λn.网络中智能体之间的拓扑关系用Laplacian矩阵L＝［lij］∈Rn×n表示，其中

1.2 问题描述

考虑由n＋1个智能体所构成的有向网络，其中第i个跟随智能体的动态表示为

式中：xi为第i个智能体的状态，xi∈Rn；xi（0）为第i个智能体的初始状态；ui为第i个智能体的控制输入，ui∈Rn.

为不失一般性，令领航者为第n＋1个智能体的状态为xn＋1＝xr，动态为

式中：xr为领航者的状态，xr∈Rn；f为非线性函数.

针对多智能体网络，在只有部分智能体已知领航时变状态xr（t）的情况下，基于邻居信息设计控制协议ui，使多智能体网络能够渐近达成一致.主要考虑2种情况：

定义1 若对于任意的xi（0），i＝1，…，n，当t→∞时，有xi（t）→xr（t），则称该智能体网络实现渐近跟踪一致.

定义2 若对于任意的xi（0），i＝1，…，n，当t→∞时，有xi（t）→xr（t）＋其中为第i个智能体与领航者之间的期望状态偏差，则称该智能体网络实现相对状态保持期望偏差的渐进一致.

引理1［13］假设网络状态矢量x＝［x1，x2，…，xp］T，xi∈R，L∈Rp×p满足 Laplacian矩阵性质，情况等价：（1）L有一个和特征向量lp相对应的简单0特征值，其他所有特征值存在正实部；（2）Lx＝0意味着x1＝x2＝…＝xn；（3）系统˙x＝-Lx渐进趋于一致；（4）L的有向图存在一个有向生成树.

2 一致性跟踪分析算法

考虑仅有部分智能体在已知时变领航状态xr情况下，多智能体网络（1）的跟踪一致性问题.基于邻居相对信息，提出一致性算法：

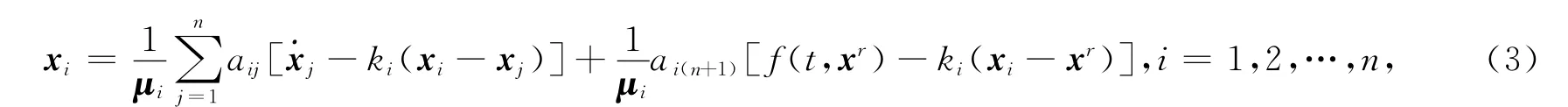
式中：ki为控制增益参数当智能体vi可以收到领航者的状态信息时，ai（n＋1）＞0；否则，ai（n＋1）＝0.

定理1 考虑多智能体网络（1），当且仅当网络拓扑具有有向生成树时，采用控制协议（3），可实现网络的跟踪一致.

证明：先证充分条件.当网络拓扑具有有向生成树时，由引理1可得-Ln＋1x＝0，则xi＝xj＝xn＋1≡xr，i，j＝1，2，…，n，即网络实现渐近跟踪一致.

再证必要条件.将控制协议（3）带入网络动态（1），可得

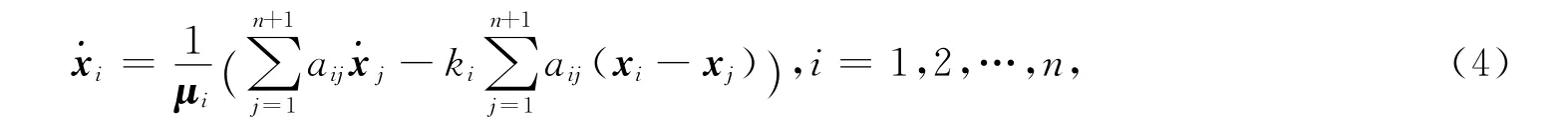
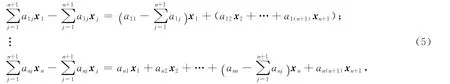
所以-Ln＋1x→0，其中网络状态矢量为包含领航者在内的n＋1个智能体所构成网络的Laplacian矩阵

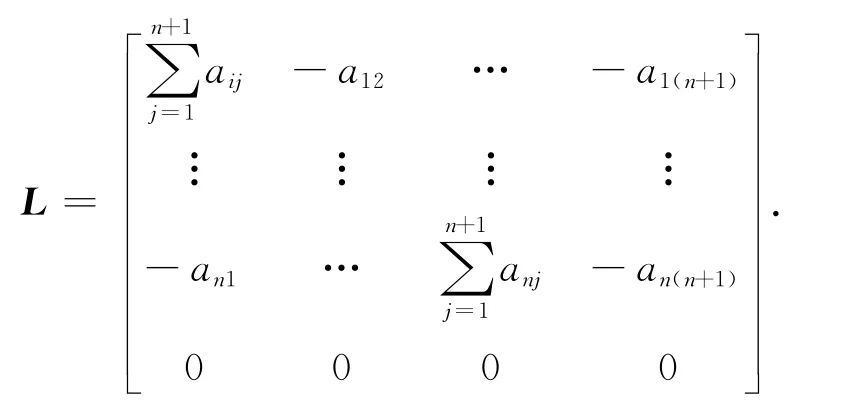
由引理1可得xi→xr，i＝1，2，…，n，即网络实现跟踪一致，并且网络拓扑具有有向生成树.

3 相对状态保持期望偏差的渐近一致性分析

在实际应用中，当考虑跟随智能体与领航智能体之间存在恒定距离时，需要考虑相对状态保持期望偏差的渐近一致问题.此时将算法（2）进一步拓展，提出一致性算法：

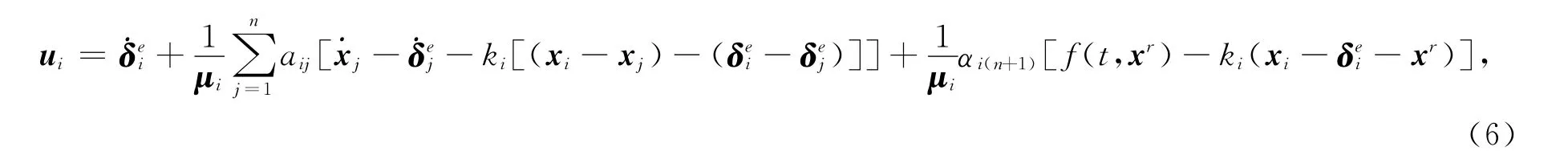
定理2 考虑多智能体网络（1），当且仅当网络拓扑具有有向生成树时，采用控制协议（6），可实现相对状态保持期望偏差的渐近一致.

先证明充分条件.当网络拓扑具有有向生成树时，由引理1可得＝1，2，…，n；因为即网络实现相对状态保持期望偏差的渐近一致.

再证明必要条件.由于式（7）形同于协议（3），根据算法（3）必要条件的证明过程，由定理1可得→xr，i＝1，2，…，n时，网络拓扑具有有向生成树，即当网络拓扑具有有向生成树.

4 仿真实验

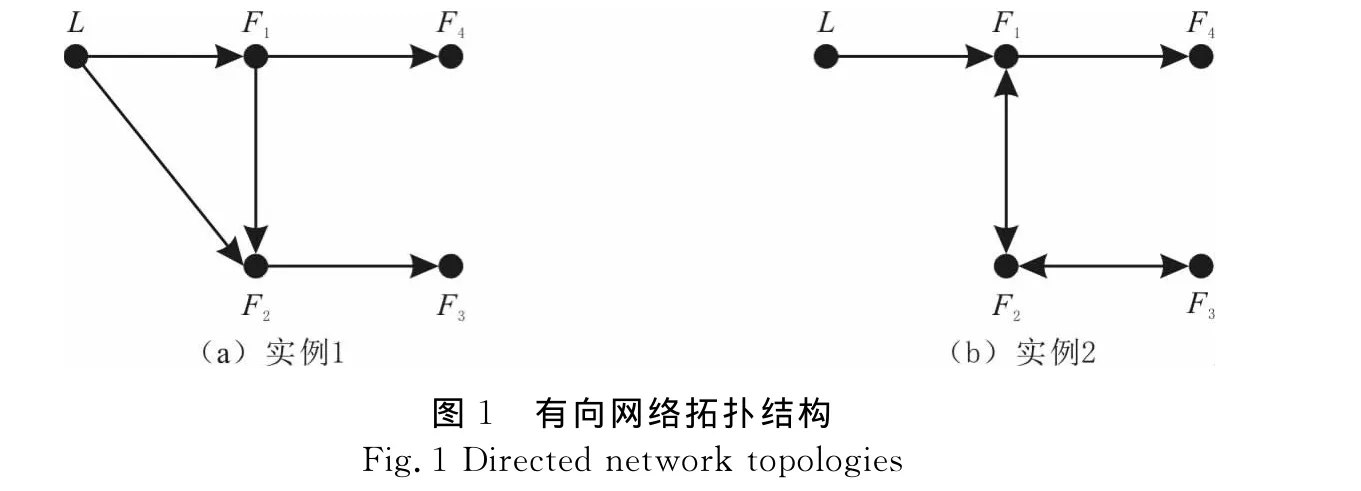
应用仿真实验验证文中算法的正确性，实验中实例1和实例2分别针对算法（3）和算法（6）进行网络一致性仿真研究，实例3应用算法（6）进行多车辆网络的编队控制.智能体之间的网络拓扑结构见图1，网络中共5个智能体，其中L代表多智能体网络中的虚拟领航者，Fi（i＝1，2，3，4）分别代表多智能体网络中的第i个跟随者.

4.1 实例1

实例1有向网络拓扑结构见图1（a）.由图1（a）可见，只有智能体1和2能够收到领航智能体的状态信息，并且该有向拓扑具有有向生成树，满足定理1条件.令虚拟领航者的状态为时变函数f（t，xr）＝cos t，针对多智能体网络（1）采用控制算法（3），得到各个智能体的状态变量轨迹（见图2）.由图2可见，所有智能体的状态渐近趋于一致，并且收敛于领航者的状态，实现一致性跟踪，与定理1结论符合.

4.2 实例2

实例2有向网络拓扑结构见图1（b）.由图1（b）可知，只有智能体1能够收到领航智能体的状态信息，并且该有向拓扑具有有向生成树，满足定理2条件.令虚拟领航者的状态为时变函数f（t，xr）＝cos t，并且令第i个智能体与领航状态位置的理想偏差为δei＝1-i，i＝1，2，3，4.针对多智能体网络（1）采用控制算法（6），得到各个智能体的状态变量轨迹（见图3）.由图3可见，所有智能体的状态与领航者状态通过快速调整之后渐近保持恒定偏差，实现相对状态保持期望偏差的渐近一致，与定理2结论符合.

4.3 实例3

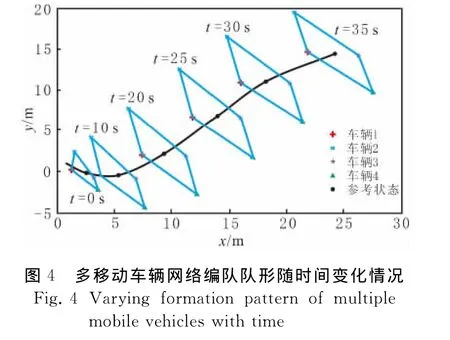
实例3验证算法（6）在多智能体网络编队控制中的有效性，考虑由4个移动车辆所构成网络的编队控制，有 向 网 络 拓 扑 见 图 1（b）.令 xr＝［30sin（πt／100），20sin（πt／50）］，为编队中心，4个移动车辆与编队中心的期望偏差为编队队形在t为0，10，20，25，30，35s时的队形见图4.由图4可见，在初始时刻，车辆之间队形不规则，在左右车辆网络渐近具有理想编队队形，并且在t为20s后一直保持稳定的理想队形.

5 结束语

针对一阶多智能体网络在有向固定通信拓扑情况下，只有部分个体已知时变领航参考状态的一致性问题，提出一致性控制协议，并通过图论、矩阵论及稳定性理论提出实现跟踪时变领航一致的充要条件及控制算法.将该控制算法拓展到智能体间具有固定相对状态偏差的情况，给出实现具有固定相对偏差一致的充要条件及控制算法，并将该控制算法应用到多移动车辆网络编队控制中.通过3个实例仿真实验验证基于文中算法的控制协议，实例1验证当且仅当网络拓扑具有有向生成树时，文中算法控制协议可以解决部分智能体在已知时变参考状态情况下的一致性追踪问题；实例2应用基于拓展算法的控制协议，验证所有智能体的状态与领航者状态能够渐近保持恒定偏差，实现相对状态保持期望偏差的渐近一致；实例3将相对状态偏差算法引入到多车辆的编队控制中，拓展多智能体编队的控制方法.

（References）：

［1］Zou Yunfei，Prabhakar R P.Distributed formation control of multiple aircraft using constraint forces［C］.Seattle：American Control Conf.，2008：644-649.

［2］Liu Huagang，Fang Hao，Mao Yutian.Distributed flocking control and obstacle avoidance for multiagent systems［C］.Xuzhou：Chinese Control Conf.，2010：4536-4541.

［3］Yan Jing，Guan Xinping，Luo Xiaoyuan.Multi-target pursuit formation of multi-agent systems［J］.Chinese Physics B，2011，20（1）：698-707.

［4］Jos'e Rodrigues，Dario Figueira.Leader-following graphbased distributed formation control［C］.Aveiro：Proceedings of Robotica，2008：71-77.

［5］Olfati-Saber R.Flocking for multi-agent dynamic systems：algorithmsand theory ［J］.IEEE Transactions on Automatic Control，2006，51（3）：401-420.

［6］Tanner H G，Jadbabaie A，Pappas G J.Stable flocking of mobile agents，partⅡ：dynamic topology［C］.Hawaii：Proceedings of the IEEE Conference on Decision and Control，2003：2016-2021.

［7］Alighanbari M，How J.Decentralized task assignment for unmanned air vehicles［C］.Seville：Proceedings of IEEE Conference on Decision and Control，2005：5668-5673.

［8］Olfati-Saber R，Shamma J S.Consensus filters for sensor networks and distributed sensor fusion［C］.Seville：Proceed-ings of IEEE Conference on Decision and Control，2005：6698-6703.

［9］Ren W，Beard R W，Atkins E M.Information consensus in multivehicle cooperative control［J］.IEEE Control Syst.Mag.，2007，27（2）：71-82.

［10］Olfati-Saber R，Fax J A，Murray R M.Consensus and cooperation in networked multi-agent systems［J］.IEEE Transactions on Automatic Control，2007，46（3）：215-233.

［11］Jadbabaie A，Lin J，Morse A S.Coordination of groups of mobile autonomous agents using nearest neighbor rules［J］.IEEE Transactions on Automatic Control，2003，48（6）：988-1001.

［12］Olfati-Saber R，Murray R M.Consensus problems in networks of agents with switch in topology and time-delays［J］.IEEE Transactions on Automatic Control，2004，49（9）：1520-1533.

［13］Ren W，Beard R W，McLain T W.Coordination variables and consensus building in multiple vehicle systems［M］.Lecture Notes in Control and Information Sciences，New York：Springer-Verlag，2004：171-188.

［14］Ren W，Beard R W.Consensus seeking in multi-agent systems under dynamically changing interaction topologies［J］.IEEE Transactions on Automatic Control，2005，50（5）：655-661.

［15］Moreau L.Stability of multi-agent systems with time-dependent communication links［J］.IEEE Transactions on Automatic Control，2005，50（2）：169-182.

［16］Lin Z，Broucke M，Francis B.Local control strategies for groups of mobile autonomous agents［J］.IEEE Transactions on Automatic Control，2004，49（4）：622-629.

［17］王垚，伍清河，王寅秋.切换拓扑一阶积分器网络量化趋同控制［J］.控制与决策，2013，28（3）：429-433.Wang Yao，Wu Qinghe，Wang Yinqiu.Quantized consensus of first-order Integrator networks with switehing topologies［J］.Control and Decision，2013，28（3）：429-433.

［18］纪良浩，廖晓峰.具有不同时延的多智能体系统一致性分析［J］.物理学报，2012，61（15）：150-202.Ji Lianghao，Liao Xiaofeng.Consensus analysis of multi-agant system with multiple time delays［J］.Acta Physica Sinica，2012，61（15）：150-202.