航行体出水空泡溃灭载荷特性研究

赵蛟龙，孙龙泉，张忠宇，姚熊亮

(哈尔滨工程大学船舶工程学院，150001哈尔滨)

航行体在水下运动过程中，其肩部会形成空泡，空泡在航行体运动过程中不断生长变化，最终会在航行体穿越水面过程中发生溃灭，溃灭载荷会对航行体的运动姿态产生影响，航行体结构可能受到破坏;因此对航行体出水空泡溃灭载荷进行研究具有相当的工程意义.文献［1］系统地总结了出水空泡流动的一些研究进展，就航行体穿越水面过程时的空泡溃灭现象进行了定性描述;文献［2］采用简化封闭模型，粗估了出水过程中空泡溃灭动压力的量级;文献［3-5］采用CFD方法及Singhal空化模型对航行体出水空泡溃灭问题进行了初步研究.

本文根据出水过程空泡溃灭的特点，将空泡溃灭过程分为空泡运动阶段和空泡溃灭冲击阶段，并基于该假设简化空泡溃灭的力学模型，进行力学分析，形成一套计算空泡溃灭载荷的方法.

1 航行体出水空泡溃灭模型的建立

根据航行体出水过程空泡的运动特征，将航行体出水空泡溃灭问题划为两个阶段分别进行研究，计算流程图如图1所示.

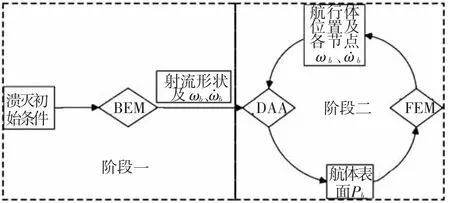
图1 航行体空泡溃灭载荷计算流程图

第一阶段基于势流方法根据不同发射条件得到初始空泡溃灭形态及运动过程，获得各个时刻空泡的运动速度及加速度，用于下一阶段溃灭冲击过程的计算.

在上一阶段得到空泡的运动过程后，第二阶段将空泡溃灭冲击航行体表面的过程近似为水射流冲击过程，采用NDAA方法计算射流冲击载荷，完成整个计算过程.

1.1 空泡运动阶段模型

航行体空泡溃灭初始时刻为航行体肩空泡与自由液面接触时刻，此时航行体肩空泡溃灭过程开始，即上文提出计算模型的第一阶段，通过势流方法获得肩空泡的初始条件及运动阶段的速度，为第二阶段的射流冲击过程提供初始条件.

由于空泡溃灭的时间较短，因此设流体是理想的、不可压缩的，整个物理模型如图2所示，则流体在流体域内满足.

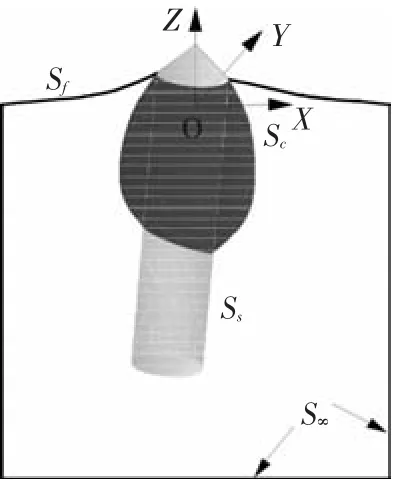
图2 空泡运动阶段物理模型

根据Green第三公式，则拉普拉斯方程变为ε(p)φ(p)=

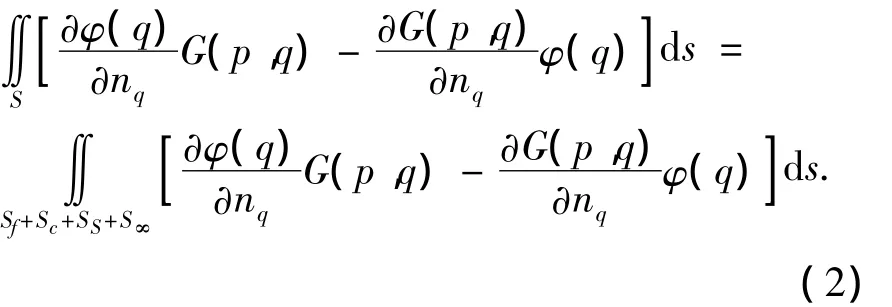
式中:p为流场中任意一点;q为边界上的积分点;nq为边界的法向量，以指向流域外为正;S为整个边界，包括自由液面表面Sf、航行体湿表面Ss、空泡表面Sc以及无穷远表面S∞;ε(p)是点p处立体角．

而三维空间的格林函数为

式中r为积分点q和流场中控制点p的距离．

此外，边界积分方程还应满足以下边界条件:

1)在航行体表面需满足法向速度不可穿透条件，即

式中v为航行体的运动速度．

2)无穷远处满足来流条件和扰动为零

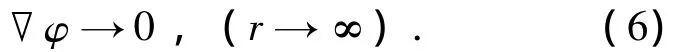
3)肩空泡表面动力学条件:

在肩空泡溃灭的过程中，空泡与航行体肩部接触部分的曲率较大，表面张力的存在将会使曲率减小，使该位置的空泡形状趋近于光滑.在空泡运动阶段，应考虑表面张力作用，如图3所示，则空泡表面受力平衡方程变为

式中:Pl为空泡外部的压力，Pg为空泡内部的压力，γ为表面张力，为曲面的主曲率．

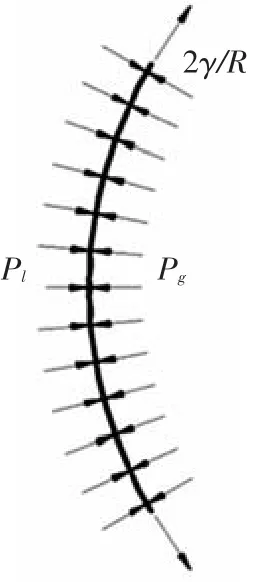
图3 空泡泡壁受力示意图

将上式带入伯努利方程，则其变为

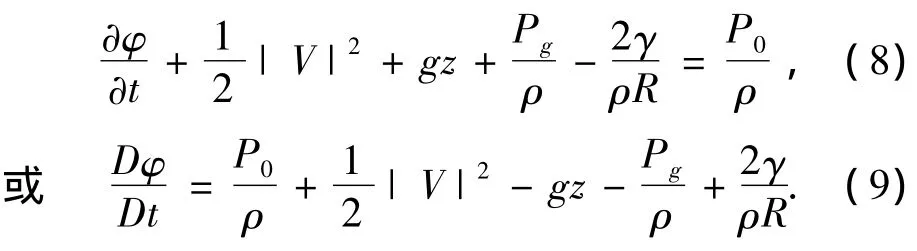
对于方程(2)的离散，采用七点高斯公式和等参变换［6-7］，将控制点离散到各个网格节点上，得到

式中:φj为j节点的速度势，ωj为j节点上的法向速度，Hij和Gij为对应的系数矩阵，m为模型节点个数．

为了书写方便，将上述方程写成矩阵形式，即

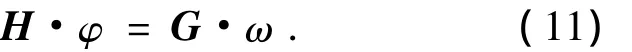
空泡表面上的速度势和自由液面上的速度势已知，法向速度未知;而航行体上法向速度已知，速度势未知，则可以对上述方程进行重新组合，以方便统一求解.将未知量移到方程的左端，已知量移到方程的右端，则方程变为

通过求解式(12)，可得肩空泡运动的法向速度ωb和加速度·ωb，ωsn为结构法向运动速度．

当求出空泡表面的速度以后，采用式(13)对自由液面进行位置更新，直至运动到航行体表面.

当求出空泡表面的运动速度以后，则可根据式(14)获得下一时刻的速度势

如此采用时域推进，直至空泡运动到航行体表面，并给出到达航行体表面空泡的法向速度ωb和加速度·ωb，用于空泡溃灭射流冲击计算．

1.2 溃灭冲击阶段模型

在空泡溃灭射流冲击阶段，水气混合，形成一股射流冲击到航行体表面.

假设流场为各向同性、无粘、无旋且可压缩的流体，流体域满足控制方程:

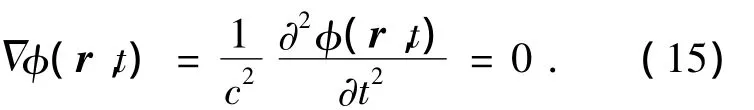
式中:c为水气混合物的压缩波速度，r为空间矢量坐标，t为时间坐标，φ为流体的速度势．

航行体运动的边界条件为

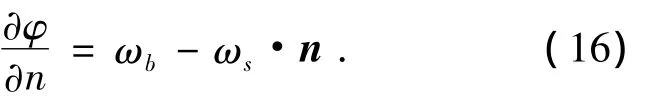
式中:ωs为结构弹性振动速度，n为法向坐标向量．

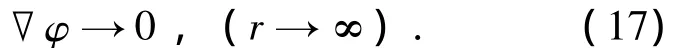
无穷远的边界条件为基于非线性双渐进方法的水柱冲击航行体表面的溃灭冲击力的计算公式［8-10］为

不考虑弹性振动时:

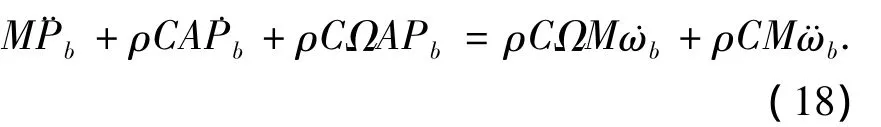
考虑弹性振动时:

计算出的载荷Pb作为局部载荷加载到航行体表面，获得航行体下一时刻的姿态及速度.

2 有效性验证

为验证本文方法的正确性，与某型号1∶1模型试验测得表面各点压力进行对比，图中对溃灭压力与时间均进行了无量纲处理:

式中:Pb为航行体表面压力，g为重力加速度，v为航行体垂向运动速度，L为航行体长度．

基于上文中所述方法对航行体出水过程进行分析，得到肩空泡的运动形式，如图4所示.

如图4(a)所示，当肩空泡与自由液面相接触的时候，由于表面张力的作用，肩空泡的内外压差发生突变，空泡内部平衡被打破，使空泡泡体向航行体运动.空泡开始发生溃灭，水汽混合形成“射流”，冲击到航行体表面.当空泡运动至航行体表面时，即开始进入溃灭冲击阶段，如图4(b)所示.记录该时刻的溃灭冲击速度和加速度，用于下一阶段溃灭载荷的计算.在表面张力以及内外压差持续作用之下，肩空泡不断被压缩，空泡体积不断变小，空泡扰动势不断增加，表现为空泡溃灭冲击速度不断增大.随着空泡被逐步压缩，其将沿着航行体长度方向的持续不断地溃灭，航行体将会受到溃灭载荷持续不断冲击作用，如图4(c)～(g)所示.最终整个泡体运动至航行体表面，肩空泡完成溃灭.

为了验证计算方法的合理性，本节选取迎流面处距航行体顶端为 0.30 L、0.4 L、0.45 L、0.50 L 4个位置测点，将溃灭冲击载荷的数值解与试验值进行对比分析，具体如图5所示.

由图5和表1可知，由于空化现象的影响，在未发生溃灭时，本文的空泡模型并未考虑空泡的前期脉动，空泡区内的压力为空化压力的恒定值.但实际情况下空泡内部处于一个脉动的准平衡状态，因此试验值的空泡区的压力存在振荡的现象.随后空泡溃灭产生一个较大的溃灭冲击峰值，并迅速下降.从不同位置的溃灭载荷峰值的时刻，可以看到空泡将沿着航行体的长度方向自上而下逐步发生溃灭，这与图4中肩空泡的运动过程吻合，间接证明本文计算方法的正确性.

图4 空泡运动过程

对于空泡溃灭冲击载荷的峰值，数值解和试验值吻合良好，数值解相对较小.其中，最大误差为6.06%，平均误差为2.43%.但对于脉宽的误差相对较大.这是由于溃灭冲击载荷引起了结构的应力波效应，应力波在航行体内部透射、反射，使实测到航行体测点的载荷的脉宽减小.且当应力波在航行体中传播时，由于航行体结构的卸载效应，使溃灭载荷在航行体出水后仍在一定范围内振荡.

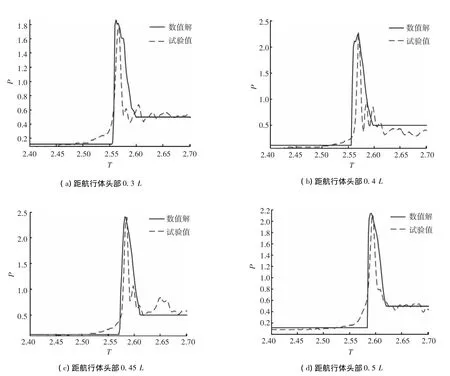
图5 不同位置处溃灭冲击载荷数值解和试验值对比

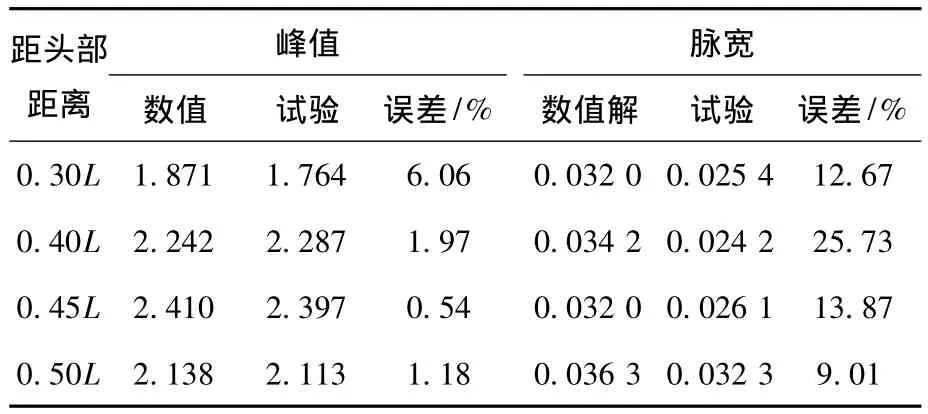
表1 数值解和试验值溃灭冲击载荷峰值、脉宽对比

3 弹性振动对溃灭射流冲击载荷特性影响

为明确弹性振动对航行体出水过程空泡溃灭载荷的影响，建立航行体刚体有限元模型，采用与弹性体模型相同的初始条件和参数，分别选取距航行体头部0.30 L、0.40 L、0.45 L及0.50 L处的溃灭冲击载荷进行对比分析，总结弹性振动对于溃灭冲击载荷特性的影响.

由图6和表2可知，由于弹性振动的存在，空泡溃灭冲击载荷的峰值有一定的下降.以刚体溃灭冲击载荷为基准，不同位置弹性体溃灭冲击载荷峰值分别下降0.5%、7.0%、5.2%以及3.4%.但溃灭冲击压力脉宽有一定的增加，不同位置弹性体的溃灭冲击载荷脉宽分别增加3.2%、9.6%、3.2%以及0.8%.可见航行体的弹性振动对航行体出水溃灭冲击压力影响相对较小.这是由于溃灭冲击载荷的频率与航行体结构局部弹性振动频率及航行体自身固有频率有明显区别，在航行体穿越水面过程中，空泡溃灭冲击过程未激起结构本身的弹性振动.

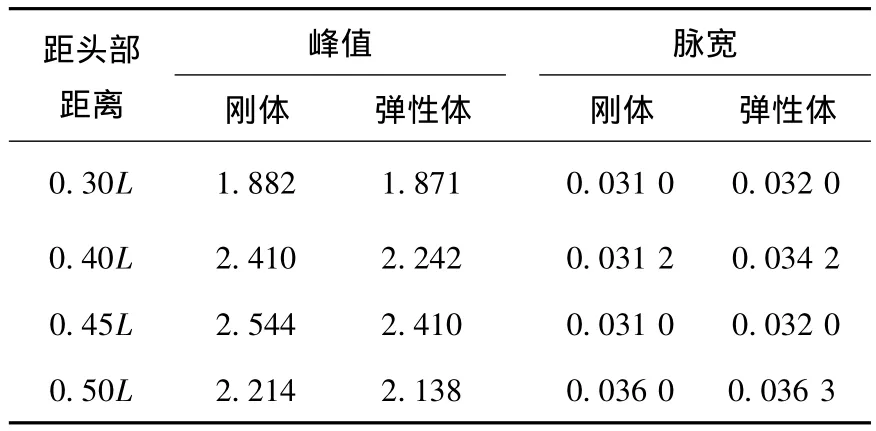
表2 刚体与弹性体溃灭冲击载荷峰值、脉宽对比

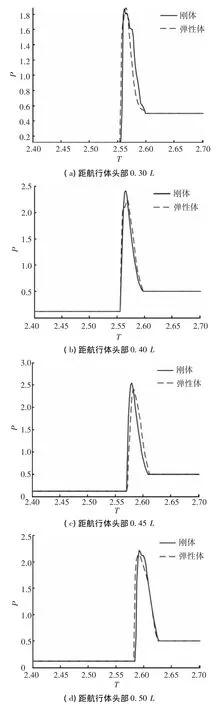
图6 刚体和弹性体不同位置处溃灭冲击载荷对比

4 结论

本文主要从空泡溃灭的物理现象入手，将空泡溃灭过程分为空泡运动阶段和空泡溃灭冲击阶段，并基于该假设进行力学分析，简化空泡溃灭的力学模型，形成一套计算空泡溃灭载荷的方法，得到以下结论:

1)采用本文方法得到的数值计算结果与试验值结果相比，冲击压力峰值平均误差为2.43%，脉宽平均误差15.3%，两者吻合较好，验证了方法的合理性.

2)肩空泡溃灭过程中，空泡体积不断变小，肩空泡溃灭区域从两侧向中间移动，整个溃灭历程无量纲时间在0.15左右.

3)考虑结构弹性振动的空泡溃灭冲击载荷的峰值有所下降，脉宽有所增加;峰值下降4%左右，脉宽增大4.2%左右，弹性振动对航行体空泡溃灭冲击载荷影响不大.

［1］颜开，王宝寿.出水空泡流动的一些研究进展［C］//第二十一届全国水动力学研讨会暨第八届全国水动力学学术会议暨两岸船舶与海洋工程水动力学研讨会文集.济南:中国力学学会，2008:822-827.

［2］罗金玲，毛鸿羽.导弹出水过程中气/水动力学的研究［J］.战术导弹技术，2004，7(4):23-25.

［3］王一伟，黄晨光，杜特专.航行体垂直出水载荷与空泡溃灭机理分析［J］.力学学报，2012，44(1):39-48.

［4］SINGHAL A K，ATHAVALE M M，LI HY.Mathematical basis and validation of the full cavitation model［J］.Journal of Fluids Engineering，2002，124(3):617-624.

［5］权晓波，李岩.航行体出水过程空泡溃灭特性研究［J］. 船舶力学，2008，12(4):545-549.

［6］YAO X L，ZHANG A M.A numerical investigation of bubble dynamics based on the potential-flow theory［J］.Journal of Marine Science and Application，2006，5(4):10-21.

［7］张阿漫，姚熊亮.近自由面水下爆炸气泡的运动规律研究［J］.物理学报，2008，57(1):339-353.

［8］姚熊亮，孙士丽，陈玉.非线性双渐进法应用于水中结构瞬态运动的研究［J］.振动与冲击，2010，29(10):9-15.

［9］GEERS T L，FELIPPA C A.Doubly asymptotic approximations for vibration analysis of submerged structures［J］.J Acoust Soc Amer，1980，73:1152-1159.

［10］KWON Y W，FOX P K.Underwater shock response of a cylindersubjected to a side-on explosion［J］.Computers＆ Swucrures，1993，48(4):637-646.