无人水面艇目标图像自适应分割算法

马忠丽，梁秀梅，文 杰

(哈尔滨工程大学自动化学院，150001哈尔滨)

水面目标图像分割技术是水面舰船、舰艇等视觉侦查系统目标图像处理的一项关键技术，是舰船等捕获、精确跟踪与识别目标的重要前提和基础.水面视觉传感器采集的目标图像中，一般以海水、天空为背景，而图像由于受水面环境与天气的影响，会附加很多噪声使图像目标细节模糊不清.刘小霞等［1］对红外水面舰船目标图像进行归一化投影后，采用改进的OTSU阈值算法分割，算法简单但运行不稳定.汪成亮等［2］提出应用二维小波变换对江面船舶图像提取边缘轮廓，算法抗噪能力强，提取效果好，但算法理论结构较为复杂.李棉［3］对陆地上含有不同目标的图像用迭代OTSU阈值分割算法与基于Mean-Shift(均值漂移)的分割算法进行分割，实验结果表明基于Mean-Shift的图像分割算法运行速度快且结果稳定.

Mean-Shift是一种无参数核密度估计的迭代算法，Brooks等［4］将该算法应用到图像分割、视觉跟踪等领域，并证明了算法的有效性.Mean-Shift算法通过非参数密度估计进行区域像素点聚类从而实现图像分割，由图像特征空间中的空间域带宽与灰度域带宽参数决定图像分割效果［5-6］.Zheng等［7］通过设定初始带宽，然后按照带宽逐步增加的方式来寻找图像的理想带宽，从而实现图像的分割.Comaniciu等［8-9］图像分割研究中，运用动态和自适应选取带宽的方法降低了算法的迭代次数.Mayer等［10］通求求取参考点K-最近邻距离得到带宽参数，但是当图像分辨率较高时，计算量较大.Mahmood等［11］根据改进的贝叶斯理论，自适应确定Mean-Shift算法中的灰度域带宽，然而空域带宽的设置直接影响图像的最终分割结果.

考虑水面目标图像特点，这里给出一种改进的自适应Mean-Shift算法，将其用于水面艇视觉系统的水面目标分割，仿真结果证明了该算法的可靠性.

1 Mean-Shift图像分割算法

1.1 Mean-Shift算法基本原理

文献［12］对Mean-Shift图像分割算法原理做了详细推导，其原理为

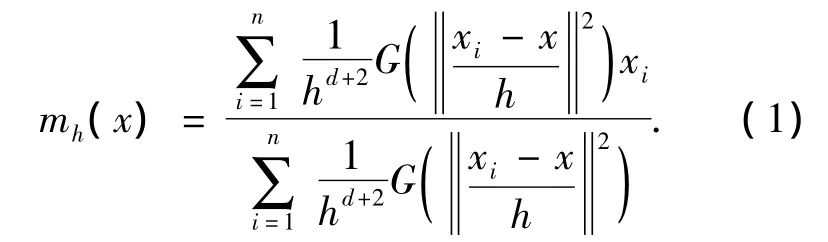
其中:mh(x)称为Mean-Shift迭代公式;在d维特征空间中，G(x)为核函数，决定了采样点xi与中心点x之间的相似性;h为带宽参数，带宽参数不但决定了参与迭代的采样点数量，而且还会影响算法的收敛速度和准确性．

令Mh(x)=mh(x)-x为Mean-Shift向量，模态点的搜索即是通过mh(x)的迭代计算寻求使mh(x)→x的点，搜索过程也可以描述为，每次迭代计算都是从当前采样点指向密度较高的区域中的采样点，即

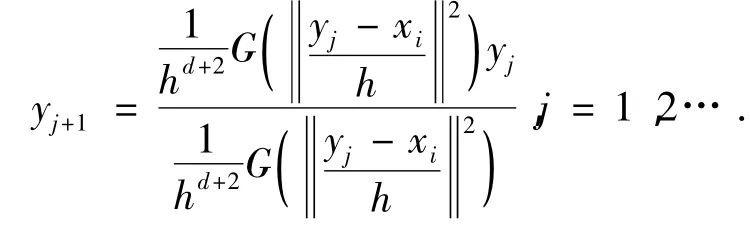
算法在该点的收敛性已得到验证［13］.

Mean-Shift算法的聚类运算是在一个联合空间范围域中进行，这种方式有利于对水面艇视觉系统获得的近距离与远距离目标图像进行处理.联合域内核是一种基于空间域与值域的对称核，表示为

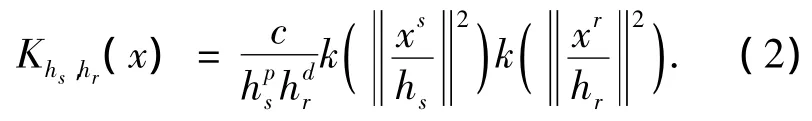
其中:c为对应的标准化常量;hs是p维空间域，hr是d维灰度域核带宽，实际应用中，这两个参数的设定决定着最终目标分割效果;xs表示空间域;xr是特征向量的值域;k(x)表示空间域和值域共同的轮廓．

1.2 Mean-Shift算法图像分割

Mean-Shift算法图像分割基本思想是先利用式(1)进行模态搜索，得到模态点，从而对目标图像进行平滑滤波，然后对模态点包含的像素进行统计，将像素数量少的那些模态点聚合到邻近的模态中，从而实现目标图像分割.

给定Mean-Shift迭代式(1)的初始条件，包括模态搜索的起始位置，核函数G(x)，带宽(hs，hr)，以及误差ε=0.01和区域聚合的最小限参数M．给定初始条件后Mean-Shift算法主要分平滑滤波和区域聚合两步进行.其中平滑滤波步骤如下:

1)令 j=1，yi，1=xi，对该像素点 xi，计算mh(xi);

2)如果|mh(xi)-xi|＞ε，移动窗口中心到下一点，并且标记 yi，j+1，利用式(1)求得该点的mh(xi)，直到 Mean-Shift向量满足 |mh(xi)-xi|＜ε，表明初始点的模态点已找到，记录该模态点，将该模态点的像素坐标赋给xi，且将其像素值保存为 yi，c;

3)将第2)步每次迭代运算得到的像素点xi和收敛值yi，c保存在zk中，即zk={xs别表示像素点空间上的位置信息和灰度特征的值域信息．

将经过平滑滤波后的图像进行区域聚合处理，具体步骤如下:

1)根据上一步平滑滤波图像中每个像素点的空域和值域信息，将模态点zk中同时满足值域距离小于hr和空域中距离小于hs的点聚合在一起，即{zk∈ Cp}p=1，2，…，m;

2)将模态点聚合后的区域中像素总数小于M的区域剔除．

2 改进自适应Mean-Shift分割算法

为解决传统Mean-Shift算法的全局固定带宽适用性不强的问题，本文结合Mahmood确定灰度域带宽的方法，通过估计中心点邻域的灰度分布，自适应确定空间域带宽从而实现Mean-Shift迭代算法中带宽参数的自动获取，达到自适应分割的目的.

2.1 空间域带宽自适应计算

在图像平滑滤波操作中，核函数的作用范围由空间域带宽决定，对图像平滑效果有着一定的影响.在利用固定带宽参数分别对水面艇视觉系统采集到的远、近距离目标视频帧进行处理时，通常会出现一方过平滑或欠平滑的现象，带宽参数手动调节无法实现自适应目标分割效果，为解决这一问题，提出了一种自适应空间域带宽计算方法.

自适应空间域带宽计算方法如下:首先设定1个空域带宽初值hs0，参考像素点xi，假设该点灰度值为Ti．在以xi为中心，边长为(2×hs0+1)的正方形窗内，统计窗口中与参考中心点xi灰度值相近的像素点数目mi，本文中将满足|Tj-Ti|≤5的像素点认为是灰度值相近的像素点，其中Tj为窗口内中心点以外的像素点的灰度值．当mi/(2×hs0+1)2＜0.8时认为hs0为该像素点的自适应带宽，记为hi，且将该带宽值存入矩阵H中．若不满足mi/(2×hs0+1)2＜0.8则令hs0=hs0+1，然后继续统计窗口大小更新以后的灰度值相近的比例，直到满足总像素数小于80%的条件为止．其算法流程如图1所示．

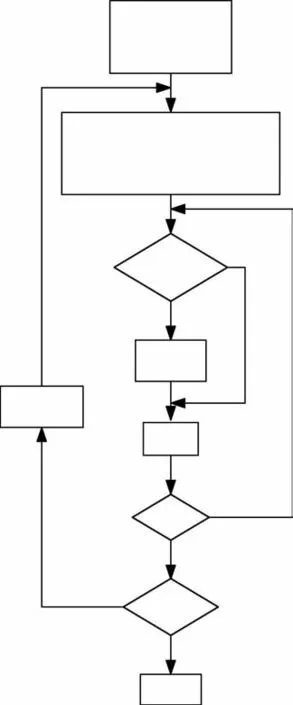
图1 空域带宽自适应计算流程

2.2 灰度域带宽自适应计算

本文灰度域带宽的自适应计算思想如下:设局部数据类s，x为该类中的样本点，通过求解数据类s的后验概率密度函数P(s|x)，从而得到灰度域带宽．假设在类s中点xi的最近邻域内的数目为K，K＜n，这里的最近邻域为前面所求的该参考点空间域带宽，计算空间窗口内所有除参考样本点xi以外的点与xi的欧几里得距离，并且将距离按照升序的方式排列，即

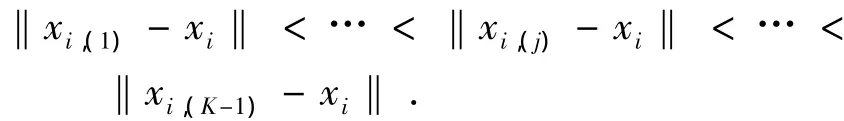
其中xi，(j)≠xi且j=1，2，…，K-1．

由此带宽的概率密度函数定义为

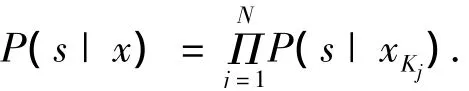
其中P(s|xKj)是局部数据类s对xKj的Kj最近邻域内样本点的条件概率，{Kj，j=1，2，…，N}是一组具有不同大小的N个邻域．

s在Kj整个范围中的概率估计描述为

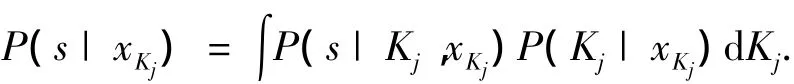
由贝叶斯准则可知

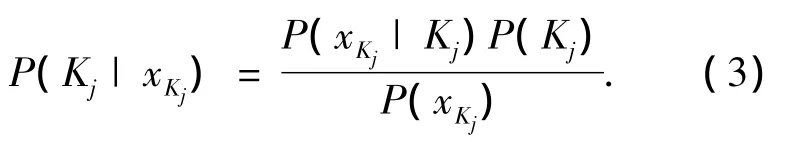
其中:P(xKj|Kj)表示数据样本基于Kj最近邻域的概率，Kj服从均匀分布，定义其范围为［h0，hs(xi)］，hs(xi)对应于每次Mean-Shift迭代参考点xi的空间窗带宽，令Kj=hj满足

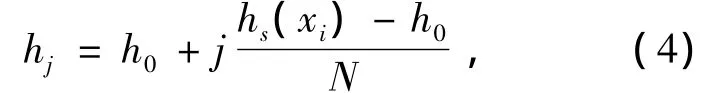
则所包含的采样点数目为Zj=(2×hj+1)2-1．而局部变量s可通过下面的表达式获得:

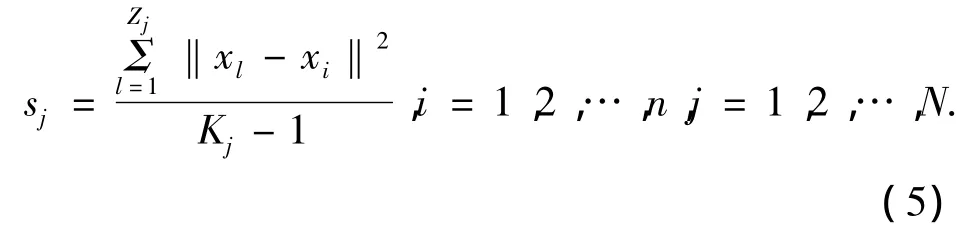
其中xl为特征点xi最近邻窗口中的像素点的灰度值．

采用伽马分布对局部数据类s建模，伽马分布表示如下:

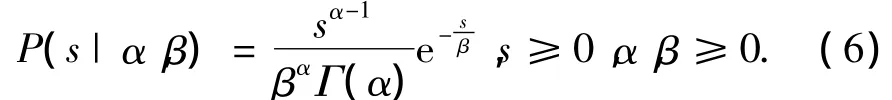
其中:α为形状参数，β为尺度参数，利用极大似然估计的方法对其进行估计，通过求取局部数据类s伽马分布的期望从而得到灰度域带宽，即hr(xi)=，i=1，2，…，n．由此得到联合域的内核立体图如图2所示．

自适应Mean-Shift算法的伪代码如下所示.

输入:目标的灰度图像A;

输出:平滑滤波图像和分割后图像.

begin

hs=hs-adaptive(A);%根据图1的流程图确定每个像素点的空域带宽，

%hr=hr-adaptive(A，hs);

for按图像行列逐点搜寻

判定每个参考像素点对应hs是否为1:

if(不为1)

则根据式(3)～(4)计算对应的Zj表现概率，选取最优概率的Kj值，由式(5)确定sj;

以sj为一组样本数据类，根据式(6)，由极大似然估计法求得参数α和β;从而求得对应参考像素点的灰度域带宽hr(xi)=.

if(为1)直接由式(5)求得sj，代入式(6)，运用极大似然估计法求取参数α和β;

end

for图像的每一个参考像素点

B=meanshiftsmooth(A(，)，hs(:，:)，hr(:，:)，gauss);%根据自适应得到的带宽，利用核函数kernelmatrix以及式(3)得到平滑滤波图像

B-Seg=meanshiftseg(B)%根据前面1.2节所述的方法，得到最后的目标分割结果．

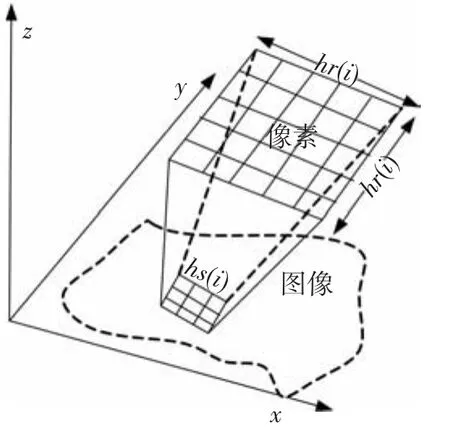
图2 联合域核立体图

3 水面艇目标图像分割实验与分析

本文水面艇图像采集系统摄像器件为CMOS摄像头，动态分辨率1 280×960，最大帧频60 FPS，像素500万;算法的仿真实验在Intel Core i5-3210M双核CPU、4 GB内存，matlab7.6软件环境下实现.

得到的水面图像分为近、远距离目标图像，仿真内容包括:1)空间域与灰度域带宽自适应计算分析;2)从视觉角度与分割误差两方面验证算法有效性和准确度;3)算法对水面目标处理的适用性验证.

将图像转换为352×288的灰度图像.图3(a)、(b)是近距离水面目标，景深距离均为20.52 m(艇上激光测距得到)，图3(a)图像的背景比较简单，船只的对比度相对较高，而图3(b)中水面的波纹较为突出，图像中目标和背景的灰度相似，对比度不明显.图3(c)、(d)是由水面艇实际远距离拍摄的水面目标，图3(c)为远景图像，其背景较清晰，图3(d)背景较暗，对比度低，景深距离分别为151.45、190.32 m.

图3 水面目标灰度图

图像的全局对比度公式为

式中r(i，j)为相邻像素点灰度值的差值，p(i，j)为灰度值差为r的分布概率．图3中各图像的对比度如表1所示．

表1 图3中各图像对比度

3.1 空间域与灰度域带宽自适应计算分析

截取图3(b)中目标与背景的1个小区域图像如图4(a)，区域尺寸为39×16，图4(b)为该子区域灰度分布图，对该区域进行平滑操作后的灰度分布如图4(c)所示，图4(d)为分割后的灰度分布图.

在图3(b)中目标、背景区域各选取1个像素点作为参考点，这里的参考像素点坐标选取为(89，38)、(9，22)，带宽的自适应计算流程如下:

坐标为(9，22)的像素点灰度值为56，该点附近的灰度分布值如图5(a)所示，图5(a)中值1为满足|Tj-Ti|≤5条件的像素点，值0表示不满足该条件的像素点，由此得到此像素点处空间域带宽的值为3．则在［1，3］的范围内，利用贝叶斯准则得到该邻域内的K值分布结果如图5(c)，因此取K=2，此时对应的该像素点灰度域带宽值为53．

在坐标为(89，38)的像素点，其对应灰度值为140，对其邻域的灰度分布估计值如图5(b)，从而得到空间域带宽值为6．在［1，6］范围内，利用贝叶斯准则得到该像素点邻域内K的分布结果如图5(d)所示，从而得到K=4，此时其灰度域带宽为109．

由以上的自适应带宽计算结果可以看出，本文自适应带宽计算方法保证了在密度较小的区域自动选取较小的空域带宽值，在密度较大的区域中则使用相对较大的空域带宽值，而灰度域带宽的计算则与其对应的空间窗大小紧密相关，在目标和背景中能自适应的选取不同的带宽.

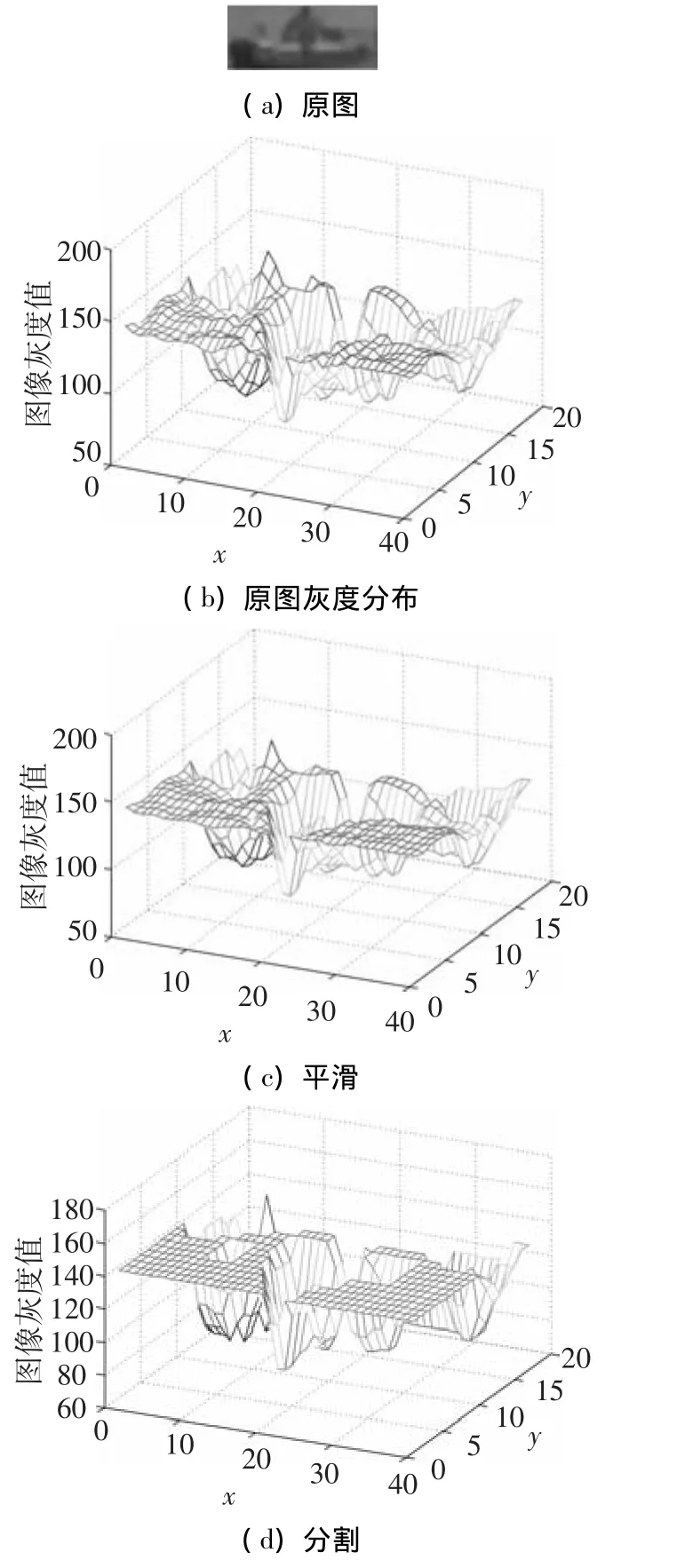
图4 子区域平滑分割前后灰度分布对比

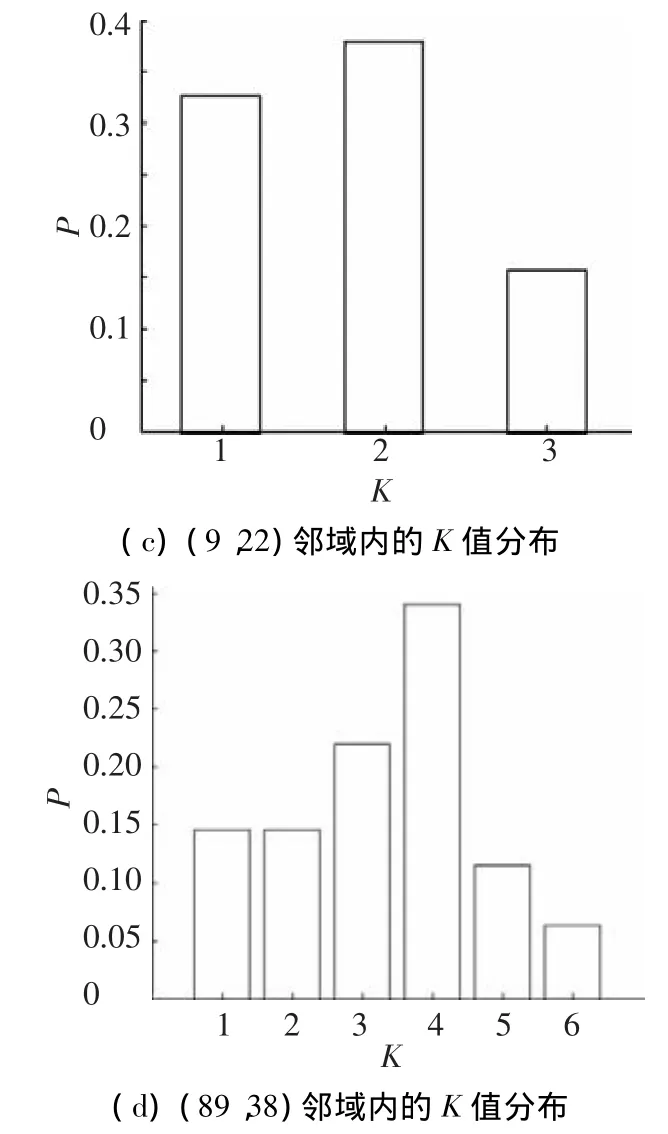
图5 参考点对应带宽自适应计算过程

3.2 本文算法的有效性与准确度验证实验

Mean-Shift算法中，带宽参数主要影响图像的平滑滤波过程，为后续分割过程做铺垫;另外一个影响分割结果的因素是区域聚合最小限参数M．实验中，算法中的区域聚合最小限参数M设置相同的值.

为了说明本文算法的有效性，将文献［7］提出的带宽获取方法与本文自适应获取带宽的方法进行分割效果对比.图6和图7是文献［7］Mean-Shift算法的平滑和分割结果，图8和图9是本文自适应Mean-Shift算法的处理结果.

图6 文献［7］算法的图像平滑效果

图7 文献［7］算法的图像分割效果

如图6所示，文献［7］通过逐步增加带宽值直到得到最终理想带宽的方法，由于得到的带宽仍然是全局带宽，所以该方法的平滑结果会出现如图6(a)中箭头所示的局部平滑不均匀现象，对于近距离目标图像会出现局部细节欠平滑现象，远距离目标则容易出现过平滑的现象，会影响最终分割结果的精度.而本文自适应分割算法在对图像的平滑操作过程中同时考虑了参考点的空间窗大小和其邻域中像素点的灰度值信息，在视觉上取得了更好的平滑效果.

图8 本文自适应Mean-Shift算法的图像平滑效果

图9 本文自适应Mean-Shift算法的图像分割效果

为说明本文算法的有效性，本文从客观实验的角度来进行验证.对图3中的4幅图分别进行手工分割，并作为该目标的标准分割图，将手工分割结果与本文算法分割结果二值化，计算本文自适应分割算法的分割结果与标准分割结果之间的误差.其中手工分割结果二值化图像如图10～13中图(a)所示，本文算法分割结果的二值化图像如图10～13中图(b)所示，分割误差的二值化图像如图10～13中图(c)所示，计算分割误差的公式为

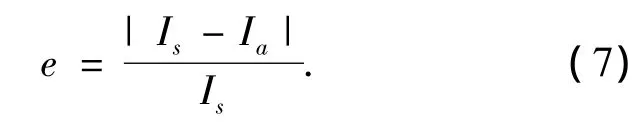
式中Ⅰs表示标准分割的二值化图像中目标区域(白色区域)所含的总像素数，Ⅰa表示本文算法分割后二值化图像中目标区域的总像素数．

根据式(7)，本文算法对图3的分割误差如表2所示，对于近距离的水面目标图像，其分割误差小于7%，对于远距离的水面目标图像的分割误差小于10%，由表中数据以及结合图6～9的主观评价结果说明本文算法分割后没有造成严重的目标失真现象，达到了目标分割的目的，并且分割效果较好.

表2 本文算法目标分割误差

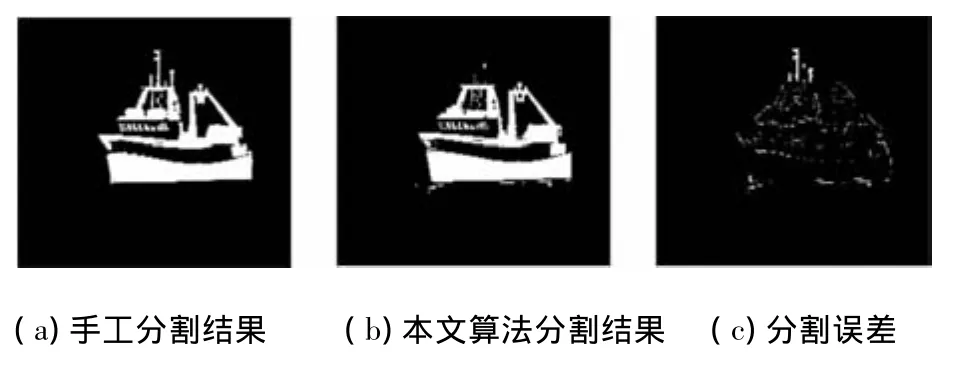
图10 图3(a)分割对比

图11 图3(b)分割对比

图12 图3(c)分割对比

图13 图3(d)分割对比

3.3 本文算法的适用性验证实验

对于水面目标图像，特别是远距离水面目标图像，通常目标和背景的对比度不明显，目前常用基于OTSU的自适应阈值分割算法来实现水面目标图像的分割，为了进一步说明本文算法适用于水面目标图像分割，将本文自适应Mean-Shift分割算法与OTSU分割方法进行对比分析，分割结果对比如图14～15所示.

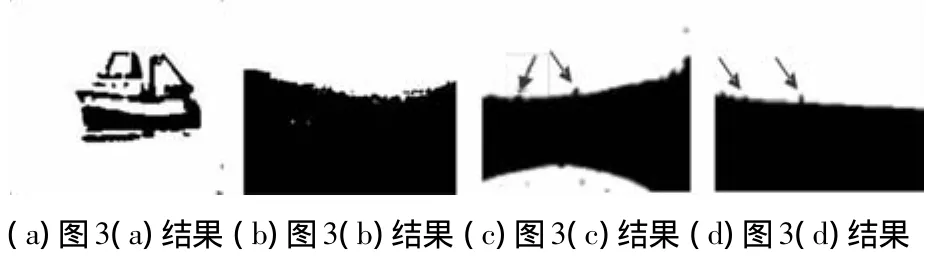
图14 基于OTSU的自适应阈值分割结果

图15 本文算法分割结果

基于OTSU阈值分割算法的分割结果如图14所示，本文算法的分割结果如图15所示.从图14(c)、(d)可以看出基于OTSU的自适应阈值分割算法能检测出海天线处的目标，但是分割后得到完整的目标较为困难，分割后含有许多海面背景部分.从图14(b)可以看出，当目标位于海面处而且当目标灰度与海面近似时，OTSU分割方法分割后无法得到目标.而从图15(b)中可以看出，本文算法能自动分割出目标，而且分割目标较为完整.从图14～15的整体对比也能明显看出本文算法优于OTSU算法，说明本文算法适合于水面目标图像的分割.

4 结论

1)改进自适应Mean-Shift算法的水面图像分割技术，能很好实现空间域带宽与灰度域带宽参数的自适应计算.测试能够体现出在图像灰度密度较高的区域实现了较小空域带宽的选择，在图像灰度相对较小的区域实现了较大空间域带宽的选择.而灰度域带宽和空域带宽紧密联系，结合贝叶斯准则选择对应空间窗的灰度点.

2)大量实验结果表明改进自适应Mean-Shift算法能够完成对水面目标图像实现较好的、整体度较高的分割.

3)但研究也显示算法还存在分割准确度的不确定性、不可靠性，当图像信息量大时运行速度会下降、分割效果不理想等缺点和问题.因此，对算法中的选取采样点的策略以及分割区域合并过程中的参数选取方法是下一步研究重点.

［1］刘小霞，徐贵力.嵇盛育.一种改进的舰船红外图像分割算法［J］.传感器与微系统，2008，27(6):37-39.

［2］汪成亮，汪连伟.基于特征的江面轮船识别算法［J］.计算机应用研究，2011，28(6):2352-2354.

［3］李棉.红外图像目标分割方法研究［D］.西安:西安电子科技大学，2011.

［4］SHEN C H，BROOKS M J.Fast global kernel density mode seeking:applications to localization and tracking［J］.IEEE Transactions on Image Processing，2007，16(5):1457-1469.

［5］PARK A ，KIM J，MIN S，et al.Graph cuts-based automatic color image segmentation using mean shift analysis［C］//In:Proceedings of the Conference on Digital Image Computing:Techniques and Applications.Piscataway:IEEE，2008:564-571.

［6］LI P F，WANG S R，JING J F.The segmentation in textile printing image based on mean shift［C］//In:Proceedings of the 10th Conference on Computer-Aided Industrial Design and Conceptual Design.Piscataway:IEEE，2009:1528-1532.

［7］ZHENG L Y，ZHANG J T，WANG Q Y.Mean-Shiftbased color segmentation of images containing green vegetation ［J］. Computers and Electronics in Agriculture，2009，65(1):93-98.

［8］COMANICIU D.An algorithm for data-driven bandwidth selection［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2003，25(2):281-288.

［9］COMANICIU D，RAMESH V，MEER P.The variable bandwidth Mean-Shift and data-driven scale selection［C］//Proceedings of Eighth IEEE International Conference on Computer Vision，2001.Piscataway:IEEE，2001:438-445.

［10］MAYER A，GREENSPAN H.An adaptive Mean-Shift framework for MRI brain segmentation［J］.IEEE Transactions on Medical Imaging，2009，28(8):1238-1250.

［11］MAHMOOD Q，CHODOROWSKI A，MEHNERT A.A novel Bayesian approach to adaptive mean shift segmentation of brain images［C］//2012 25th International Symposium on Computer-Based Medical Systems(CBMS).Piscataway:IEEE，2012:1-6.

［12］CHENG Y Z.Mean shift，mode seeking，and clustering［J］. IEEE Transactionson Pattern Analysisand Machine Intelligence，1955，17(8):790-799.

［13］李乡儒，吴福朝，胡占义.均值漂移算法的收敛性［J］.软件学报，2005，16(3):365-374.