基于改进人工鱼群算法的连续潮流电压稳定性研究

吴昊，董文辉

（江西省电力公司检修分公司，江西 南昌 330096）

0 引言

由于静态电压稳定分析因其简单易行且能为调度运行人员提供判断电压稳定性的有效指标，受到极大的重视和发展。利用连续潮流可以有效地得到完整的λ－V曲线［1－3］，获得负荷临界状态的潮流界，并用U－Q模态分析求得的灵敏度信息进一步确定薄弱域［4］，为运行人员提供有效的预防手段。

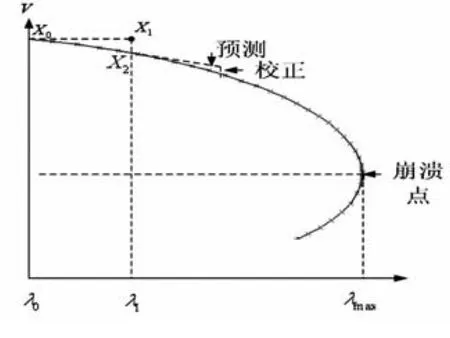
图1 连续潮流法

目前普遍认为变压器的调节、PV节点电压以及无功补偿容量等控制变量对电压稳定性有较大的影响［5－8］。本文考虑负荷特性影响，采用多目标函数非统一模型解法——乘除法，基于改进人工鱼群算法的连续潮流对变压器分接头、PV节点电压及无功补偿容量进行多目标优化，求取最大电压稳定裕度及电压偏移质量最小值，从而提高电压稳定性。

1 静态电压稳定的理论基础

1.1 系统连续潮流模型

利用连续潮流方法可以克服常规潮流在临界点附近不能收敛的问题，有效地绘制完整的λ－V曲线［6－8］，如图1所示。

设系统有N个节点，包括Npq个PQ节点，其中无功功率越限的PV节点用惩罚函数处理，Npv个PV节点和一个平衡节点，负荷模型为ZIP模型，则节点i的注入功率方程为:

式中PGi、QGi、QCi分别为有功、无功出力及无功补偿量;PLi、QLi分别代表有功、无功负荷;λ 为负荷增长水平，a、b、c及a1、b1、c1 分别为有功与无功负荷阻抗分量、电流分量、功率分量;Ui、Uj、θij分别为节点i和j的电压幅值和节点i与j之间的电压相角差;Gij、Bij分别为节点导纳阵第（i，j）个元素的实部和虚部，L为步长，K1、K2、K3为常数，考虑控制变量κ，将式（1）简化后写成矩阵和向量形式为:

式中X为状态变量，即电压幅值和相角。

1.2 优化数学模型

（1）Δλ作为静态稳定裕度，在负荷增长中，稳定裕度与系统中的一些控制变量有关，通过对控制变量优化，可有效提高Δλ，完善λ－V曲线。在此，目标函数为最大的Δλ，即电压崩溃时的负荷水平与当初的负荷水平之差，则采用目标函数为:

控制变量包括无功出力、无功补偿量、变压器档位等。同时以负荷节点电压质量和无功出力为惩罚项，则根据（3）采用扩展的目标函数为:

等式约束条件为（2），不等式约束为:

控制变量的不等式约束条件为:

式（5）、（6）中U、Umin、Umax分别为PQ节点初始电压及其下限与上限值，QG、QGmin、QGmax为PV节点初始值及其下限与上限值;式（5）中UG、UGmin、UGmax分别为PV节点初始电压及其下限与上限值，Tn、Tnmin、Tnmax为变压器分接头初始值及其下限与上限值，C、Cmin、Cmax为无功补偿量初始值及下限与上限值，α、β为惩罚因子。

（2）电压偏移量最小:

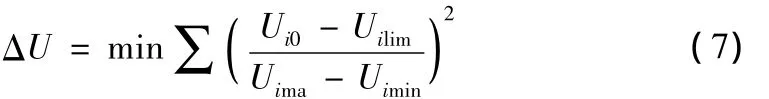
式中Ui0、Uimin、Uimax、Uilim分别为PQ节点初始电压、下限与上限值以及极限值。

1.3 多目标函数处理

在多目标优化中，由于对多个子目标同时优化，而这些被同时优化的子目标之间往往又相互冲突，照顾了一个子目标的“利益”，同时必然导致其它至少一个子目标“利益”受到损失［9－10］，因而难以比较。现在我们对多目标问题（VP）*改进，并假设对一切x∈R均有:

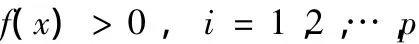
乘除法基本思想很简单，要求分子越大、分母越小整个目标函数就越好，于是可将（VP）*转化成统一的极大化问题:

所以根据式（4）、（7）得出的多目标函数为:

它们的最优解都是这就是乘除法的几何依据，因为评价函数maxF（X）=显然是F（X）的严格单增函数，故其任一最优解都是有效解。

2 改进人工鱼群算法在电压稳定中的应用

在传统鱼群算法中，当目标函数较复杂时，则每次对目标函数所计算时间过长，甚至用秒记录，因此对基本鱼群算法做如下改进［9－10］:种群中各个个体目标函数值只算一遍，且其下一状态的目标函数值也只算一遍，算完之后均记录下来以备后面使用，这种改进可使程序的运行时间得到较大的改善。通过改进的鱼群法在连续潮流中的应用如图2（a）、（b）所示。

图2（a） 裕度算法 图2（b） 改进人工鱼群算法

3 模态分析

在上述优化基础上，通过模态分析，可辨识在负荷极限时电压薄弱点，找到有效的校正控制点。从电压幅值与无功功率强耦合而与有功功率弱耦合可知，只考虑无功和电压的关系:

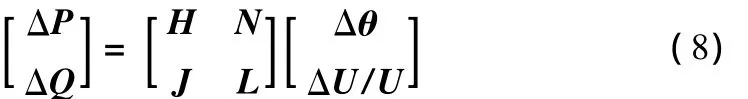
根据式（6）得到系统的电压无功线性化关系化模型:

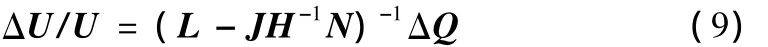
其中（L－JH－1N）－1为电压/无功灵敏度矩阵，它反映系统的电压与无功之间的变化关系，通过此矩阵的对角线元素的大小，可判断系统的薄弱。

4 算例分析

本算例是IEEE 14、IEEE 30节点电力系统。本文分别用CPF、基于CPF的基本人工鱼群法及改进人工鱼群法分别对系统以电压稳定裕度及电压偏移量最小为目标函数进行电压稳定分析，以所有PV节点电压，T1、T2、T3分接头及无功补偿装置装置C1、C2、C3为优化参数，在此基础上分析U－Q灵敏度识别系统在不同运行状态下的弱节点。仿真结果如表1、表2、图3、表3和表4所示。

表1 IEEE 14节点系统的稳定裕度

从表1、表2结果可知，本文基于CPF改进人工鱼群法得到的静态稳定裕度、电压偏移量有所改善，其临界点时，IEEE 14节点、IEEE 30节点系统稳定裕度值分别为 λ14lim=0.832、λ30lim=2.258，电压偏移值为:ΔU14=34.054、ΔU30=33.455，这是由于当控制变量变化时，电网结构发生变化，从而提高静态电压稳定性;且从表2可得，基于CPF的改进人工鱼群法寻优最佳代数小。

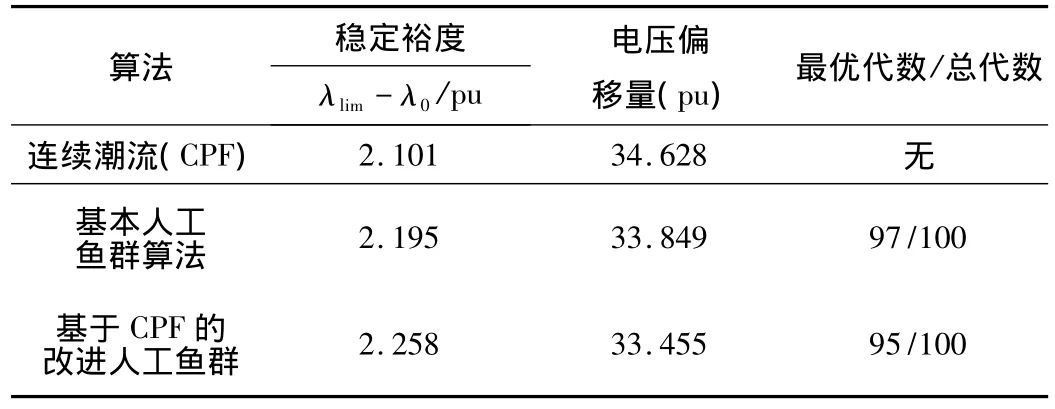
表2 IEEE 30节点系统的稳定裕度

图3（a）、（b）分别为IEEE 9、IEEE 30系统结构中负荷节点9、负荷节点3在不同算法中的λ－V图，随着负荷水平的增加，负荷节点电压相应地降低，直到电压崩溃点。由图3知，在同一工况下，基于CPF改进人工鱼群法的稳定裕度最大，改善了系统稳定性。这是由于对控制变量进行了优化，在崩溃点之前例如曲线1变为曲线2，电压值均增大，如λ=0.6时，节点电压由a点增大为b点，从而提高了稳定裕度。

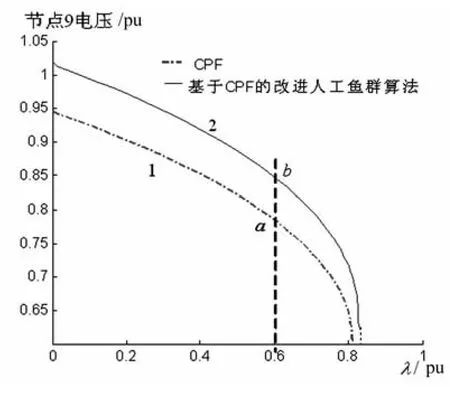
图3（a）IEEE14

图3（b）IEEE30

表3 PQ节点灵敏度指标

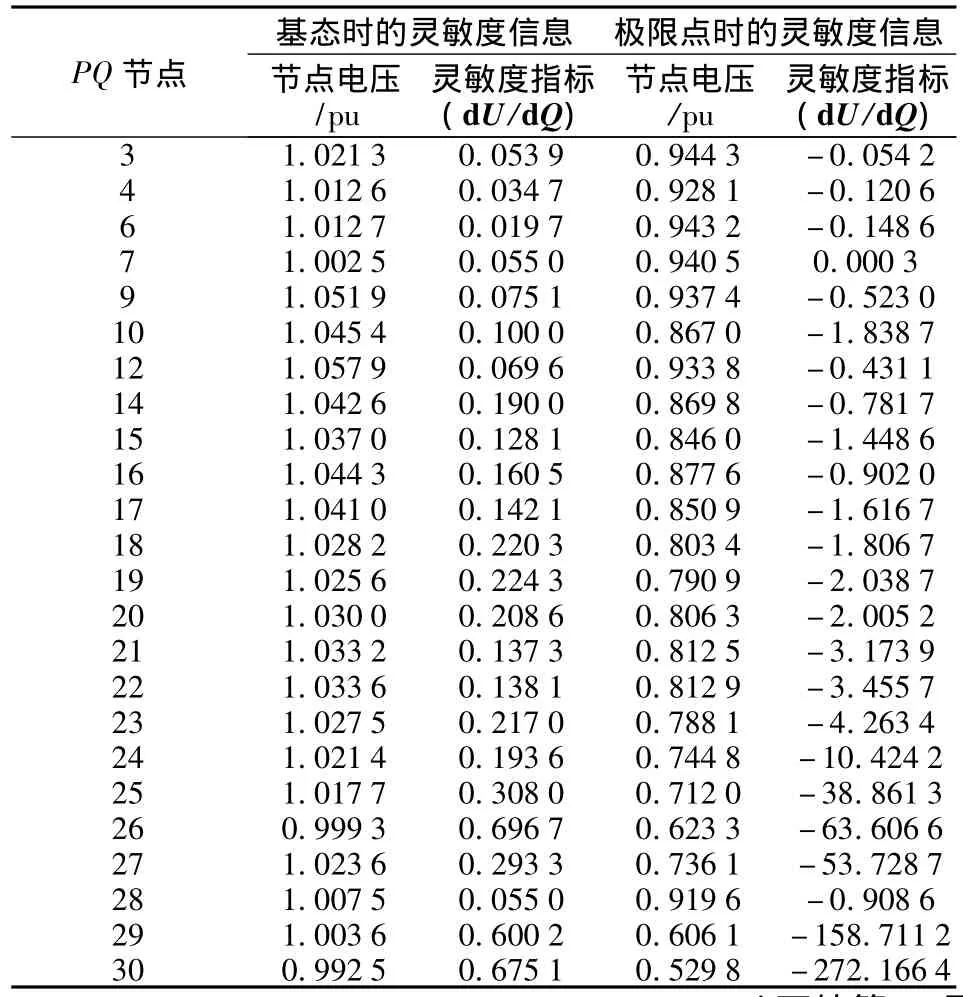
表4 PQ节点灵敏度指标

由表3得在dU/dQ信息中，基态时负荷节点都为正值，相对处于稳定状态;随着负荷水平的增加，在极限运行条件下灵敏度值全为负值，各节点都处于不稳定状态，不稳定程度依次为14、13、12、10、11、9、6、7、8、4、5、3 节点;根据 dU/dQ 信息，由表 4 同样可得各节点稳定排序。根据排序大小应预先对控制点采取相应的控制方式，以防事故扩散。

5 结束语

本文算法物理概念明确、收敛性好。基于CPF改进人工鱼群方法充分考虑了种群竞争优胜劣汰分布程度，有效地改善了寻优效率，并很好地克服了控制变量的离散性与连续性相混合难以处理的问题。采用文中的电压稳定分析方法计算结果表明:可有效求得系统最大负荷点，判断系统稳定裕度，模态分析方法可以定位电压稳定的薄弱区域，为控制措施的实施提供有效指导。

［1］周双喜，朱凌志，郭锡玖，等.电力系统电压稳定性及其控制［M］.北京:中国电力出版社，2004.

［2］张伯明，陈寿孙，严正.高等电力网络分析（第2版）［M］.北京:清华大学出版社，2007.

［3］胡彩娥.应用基于连续潮流算法的遗传算法进行静态电压稳定分析［J］.电网技术，2004，28（15）:57 －58.

［4］李增国，王锐，邢卫荣.基于连续潮流和模态分析的电压稳定分析［J］.电力自动化设备，2009，29（9）:82 －83.

［5］赵兴勇，张秀彬，何斌.优化有载调压变压器改善电压稳定性的新算法［J］.高 电压技术，2007，33（10）:170 －173.

［6］潘晓杰，刘涤尘，任冲，等.一种研究电压稳定的有载调压变压器模型［J］.高电压技术，2006，32（2）:21 －22.

［7］赵万明，黄彦全，谌贵辉.电压稳定静态分析方法综述［J］.电气开关，2009，47（1）:1 －3.

［8］胡彩娥.应用基于连续潮流算法的遗传算法进行静态电压稳定分析［J］.电网技术，2004，28（15）:57 －58.

［9］李晓磊.一种新型的智能优化方法－人工鱼群算法［D］.浙江:浙江大学，2003.

［10］王闯.人工鱼群算法的分析及改进［D］.大连:大连海事大学，2008.