哥德巴赫猜想证明中的误差问题

(中国城镇供热协会编辑出版部，北京 100026)

自笔者在文献[1]中提出一个对哥德巴赫猜想的证明后，有学者就其误差问题提出质疑。提出：文献[1]中有关素数及哥德巴赫猜想证明中的重要规律，即在我们针对某具体素数并用其去除奇数对的个数时，每该素数个奇数对，最多会有2个含有该素数的奇合数对(包括该素数本身。所谓“奇合数对”，是指一对奇数(相加后等于所论偶数的两个奇数)中，只要其中一个奇数是该素数或更多情况是含该素数的合数即可)，也就是最多有两个必须删去的奇合数对。这在整除时是精确的，或在相除后的整数部分是精确的。但用素数去除奇数对的个数时，由于通常不能整除，小数(或纯分数)部分会有误差。随着我们从小到大地对素数进行这种先除再删含该素数因子的奇合数对(也可以说是保留不含该素数的奇数对)，参与相除的素数不断增多，且不断增大。所以尽管通常误差会正负相消而趋于0，但也不能绝对地排除(起码还没有证明)极端情况下的误差累计越来越大，以至于最终威胁到这一证明的成立与否。比如，我们有23个奇数对，被素数5除，将得4又3/5。也就是整除部分为4，但还余3个奇数对。由于我们必须要在存在5个奇数对时才能确定肯定会有2个含5因子的合数对(含5本身)，现在只有3个奇数对，在这3个中，究竟是有1个含5因子的奇合数对，还是2个，还是没有，无法预先确定，也似乎无法在这种从小到大的操作过程中针对各种情况总结出规律性的东西。而且即使有规律，肯定也太复杂而不直观。还有一点必须说明的，我们在计算删去含素数5因子的合数对后，所剩余的奇数对的比例为(1-2/5)=3/5，如果原先的奇数对仍为23个，要求出确定值，不能23先乘以分子上的3再除以5，这样得到13又4/5，不对。不是13个为确定值，4个不确定。应该是23先除以5，得4又3/5，其意义是23个奇数对中，有如果5个一组，有4组，但还有3个奇数对不能成为一个完整的组。也就是前面说的无法一般性地确定究竟该删去几个(除非针对具体的偶数已经确定的情况，但这对我们的讨论没有意义，我们研究的是针对所有偶数的情况)，也就是说，经过先除5的操作后，我们可以确定肯定是可以留下4*3=12个奇数对的，还有3个无法确定究竟是否应该留下来。我们只能说，这3个奇数对能否留下来的概率，每一个是3/5。3个，就是3*(3/5)=9/5=(1又4/5)。这是一个概率的概念，是不确定的。

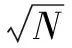
[1]

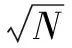
这个从大到小的删除(或保留)顺序，宗旨是越大的素数，可删除的奇合数对占总奇数对的比率越低，也就是可保留下来的奇数对越多，这样可以为对较小的素数进行删除(保留)操作提供“充足的数量空间”，明确说就是使剩下的奇数对足够多，以满足整除或除后得到的数有小数点前的整数部分，以致去掉小数后面的部分，也还能保证对下面更小的素数的同样的操作。

以上，通过简单、明确的说明，应该已经可以彻底澄清哥德巴赫猜想证明过程中的误差问题。其中从大到小地删除还是从小到大地删除，起着决定性的作用。当然，与“删除”相对应的，就是“保留”，我们删的是合数，留的是素数。沿此思路，其实我们完全还可以很好地解释[1]式的成立。这里不想占篇幅详细论述了，只提供一个思路：由于在[1]式中，小数点后面的小数(或整数部分后面的分数)表示的是一个概率，比如，5/7，表示此时还剩5个奇数对，但如果被素数7除，不够除的，所以无法确定究竟该如何决定5个奇数对的取舍。所以，每一个奇数对，它保留的概率是5/7。在[1]式中，由于所有这些素数的不能整除的分数部分是参与连乘的关系，所以概率是累积的。但实际上，由于我们是从最大的那个素数开始操作的，这个素数自乘(平方)，是小于该所论偶数的最大的奇数的，凡大于此数的，都会大于该偶数而不予考虑了，因此，所谓该删的含该素数的奇合数，它含有的其它素数，只能比这个素数小。也就是会在删比这个素数小的奇合数是被删掉。同时我们前面已经证明，按这种操作方法，都会有整数部分，因此实际保留下来的素数对，应该只能比[1]式中含概率意义的下的素数对多，因此[1]式完全成立。总的原则和思路，是先删除含可能的最大的素数组成的奇合数对，由于这个素数大，所以那个含有它的奇合数对占总奇数对的比率必低，可删的少；另一方面，也就是说可保留的奇数对必多，下面再去对更小的素数操作时，可以保证能够逐次删掉余下的含较大素数的奇合数对。而如果先从小的素数操作起，结论就比较模糊了。这个思路理解起来要复杂一些，这里只是提一下，由于哥德巴赫猜想已经可以由前面的方法证明了，所以对这个证明的理解就不是很重要了。读者可以略去。

至此，笔者在文献[1]中对哥德巴赫猜想的证明过程中的误差问题，应该得到了很好的说明，同时本身也是一个更确切的证明。它彻底地排除了误差问题的困扰，无任何悬念地证明了哥德巴赫猜想。

本文请对照文献1阅读。可看成是文献[1]的一个补充，也可看成是一个补充证明。

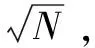
最后，笔者再次强调，如果所有奇数对的个数可以被相关素数整除，[1]式中连乘的每一个分式项的含义，就不是概率性的，而是实实在在的比例关系。比如，3/5，就意味着每5个奇数对中，就有3个不含素数5为因子的奇数对。这里是确定的数目，不是概率为3/5。但是如果不能整除，最后可能有误差(充其量少算2个奇数对)，那么，考虑这个因素后，我们不妨就把连乘式[1]中的每一个分数项，看成概率，而且是对整个奇数对的个数域都成立的概率。当然这完全不必要。因为概率部分只涉及不能整除的小数部分，也就是未能整除后剩下的那几个奇数对才存在究竟还应在这几个奇数对中删除几个(最多2个)或不删的问题。前面的整除部分(小数点左边)删除与保留的数目都是确定的。比如我们有3002个奇数对，其中没有素数3因子的确定的奇数对有3000乘以1/3为1000个，而其它2个不确定，要看具体情况，但其没有素数3因子的概率是1/3。但显然，这两个奇数对与1000相比只占很少比例，而且随奇数对数目的增加(随哥德巴赫猜想中所取偶数的越来越大)，所占比例(误差)显然会越来越少。但尽管如此，我们还是可以把概率看成对全域成立，而不仅仅是余数部分的。其原因是，所谓概率，就是随样本的越多，其准确率越高，误差越低。因此，在所取偶数足够大时，误差完全可以忽略不计，即使对全域而言也是如此(更何况只涉及很少奇数对的非整除部分(分数或小数点后的数))。在这个意义上，[1]式完全可以成立，本文的这几个为了追求更为确定的非概率结果的“补充证明”或“说明”，其实并不是必不可少的。唯一的目的，也就是想让整个证明完全非概率化以增加确定性而已(代价是，在满足哥德巴赫猜想的前提下，删除了很多其实不必删除的素数对)。

最后，再补充两点说明：1、本文中的公式[1]中，由原先的分母都是素数的分数的连乘，加进了分母为奇合数的纯分数(分式值小于1的)连乘，其在公式中的作用其实使剩下的素数对实际上更少了，因此即使如果有误差的话，此足以抵消它们。2、文献[1]中的“引理1”实际与艾拉托色尼筛法实际是一回事。引理[1]实际当然是艾拉托色尼筛法可以进行下去的基础。

参考文献：

[1]沈卫国.若干重要数论问题的证明[J].天津职业院校联合学报，2011，(11).