基于预插黏性界面单元的Koyna重力坝强震破坏过程分析

徐海滨，杜修力，杨贞军

（1．北京工业大学 城市与工程安全减灾教育部重点实验室，北京 100124；2．浙江大学 建筑工程学院，杭州 310058）

强震作用下的坝体开裂过程模拟对于大坝抗震安全分析具有重要意义。目前有两种模拟混凝土坝体损伤开裂的数值分析方法得到了重视和快速的发展，一种是从断裂力学的角度出发，研究大坝的断裂响应。从宏观角度来看混凝土是一种准脆性材料，易发生脆性断裂，适于采用断裂力学方法。如Skrikerud等［1］和Ayari等［2］用离散裂缝模型分析大坝的动力开裂和闭合。Bhattacharjee等［3］和 Calayir等［4］用改进的弥散裂缝模型—旋转裂缝模型在考虑非正交裂纹的影响下，对Koyna重力坝进行了动力开裂分析。方修君等［5］对质量矩阵进行了修正，将扩展有限元法应用于动态断裂问题的求解，对Koyna重力坝进行了地震响应分析。杜效鹄等［6］在分析中引入黏聚裂纹模型，并对重力坝模型的复合开裂过程进行了模拟。另一种为基于连续介质损伤力学的裂缝计算模型。Cevera等［7］建立了各向同性损伤模型，研究了Koyna重力坝在地震作用下的损伤破坏情况。Yazdchi等［8］用有限元与边界元相互结合的方法分析了Koyna坝的缩尺模型在地震作用下坝体的损伤发展。

但是离散裂缝模型和弥散裂缝模型都不同程度地存在着网格敏感性。弥散裂缝模型由于缺乏不连续的位移模式，在网格边界不与主应力方向平行时非常容易产生应力锁死现象。扩展有限元法（XFEM）是美国西北大学Belytschko等［9］首先提出来的，XFEM引入非连续的阶跃函数来表征裂缝两侧的非连续位移场，不需要网格重分，但是该方法裂纹贯穿单元需要改变裂纹单元的积分格式，且程序实现很复杂、难度较大。损伤力学的裂缝模型只是将断裂过程视为一个损伤积累的过程，不能直接描述裂缝的开裂和扩展的过程。

近年来，黏性裂缝模型（Cohesive Crack Model，CCM）受到学者们的持续关注并发展迅速［10］，这种较成熟的模拟裂缝扩展的模型提出了在裂缝尖端存在一个过渡区（Fracture process zone），假定在这个区域中存在内聚力（法向、切向或者混合），以此来分担集中于尖端的应力，从而避免在解有限元方程过程中的奇异问题，而且可以高效简便地在各种数值计算方法中得以实现，如有限元和离散元等。Yang、Su等［11－13］开发了在实体有限元网格中灵活插入黏性界面单元的算法和程序，对混凝土轴心受拉试件进行了二维和三维复杂随机断裂的蒙特卡罗模拟，随后又对四个典型的混凝土静态和动态三维断裂例子进行模拟，验证了此方法模拟断裂的可行性。

本文基于黏结裂缝模型的模拟方法，在通用有限元软件ABAQUS平台上，将文献［11］中所开发的二维算法和程序，扩展运用到混凝土重力坝在强震作用下的断裂破坏研究中，以Koyna重力坝为研究对象，对混凝土重力坝的断裂破坏过程和宏观力学性能进行研究，探索其破坏机制。

1 黏性裂缝模型

20世纪50年代末，Barenblatt［14］和 Dugdale［15］首先提出适用于金属延性材料的黏结裂缝模型，然后Hiller-borg等［16］提出适用于混凝土等材料的虚拟裂缝模型。黏结裂缝模型和虚拟裂缝模型开启了对断裂过程区中的能量进行数值模拟。黏结裂缝模型在断裂过程区内考虑：骨料咬合作用、裂缝面间的摩擦作用和材料的黏结作用。这些作用在数学模型中表示为：一个垂直裂缝面的拉应力tn和裂缝平面内的剪应力ts，而且考虑应变软化作用，也就是说，随着裂缝面相对法向位移δn和切向位移δs的增大，相应的应力逐渐减小。这种应力随着裂缝面相对位移的增大而减小的规律，可用应力－相对位移曲线表示，如图1所示：在弹性阶段，裂缝并未出现，应力随着相对位移的增大而线性增大；在软化阶段，当应力达到起裂水平，材料开始软化，软化曲线与坐标轴包围的面积称为材料的Ⅰ型断裂能Gf和Ⅱ型断裂GfII。需要说明的是，由于混凝土的抗压强度远比抗拉强度大，因此，在裂缝的法向应力－相对位移曲线（图1）中，当应力为负，即为压应力时，不存在应变软化。断裂能与黏结强度的关系如式（1）所示

式中：t0为黏结强度，δsep为开口位移，G为断裂能

这就决定了每个裂缝单元的极限位移为

1．1 弹性阶段

单元顶面和底面受到的应力与其相对位移满足线性关系：

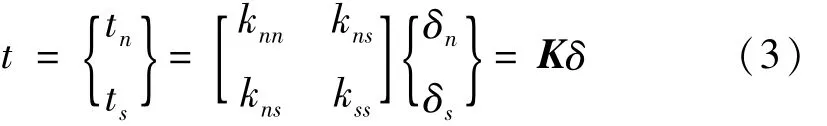
式中：t为两个方向上的应力分量，tn裂缝面法向应力，ts为裂缝面内的剪应力。δ为对应的位移分量。K为单元的刚度矩阵，在通常的数值模拟中，一般取对角线外数值为零。

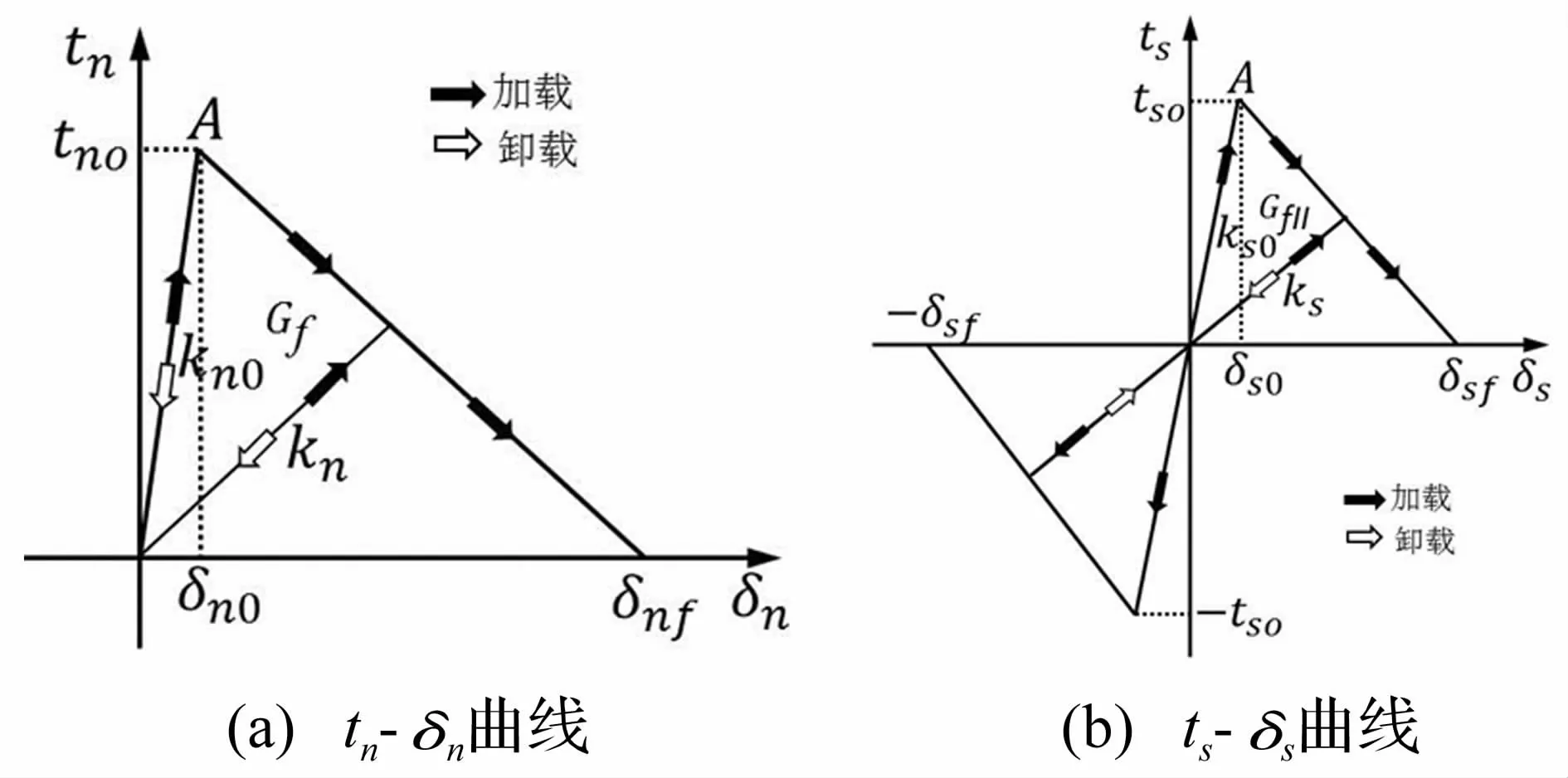
图1 Cohesive单元的应力－相对位移关系［11］Fig．1 The stress-relative displacement relationship of cohesive element

1．2 软化阶段

进入软化阶段后，裂缝单元出现损伤，由于材料的损伤单元的刚度将减小。损伤变量D介于0～1之间，它是一个计算变量，后处理中用SDEG表征，其又是有效相对位移δm的函数：

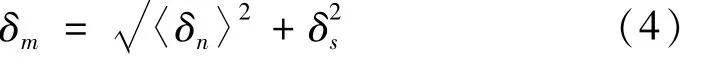
〈〉是Macaulay括号：

如图1中的线性软化准则，损伤指标如下：

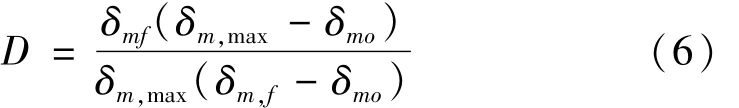
其中：δm，max是加载历史中的最大有效相对位移。δmo和δmf分别是裂缝起裂和完全破坏时的有效相对位移。

用初始刚度knn和kss表示退化后的刚度kn和ks：

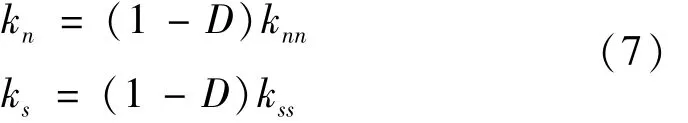
应力为：

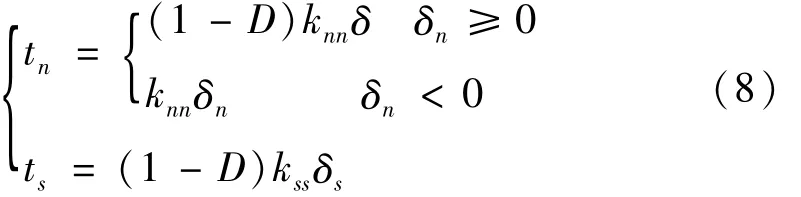
本文采用名义应力平方准则为起裂准则，其表达式如下：

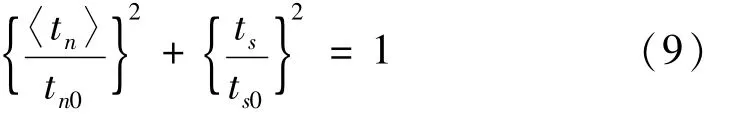
其中：tn0、ts0分别为各个方向单独作用的起裂应力。

2 嵌入黏性界面单元 CIEs（Cohesive Inter-face Elements）

本文的模拟方法是将裂缝单元嵌入各实体单元边界上［11］，对初始有限元网格进行处理，图2为嵌入裂缝单元前后的有限元网格以及裂缝单元的示意图，需要说明的是，插入的裂缝单元在几何上厚度为零，为了示意裂缝位置，在图中显示为带一定厚度的单元。

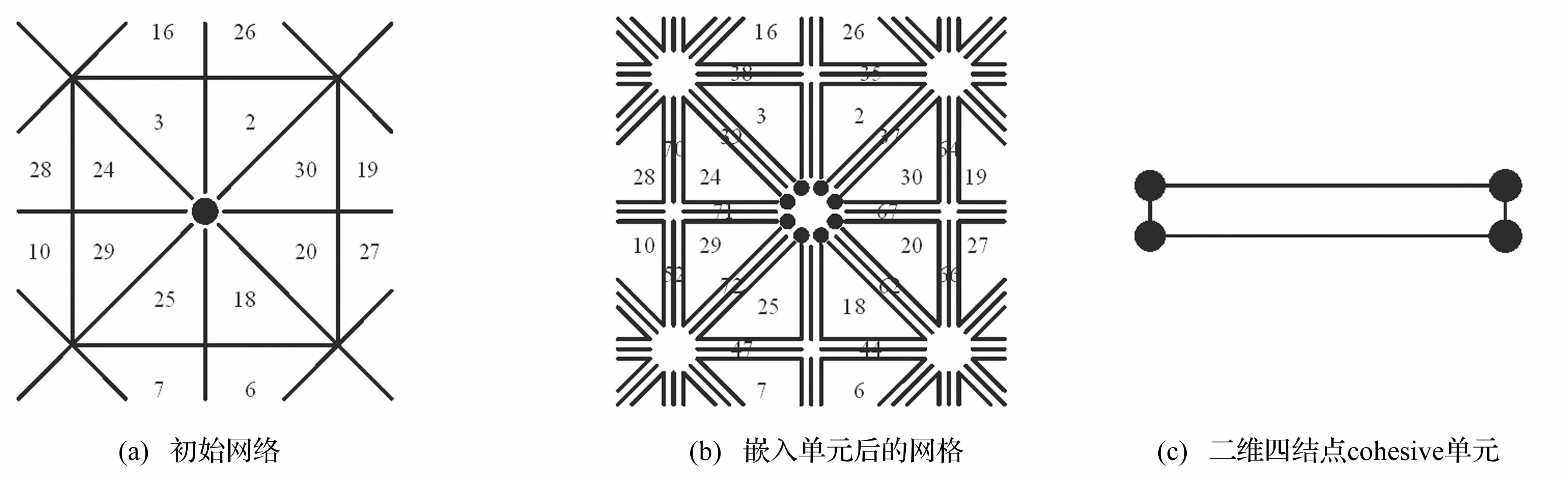
图2 嵌入cohesive单元前后网格示意图Fig．2 Inserting cohesive elements in the initial mesh

3 算例验证

Du等［17］开展了承受冲击荷载的三点混凝土加载梁。试件的几何尺寸和边界条件见图3，三点加载梁在梁顶面中点位置受到冲击荷载作用，在底面中点位置有一个12．7 mm的预制缺口。试验中测到的冲击荷载（见图4）作为本次模拟的外部荷载，施加在作用点上。试件的混凝土弹模E＝34 480 MPa，泊松比 ν＝0．2，密度 ρ＝2 500 kg／m3。根据 Du等［17］的建议，本文采用如图5所示的极数软化曲线表示为混凝土的软化属性，其断裂能为152 N／m。

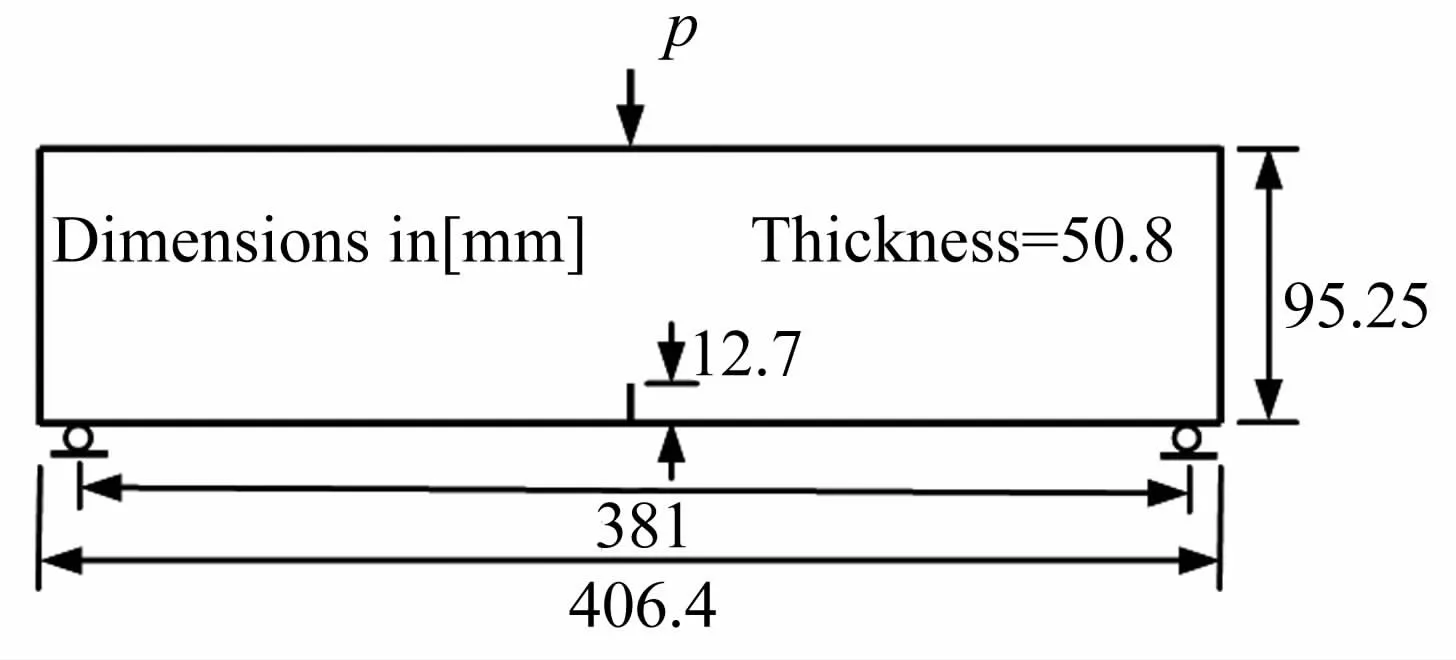
图3 三点加载梁的几何尺寸和加载条件Fig．3 Impact test of a concrete beam

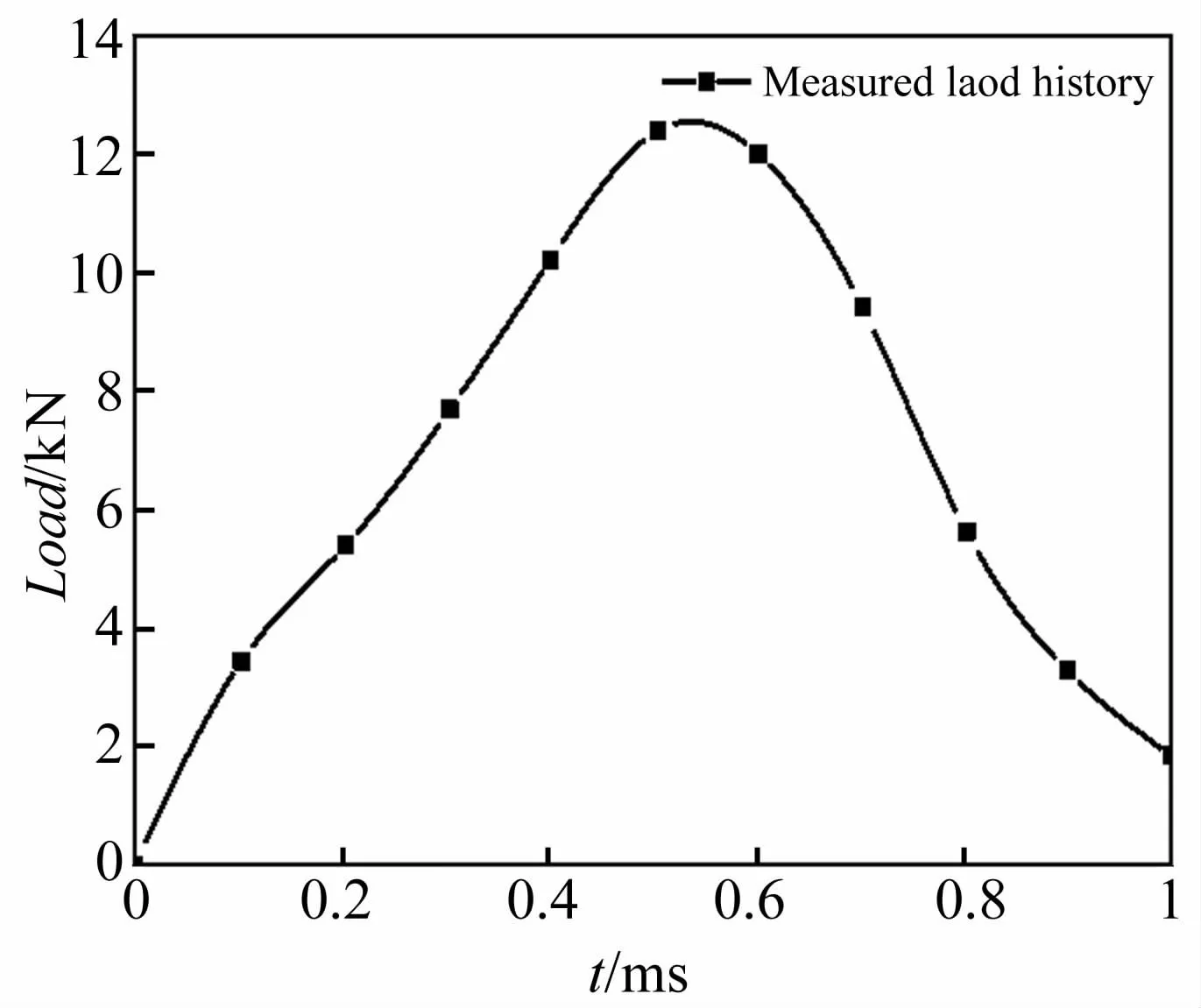
图4 试验测得的冲击荷载曲线Fig．4 Load history used for the impact test

由于该三点加载梁结构和边界条件关于中轴对称，荷载位于中轴线上，因此，裂缝将沿着试块的中轴线展开。基于以上考虑，本次模拟中，只在裂缝开展路径上嵌入裂缝单元。图6为荷载加载完毕时，有限元网格的变形图。其中红色单元为已经开裂的裂缝单元，损伤指标（SDEG）均大于0．99。

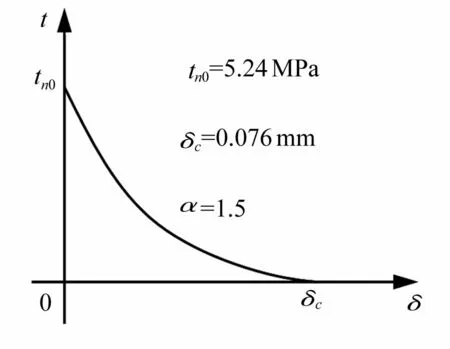
图5 三点加载梁采用的软化曲线Fig．5 Exponential softening law for the impact test

图6 三点加载梁受冲击荷载后断裂形态Fig．6 Deformed mesh for the impact test

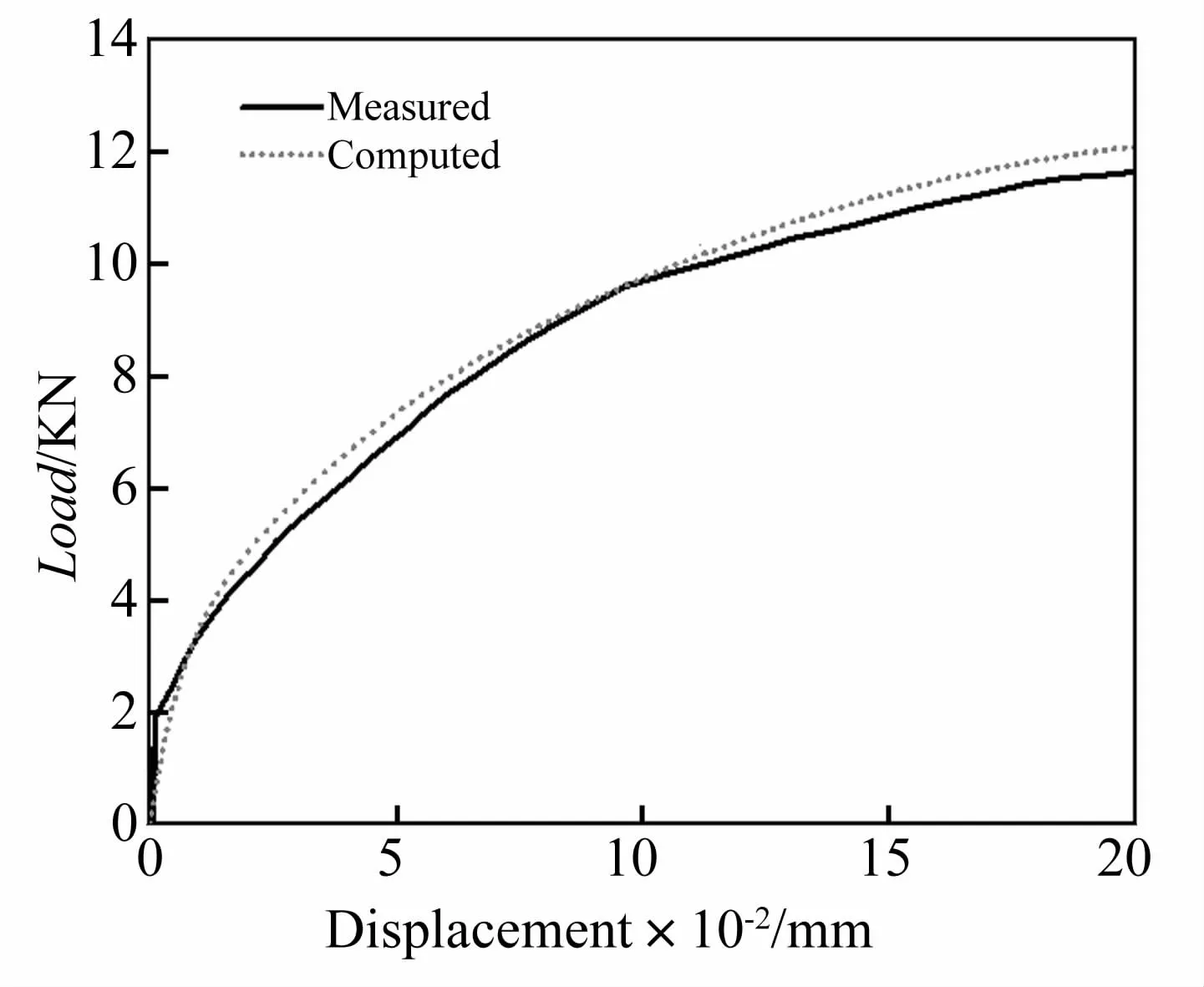
图7 三点加载梁的荷载－位移曲线比较Fig．7 Load-displacement curves for the impact test

图7 为本次模拟所得荷载－位移曲线和试验测得的曲线。从图中可以看出，两者在初始阶段吻合的较好，在末端稍有差别，但偏差不大。另外，提取了裂缝尖端位置随时间的变化曲线，其中裂缝尖端是指损伤指数（SDEG）介于0．99上下的两裂缝单元共用结点处。图8为模拟结果与试验测得的裂缝尖端的发展历程，试验中只得到三个时间点的裂缝尖端位置，从比较可见，模拟结果与试验数据以及苏项庭等三维模拟结果［13］均较吻合。

图8 裂缝尖端的位置变化比较Fig．8 Crack-tip extension history for the impact test

4 Koyna重力坝强震破坏分析

Koyna重力坝作为少数几个在强震中破坏且有较完整记录的重力坝之一，为混凝土重力坝动力分析常用典型大坝。Koyna大坝位于印度的Koyna河上，坝高103 m，坝顶宽度 14．8 m，坝底宽70 m，坝段厚16 m，在坝高66．5 m处，下游坝面的坡面发生突然改变。1967年该坝坝址区域遭受一次6．5级强烈地震作用，在91．75 m高的库前水位和0．474 g水平和0．312 g的竖向加速度峰值地震作用下，坝体发生开裂，并在裂缝处发生渗漏。坝体混凝土材料弹性模量 E＝31 027 MPa，μ＝0．15，ρ＝2 463 kg／m3，动态拉伸屈服强度 σt＝2．9 MPa，抗压强度 σc＝24．1 MPa，断裂能 250 N／m，Rayleigh阻尼因子根据线弹性分析得到的前两阶频率计算。

计算模型如图9所示，取Koyna最大坝高坝段为研究对象（坝高103 m），地面实测地震波如图10所示。本文对重力坝模型划分了粗细两套网格，有限元模型采用三角形单元，实体单元边界上均嵌入黏性裂缝单元，如图11所示。粗网格含有6 336个结点和1 858个裂缝单元，细网格含有13 707个结点和3 577个裂缝单元。

图9 Koyna重力坝模型尺寸Fig．9 Koyna gravity dam model

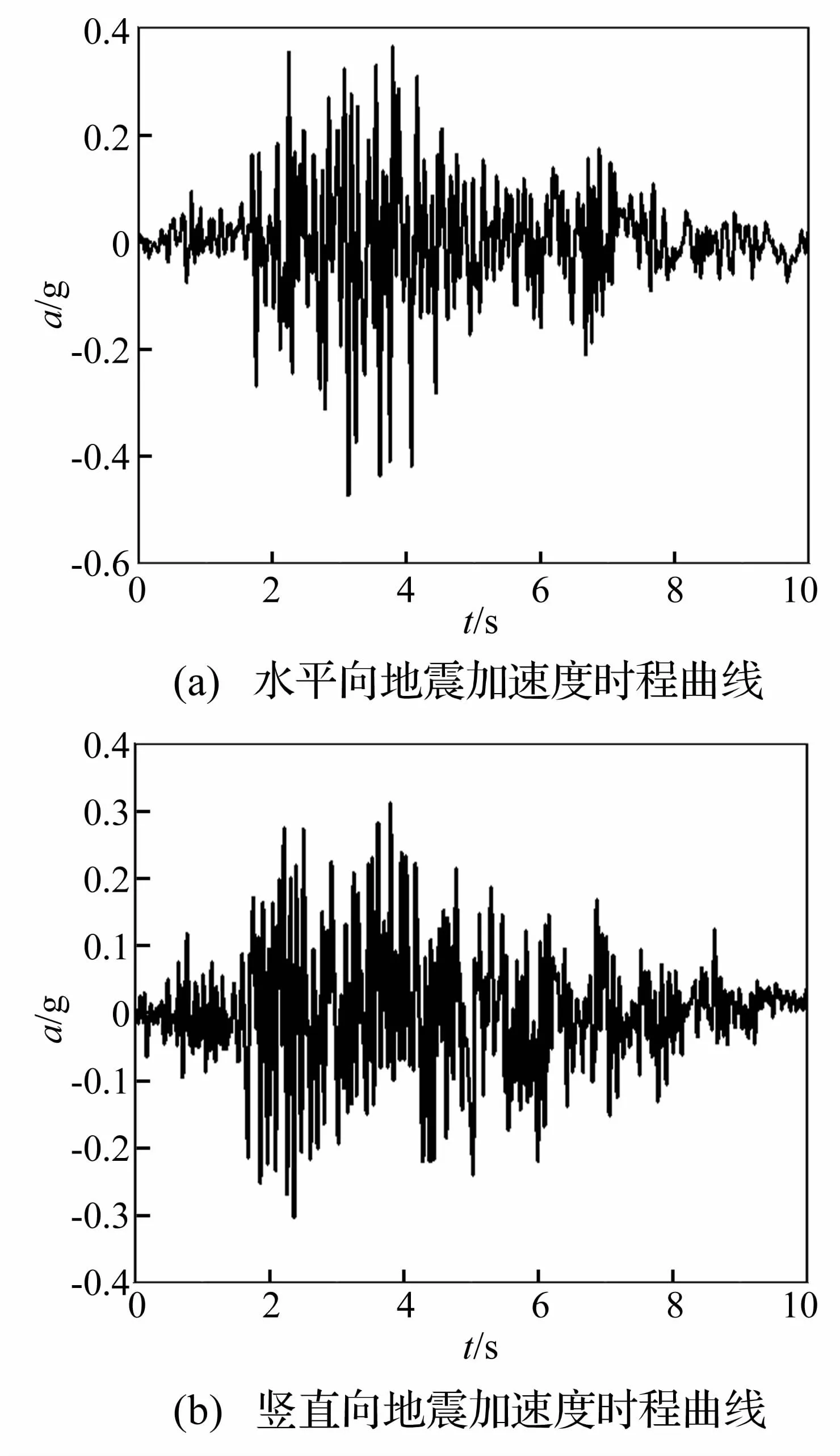
图10 Koyna地震地面加速度记录Fig．10 Seismic acceleration records of Koyna

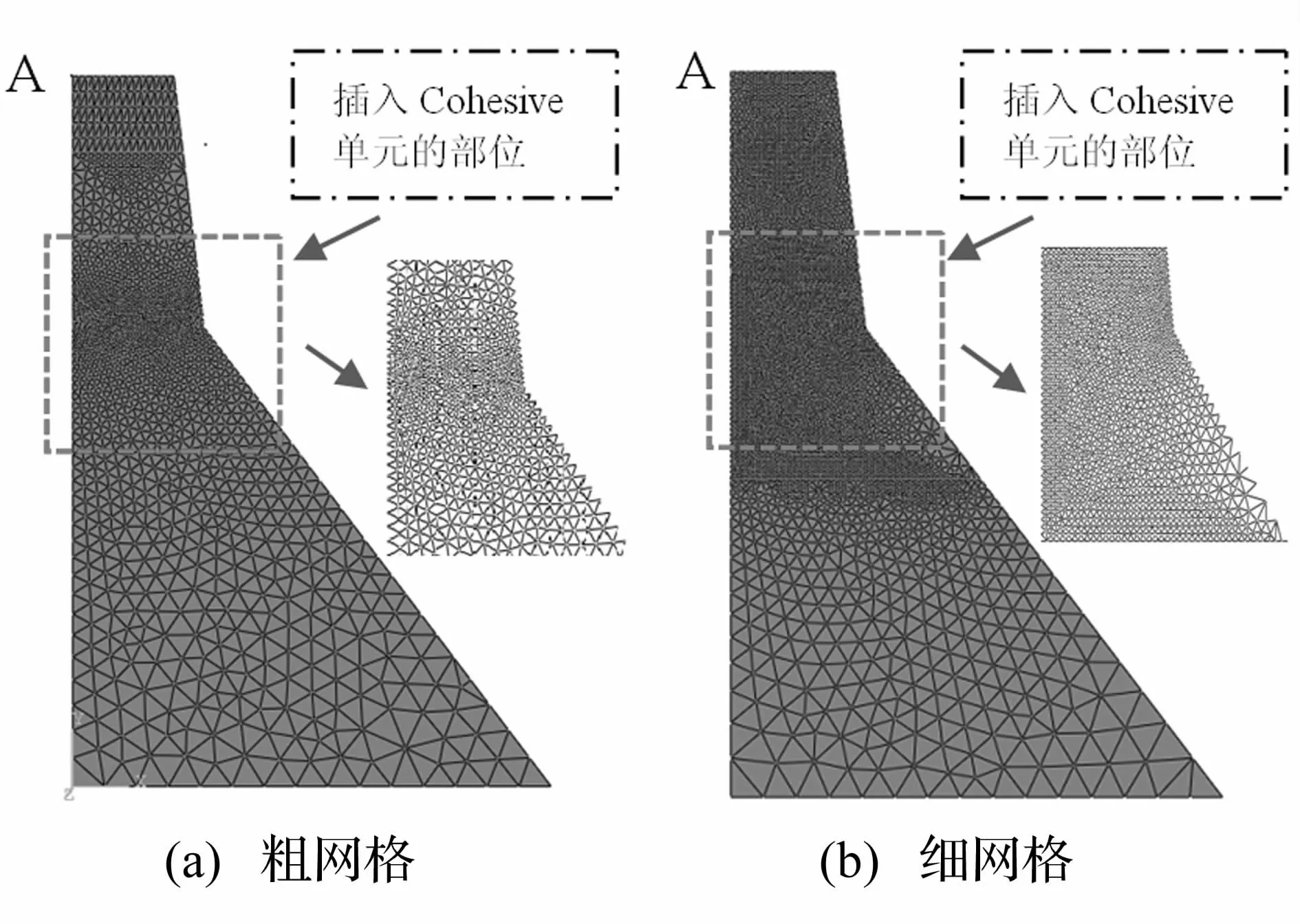
图11 有限元模型及插入的cohesive单元模型Fig．11 Finite element model and inserting cohesive elements

基于黏结裂缝模型理论，在坝体实体单元边界处插入cohesive单元，采用名义应力平方准则，得到Koyna实测地震波作用下的大坝最终破坏模式。图12和图13是Koyna重力坝在地面强震作用下断裂和扩展的过程，裂缝的动态开展过程主要是靠SDEG（Scalar Dam-age Variable）来表征单元的破坏程度，SDEG是一个无量纲量，大小从0到1，开裂的裂缝单元均为损伤指标（SDEG）大于0．99。从图12中可以看出裂纹从坡度突变处最先萌生并以一定角度斜向坝体内部扩展，主裂缝逐渐发展为两条，一条主裂缝沿着水平向扩展，最终扩展至上游面形成贯穿性裂缝；另一条主裂缝仍旧沿着一定角度斜向上游面扩展形成贯穿性裂缝；同时两条主裂缝周边衍生出许多微裂纹。图13得到的前期裂缝发展轨迹与图12非常相似，只是斜向的裂缝没有形成贯穿，但是发展趋势是一样的，这个主要是裂缝局部化导致的，粗细网格的划分导致插入裂缝单元的密度不同，扩展路径稍有不同，但趋势是相似的，可见此模型具有一定的网格依赖性，但是网格依赖性不大。

图12 Koyna重力坝的断裂扩展过程（粗网格）Fig．12 The fracture extension process of Koyna gravity dam（coarse mesh）

图13 Koyna重力坝的断裂扩展过程（细网格）Fig．13 The fracture extension process of Koyna gravity dam（fine mesh）

图14 坝顶水平位移响应Fig．14 The horizontal displacement response of dam crest

图14 和图15为两套网格在地震作用下坝顶A点的水平和竖向位移响应，由于大坝在2．5 s左右时完全断裂，所以位移时程只有2．5 s。水平向位移响应前段吻合的很好，后面稍有差别，但是趋势一样。竖向位移响应整体吻合的很好。由此也可以看出本方法的网格依赖性不大。

图15 坝顶竖向位移响应Fig．15 The vertical displacement response of dam crest

图16 为Koyna重力坝的几种断裂破坏形态，图（a）为Lee等［18］提出的混凝土塑性损伤模型，并依此对Koyna大坝进行了地震反应分析，得到坝体损伤结果；图（b）为张社荣等［19］基于扩展有限元法（XFEM）对Koyna重力坝地震破坏过程进行分析，得到的大坝开裂破坏分布；图（c）为振动台试验的结果［20］；图（d）、（e）为本文方法得到的模拟结果。通过比较可以看出，本文方法得到的最终断裂破坏形态，其中斜向的主裂缝与图（a）、（b）、（c）基本一致，水平向贯穿主裂缝与图（a）描述的基本一致，说明采用cohesive单元可以较好地模拟大坝在强震作用下的失效模式。

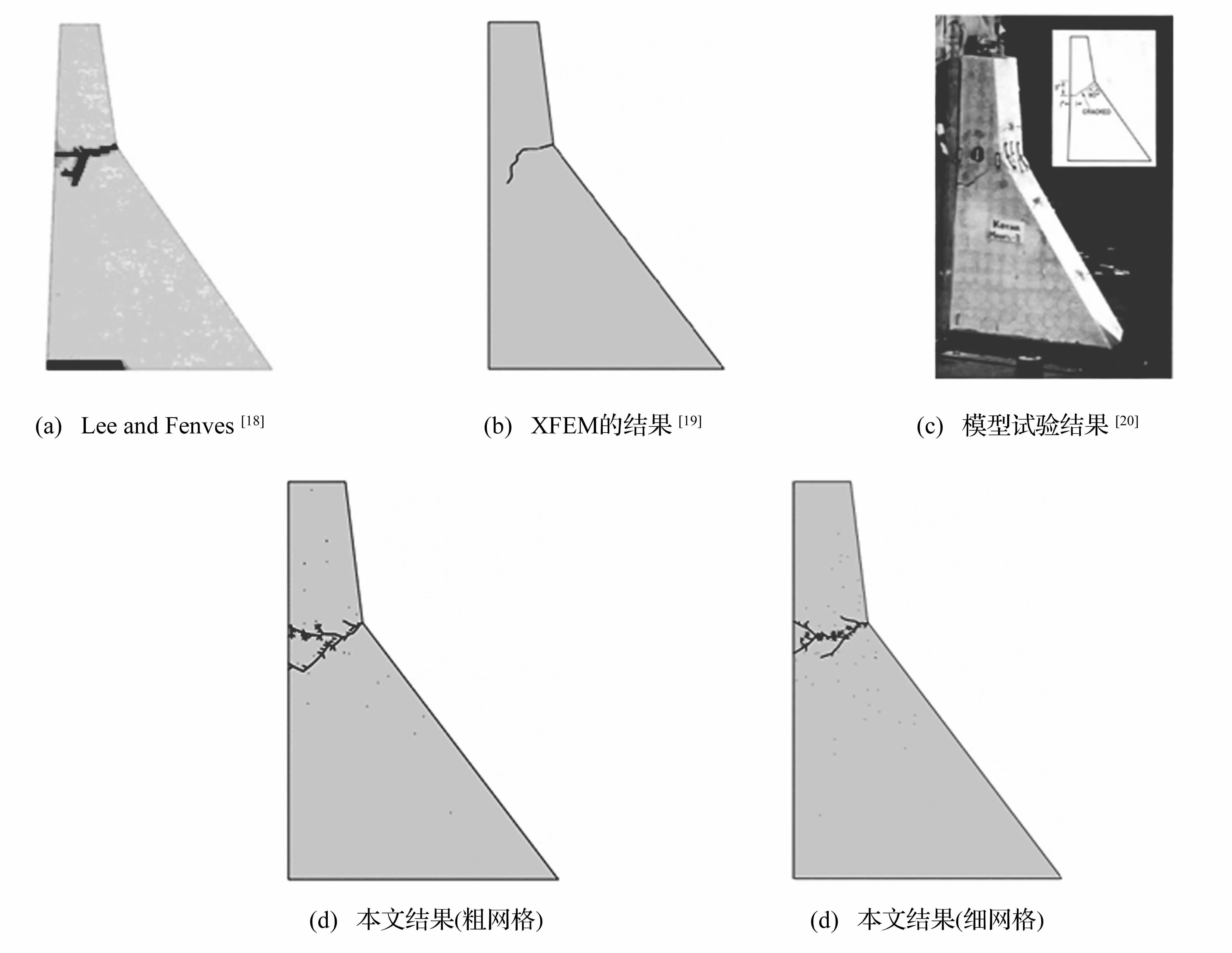
图16 Koyna重力坝断裂破坏形态Fig．16 Fracture failure patterns of Koyna gravity dam

5 结 论

本文基于黏性裂缝模型理论，在坝体实体单元边界处插入黏性界面单元，对Koyna重力坝在强震作用下的破坏过程进行数值模拟，得到的地震破坏模式与实际震害、损伤破坏、扩展有限元破坏和模型试验基本一致，说明采用黏性界面单元可较好地描述裂缝的起裂和扩展，能直观地模拟大坝在强震作用下动力破坏过程。本文的优势在于不需预设开裂路径，避免了网格重划分，但是预插的黏性界面单元，增加了自由度的数目，计算效率是个值得关注的问题，有待于和其他方法进行比较。

［1］Skrikerud P E，Bachmann H．Discrete crack modeling for dynamically loaded，unreinforced concrete structures［J］．Earthqu．Engng．Struct．Dynam，1986，14：297－315．

［2］Ayari L M，Saouma V E．A fracture mechanics based seismic analysis of concrete gravity dams using discrete cracks［J］．Engng．Fract．Mech，1990，35：587－598．

［3］Bhattacharjee S S，Leger P．Seismic cracking and energy dissipation in concrete gravity dams［J］．Earthqu．Engng．Struct．Mech，1993，22：991－1007．

［4］Calayir Y，KaratonM．Seismic fracture analysis of concrete gravity dams including dam-reservoir interaction［J］．Comput．Struct，2005，83：1595－1606．

［5］方修君，金峰，王进廷．基于扩展有限元法的Koyna重力坝地震开裂过程模拟［J］．清华大学学报（自然科学版），2008，48（12）：2065－2069．FANG Xiu-jun，JIN Feng，WANG Jin-ting．Seismic fracture simulation of the Koyna gravity dam using an extended finite element method［J］．Joumal of Tsinghua University（Science and Technonlogy）．2008，48（12）：2065－2069．

［6］杜效鹄，段云岭，王光纶．重力坝断裂数值分析研究［J］．水利学报，2005，36（9）：1035－1041．DU Xiao-hu， DUAN Yun-ling， WANG Guang-lun．Numerical analysis of fracture in gravity dam［J］．Journal of Hydraulic Engineering，2005，36（9）：1035－1042．

［7］Cevera M，Oliver J，Faria R．Seismic evaluation of concrete dams via continuum damage models［J］． Earthquake Engineering and Structural Dynamics．1995，24（9）：1225－1245．

［8］Yazdehi M，Khalili N，Valliappan S．Non-linear seismic behaviour of concrete dams using coupled finite element-boundary element technique［J］．International Journal for Numerical Methods in Engineering，1999，44：101－130．

［9］Belytschko T，Black T．Elastic crack growth in finite element with minimal remeshing［J］． International Journal for Numerical Methods in Engineering，1999，45（5）：610－620．

［10］Shet C，Chandra N．Analysis of energy balance when using cohesive zone models to simulate fracture processes［J］．Journal of Engineering Materials and Technology Transaction of the ASME．2002，124，440－450．

［11］Yang Z J，Su X T，Chen J F，et al，Monte Carlo simulation of complex cohesive fracture in random heterogeneous quasi-brittle materials［J］．International Journal of Solids and Structures，2009，46（17）：3222－3234．

［12］Su X T，Yang Z J，Liu G H，Monte Carlo simulation of complex cohesive fracture in random heterogeneous quasi-brittle materials：A 3D study［J］．International Journal of Solids and Structures，2010，47（17）：2336－235．

［13］Su X T，Yang Z J，Liu G H，Finite element modelling of complex 3D static and dynamic crack propagation by embedding cohesive elements in abaqus［J］．Acta Mechanica Solida Sinica，2010，23（3）：271－282．

［14］ Barenblatt G I．The formation of equilibrium cracks during brittles fracture： general ideas and hypothesis， axially symmetric cracks［J］．Applied Mathematics and Mechanics，1959，23：622－636．

［15］Dugdale D S．Yielding of steel containing slits［J］．Journal of the Mechanics and Physics of Solids，1960，8（2）：100－104．

［16］Hillerborg A，Modeer M，Petersson P E．Analysis of crack formulation and crack growth in concrete by means of fracture mechanics and finite elements［J］．Cement and Concrete Research，1976，6：773－782．

［17］Du J，Yon J H，Hawkins N M，et al．Fracture process zone for concrete for dynamic loading［J］．ACI Materials Journal，1992，89（3）：252－258．

［18］Lee J，Fenves G L．A plastic-damage concrete model for earthquake analysis of dams［J］．Earthquake Engineering＆Structural Dynamics．1998，27（9）：937－956．

［19］张社荣，王高辉，孙博，等．基于扩展有限元法的重力坝强震潜在失效模式分析［J］．水利学报，2012，43（12）：1431－1439．ZHANG She-rong，WANG Gao-hui，SUN Bo，et al．Seismic potential failure mode analysis of concrete gravity dam based on extended finite element method［J］．Journal of Hydraulic Engineering，2012，43（12）：1431－1439．

［20］National Research Council． Earthquake engineering for concrete dams：design，performance，and resaerch needs［M］．National Academics Press，USA，1990：99－100．