水下和空中爆炸时混凝土重力坝动态响应对比分析

张社荣，孔 源，王高辉

（1．天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2．武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072）

水工大坝由于其显著的政治经济效益，一直是局部战争或恐怖袭击的重点攻击对象。然而大坝一旦失事，将对下游造成巨大的灾难和损失，大坝安全防护一直是国家总体安全战略的重要组成部分。在恐怖袭击及意外爆炸事件中，大坝可能遭受来自火箭弹、空投炸弹和洲际导弹的空中爆炸袭击，也可能遭受来自鱼雷、水雷和潜射导弹的水下爆炸袭击。然而由于水和空气的物理属性差异以及与爆炸产物的界面作用效应不同，冲击波在水和空气中的传播特性存在较大的差异；进而导致大坝在水下和空中爆炸冲击波荷载作用下的动态响应及破坏特性存在较大差异。因此对比研究水下和空中爆炸冲击荷载作用下大坝动态响应对大坝结构的抗爆防护设计具有重要意义。

爆炸荷载下的结构动态响应是一个复杂的物理过程，它是由炸药的起爆过程、爆炸冲击波在介质中的传播过程、介质与结构相互作用及结构响应四个过程组成的。相同药量的炸药，在水或空气中爆炸时，产生的冲击波的传播特性有所差异，同时结构物的动态响应也不一样。如Rajendran等［1］综述了炸药在水下和空中爆轰及其产生的爆炸冲击波传播的特点、爆炸冲击波荷载作用下金属薄板的塑形变形与断裂破口及相应的数值模拟等方面的研究成果，表明水下爆炸冲击波的强度及其对结构的破坏能力均比空中爆炸冲击波强。宁心等［2］采用试验的方法对比研究了水下和空中爆炸冲击波传播速度和物理参数，表明，相较于空中冲击波，水下冲击波具有压力峰值高、正压持续时间短和冲量较大的特点。Kwak等［3］对比研究了在水下和空中时爆炸产物膨胀过程和爆炸冲击波传播过程。Clut-ter等［4］利用爆炸流体动力计算程序预测了设备在水下和空中爆炸两种不同冲击波荷载作用下的脆弱性评估。Librescu等［5］运用数值方法对比研究了各向异性夹层平板在水下和空气中爆炸冲击波荷载作用下的动力响应，发现平板在水下爆炸时破坏程度更严重。黄建松等［6］对比分析了水下和空中爆炸对船员的冲击损伤效应。张社荣等［7－8］通过构建重力坝水下爆炸全耦合模型，探讨了大坝在水下爆炸时可能的破坏模式及相应的破坏机制；同时构建了重力坝侵彻爆炸、库前水中爆炸和库区近空爆炸的全耦合模型，探讨了混凝土重力坝在不同爆炸方式下的可能破坏模式及抗爆性能。但由于问题的复杂性，关于水下和空中爆炸冲击荷载作用下混凝土重力坝的动态响应的对比研究甚少。

文中通过构建自由场水下和空中爆炸耦合模型，研究了爆炸冲击波在水和空中两种介质中的传播特性，并与相应的经验公式进行对比分析，验证了数值计算的可靠性。同时考虑炸药的起爆、冲击波传播、冲击波与结构的相互作用以及结构的动态响应等复杂过程，通过构建水下和空中爆炸全耦合模型，对比分析混凝土重力坝在水下和空中爆炸荷载作用下的动态响应，可为混凝土重力坝的抗爆设计和防护提供参考。

1 动力损伤模型及材料模型

1．1 混凝土动力损伤模型

由德国 EMI的 Riedel等［9－10］研究提出的 RHT本构模型是在HJC本构模型的基础上发展而来的。它包含了三个失效面，即屈服失效面、最大失效面和残余失效面，如图1所示，分别代表混凝土的初始屈服强度、峰值失效强度及峰后残余强度。故该模型在考虑了混凝土的大应变、高应变率、高压效应的同时，还兼顾了应变硬化、软化和应力偏量第三不变量的影响，能很好地描述高应变率条件下混凝土的响应问题。

屈服面Yfail是由标准化压力p*，偏应力面上罗德角θ和应变率ε·的方程决定的：

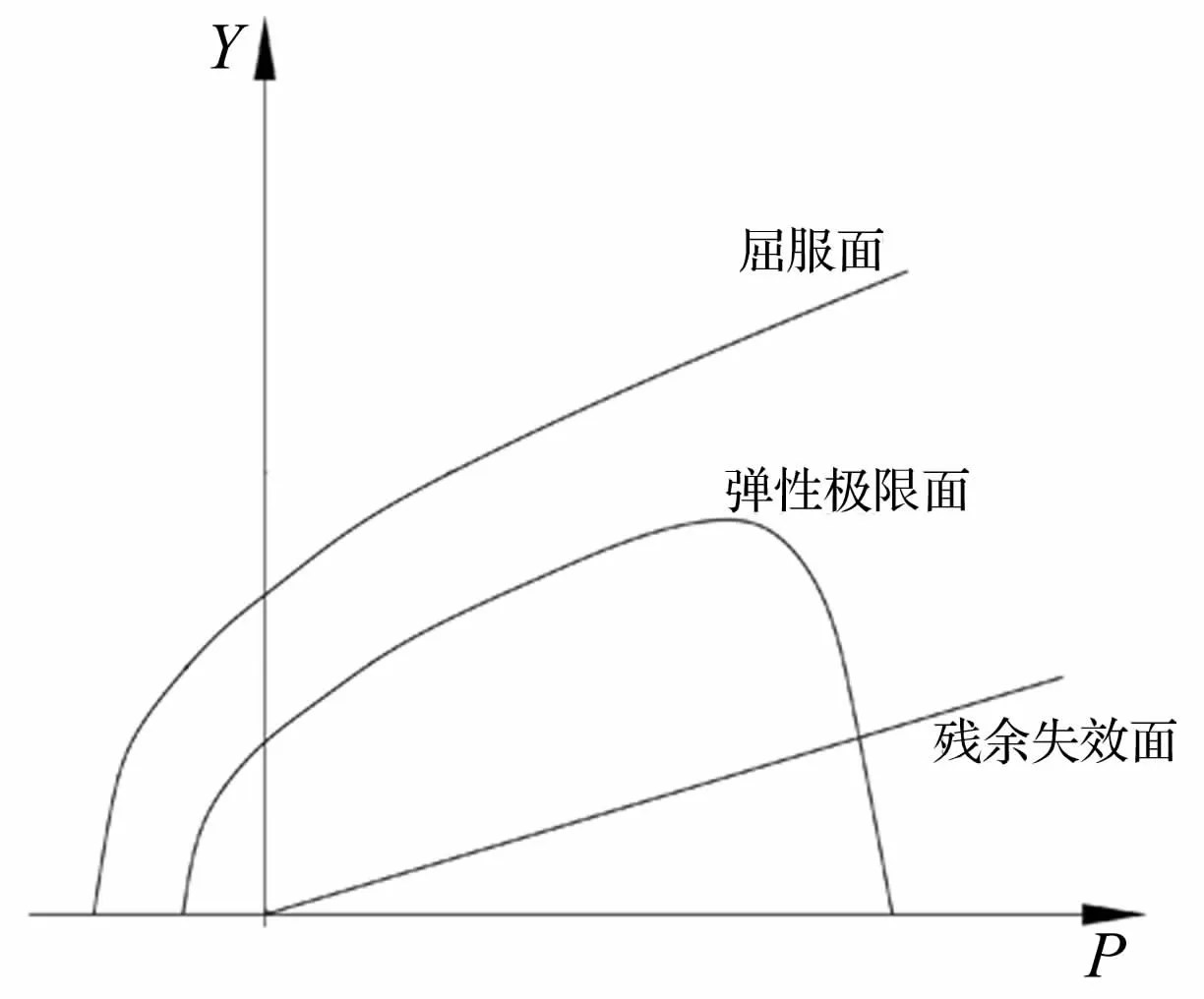
图1 三个强度面Fig．1 Three strength surface

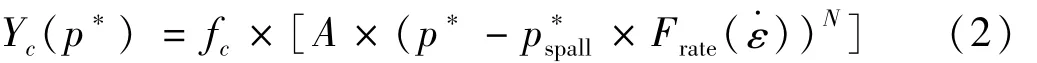
其中，受压子午线为：式中：fc是混凝土单轴抗压强度，为3．5×107Pa；A、N为材料模型参数，分别为1．6和0．61；p*＝p／f为标准化

c的静水压力；p*spall＝ft／fc＝0．1，ft为混凝土单轴抗拉强度；Frate（·ε）为应变率·ε相关的动力放大系数；r3（θ）为标准化的最小包络面到静水压力轴的矩离，可表示为：

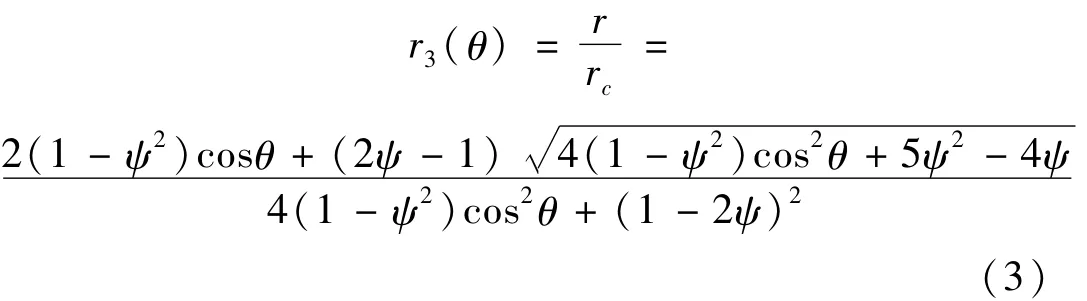
式中：ψ＝rt／rc，rt、rc分别为静水压力轴到拉伸、压缩子午线的距离；罗德角θ是应力偏量第二、三不变量的函数，可由下式计算得到：

弹性极限面Yelastic：

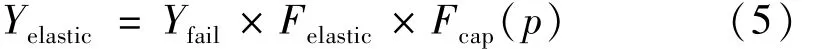
式中：Felastic是弹性强度与失效面强度之比，一般取常数，Fcap（p）是盖帽函数，用于限制静水压下的弹性偏应力。

当前屈服面介于弹性极限面与失效面之间：

式中：εpl塑性应变，εpl（pre－softening）与当前时步等效塑性应变增量相关。

残余失效面

式中：B为残余失效面常数，M为残余失效面指数。B＝0．7，M＝0．8。

RHT本构模型的损伤定义为：

式中为损伤常数，分别为 0．015和 1．0；Δεpl为等效塑性应变增量；为最小失效应变，设为0．000 8。

1．2 基岩动力损伤模型

采用由Johnson等［11］研究提出的JH－2本构模型模拟基岩在爆炸荷载下的力学行为。

材料未发生损伤（D＝0）时，JH－2本构模型中材料的状态方程可表示为

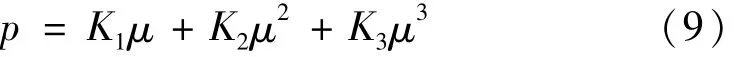
式中：p为静水压力，K1为材料的体积模量，K2、K3为材料常数，μ为体应变，μ＝ρ／ρ0－1（ρ为当前密度，ρ0为初始密度）。各参数取值如下：K1＝2．57×1010Pa，K2＝－4．5×1012Pa，K3＝3×1014Pa，ρ0＝2．66×103kg／m3。

材料开始发生损伤（D＞0）后，会发生膨胀，因此在多项式后加入修正项Δp。

JH－2强度模型是将材料的等效应力表示成静水压力的幂函数形式，并且与应变率和损伤因子D相关，其中定义的标准化的强度模型为

当材料未发生损伤（D＝0）时，标准化的等效应力可表示为：

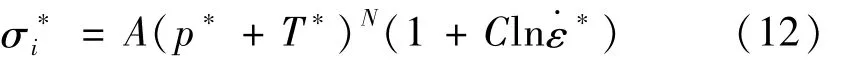
当材料完全破碎（D＝1）时，标准化的等效应力可表示为：

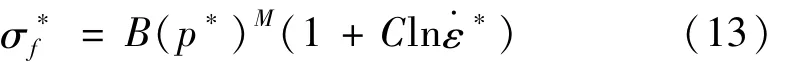
式中：A、B、C、M和 N是材料常数，p*为标准化的静水压力，T*为标准化的材料能承受的最大静水拉应力，为标准化的应变率。各参数取值如下：A＝0．76，B＝0．25，C ＝0．005，M＝0．62，N＝0．62。

损伤变量D可表示为：

式中：Δεp是单次循环内的有效塑性应变的积分，ε是在一定压力下材料的破碎塑性应变，＝D1（p*＋T*）D2，D1和 D2是常数，分别为 0．005和 0．7，p*和 T*如式（12）。

1．3 材料模型及状态方程

高能炸药材料采用JWL状态方程［12］描述了爆轰压力P和每单位体积内能E及相对体积V的关系：

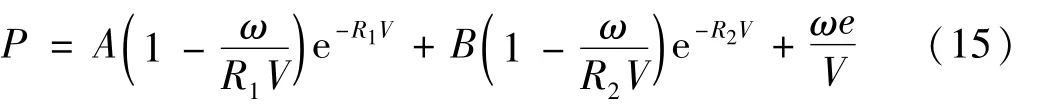
式中：P为爆轰产物的压力；V为爆轰产物体积和炸药初始体积之比；e为炸药的初始内能；A、B、R1、R2、ω为特征参数，各参数取值如下：A＝3．738×1011Pa，B＝3．747×1011Pa，R1＝4．15，R2＝0．9，ω＝0．35，D＝6．93×103m／s，e＝5．999×109J／m3，PCJ＝2．10×1010Pa，ρ0＝1．63×103kg／m3。

水介质采用多项式状态方程［12］进行描述，其形式由根据压缩状态的不同而定。

当水为压缩状态（μ＞0）时，其状态方程为：

当水为膨胀状态（μ＜0）时，其状态方程为：

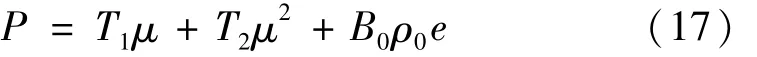
式中：μ＝ρ／ρ0－1，ρ0是初始密度；A1、A2、A3、B0、B1、T1和T2是由AUTODYN材料库直接赋值的常数；e是比内能，其定义式如下：

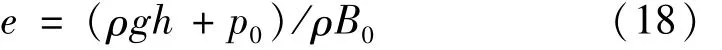
其中：ρ和h分别是水的密度和深度，g和p0分别是重力加速度和大气压强。各参数取值如下：ρ0＝1×103kg／m3，A1＝2．2×109Pa，A2＝9．54×109Pa，A3＝1．457×1010Pa，B0＝0．28，B1＝0．28，T1＝2．2×109Pa，T2＝0 Pa。

空气采用 Mat-Null材料模型和理想气体状态方程［12］：

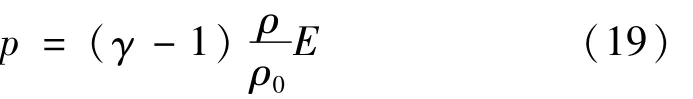
式中：E是比内能，γ是绝热指数（取1．4），ρ0是空气初始密度（取 1．225 kg／m3），ρ是当前密度。

2 全耦合数值模型

水下爆炸是一个复杂的过程，涉及炸药的起爆、冲击波传播、冲击波与结构（或自由面）的动态相互作用以及随后结构的动态响应等过程。在描述水下爆炸冲击波结构动态响应中，主要有欧拉（Euler）和拉格朗日（Lagrange）算法。欧拉算法中，自由边界面和材料的交界面通过固定的欧拉网格来表达，材料可通过固定的网格边界流进流出，故大变形或者有流动的情形不会导致网格畸变，适合于描述液体和气体的行为，但由于必须采用复杂的算法来追踪材料的运动，计算效率较为低下。拉格朗日算法中每个网格单元的顶点随填充材料一起移动，填充材料始终保持在原单元内而不会在单元之间流动，能很好的描述固体材料的行为，且与其他算法相比计算速度较快，但会因为物体大变形导致的网格畸变而使得计算精度下降甚至计算难以为继。在数值仿真模拟流固耦合问题及大变形问题时，可将欧拉单元和拉格朗日单元耦合以获得两种算法的优点，即耦合的欧拉 －拉格朗日算法（CEL算法）［13－14］。该算法的一般策略是把欧拉网格看作是拉格朗日网格的压力边界条件，把拉格朗日网格看作是欧拉网格的速度边界条件，如图2所示。

图2 欧拉－拉格朗日耦合算法示意图Fig．2 Schematic of the coupling Eulerian-Lagrangian approach

2．1 压力边界条件

CEL算法中，拉格朗日网格和欧拉网格两者的边界是重合的。每一个拉格朗日网格边界的片段都被认为是独立的，且分割成一组子单元，其中每一个子单元都被定义成分割欧拉网格的片段的一部分。流体作用在结构上使结构产生的内力等于作用在子片段中心处的应力和它的面积的乘积，作用在结构边界上的流体里的一般分布在两个拉格朗日节点上。

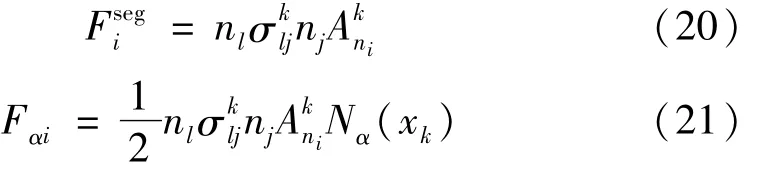
式中：k为第k个单元；Ak为第k个子单元的面积；N为边界的法向。

2．2 速度边界条件

流固耦合相互作用的问题，一般流体的运动幅度都比较大，因此流体域中使用欧拉算法描述，而在流体－结构的交界面上每个点处需设置两个节点，即流体节点和固体节点［15］。界面上每个点处的两个节点分别属于各自的物体。在流固交界面上的两个物体可以沿切向滑动、互相粘结或者互相脱离，其界面上对应节点的速度关系分别是法向速度相等、物质速度相等和速度相互独立。

3 自由场水下和空中爆炸冲击波传播特性的差异

由于水和空气的物理属性差异以及与爆炸产物的界面作用不同，爆炸冲击波在水和空气中的传播特性存在较大差异。为了研究水下和空中爆炸冲击波的传播特性，本文利用轴向对称性建立了自由场水下和空中爆炸的八分之一计算模型，对自由场水下和空中爆炸冲击波传播过程进行模拟。其计算模型如图3所示，计算区域为10 m×10 m×10 m，计算网格尺寸为100 mm。球形TNT装药量为1 000 kg，起爆点位于炸药的中心。炸药爆炸伴随着高温高压及物态的变化而变化，但其是在数值计算中的物质运动而网格不动，因此，水、空气和炸药均采用Euler算法以便对空间内每一点的物理量及其变化进行考察，同时可克服炸药爆炸所带来的网格畸变问题。为了模拟自由场水下和空中爆炸，在模型截断边界处施加Transmission无反射边界条件（该边界可模拟爆炸冲击波在截断边界处的透射现象，达到利用有限模型区域模拟无限域的目的。），使得冲击波在人工截断边界处透射出去。

图3 自由场爆炸计算模型Fig．3 Computational model of free-field explosion

图4 给出了爆心距5 m处的水下和空中爆炸冲击波典型压力时程曲线。由图4（b）可知，以标准大气压为界，空气压力时程曲线分为了正压区和负压区，当空中爆炸冲击波传播到目标计算点时，压力由标准大气压瞬间攀升到峰值，随后指数衰减到标准大气压，接着进入负压区，以逐渐降低的速度继续衰减。由图4（a）可知，当水下爆炸冲击波传播到目标计算点时，压力变化规律与空中爆炸压力时程曲线的正压区压力变化规律相似，瞬间攀升到峰值，随后呈指数衰减，衰减速度逐渐降低。爆心距5 m处，水下爆炸峰值压力是空中爆炸的39．62倍。

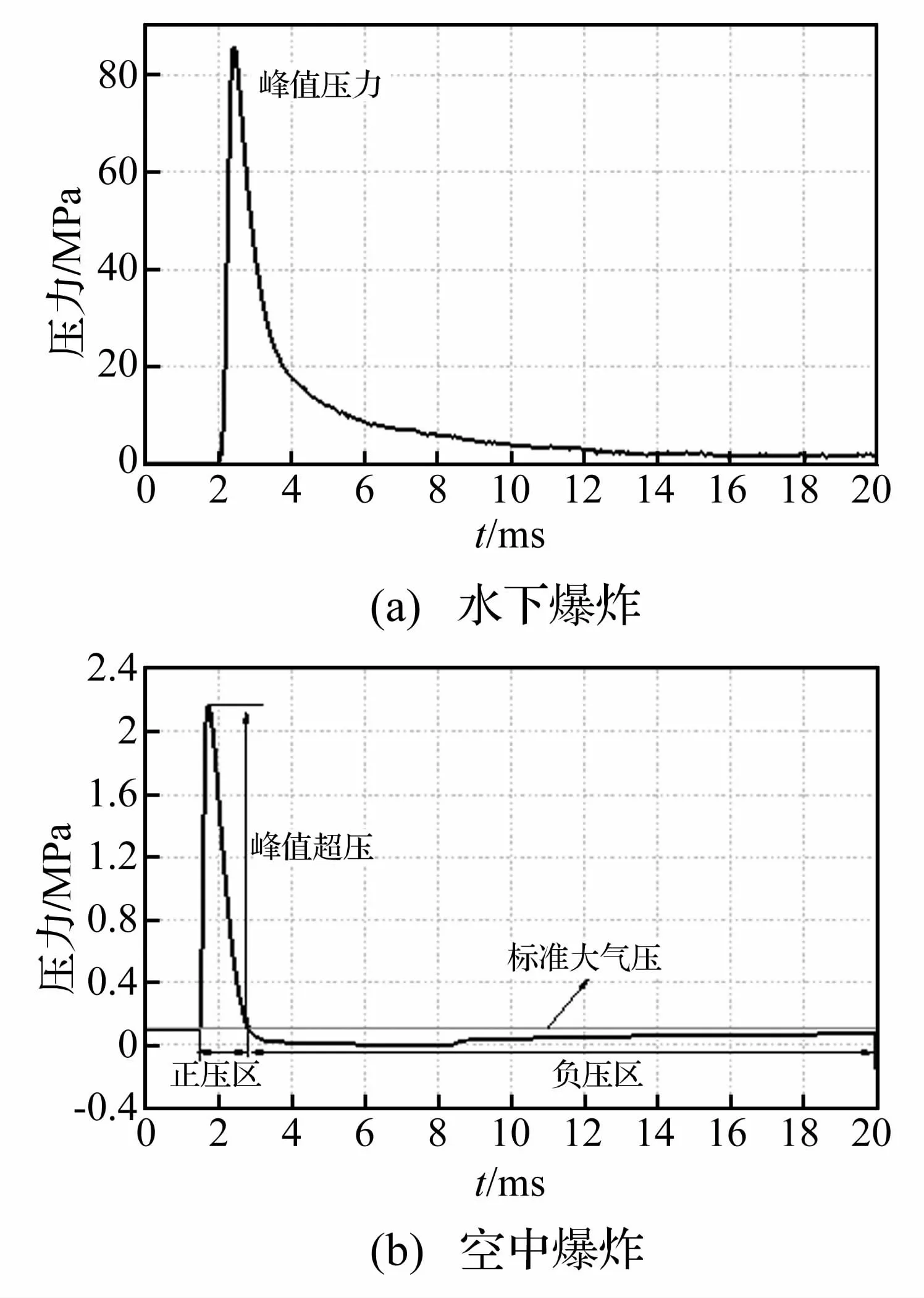
图4 爆心距5 m处的压力时程曲线Fig．4 Typical free pressure time history at 5 m from charge center

图5 给出了水下和空中爆炸冲击波传播的峰值压力和冲量对比。首先把数值模拟的计算值与经验公式［16－17］的经验值进行对比，在近爆区域，计算值与经验值存在一定差异，这是由较大的试验测量误差导致的；而随着爆心距的增大，计算值与经验值较接近，说明了数值模拟技术具有可靠性。由图5（a）可知，在爆心距相同的计算点处，水下爆炸峰值压力远大于空中爆炸，水下爆炸冲击波峰值平均压力是空中爆炸下的42．35倍（经验平均比值为32．65）；冲击波压力在空气中衰减较快，主要是由于相较于密度大、压缩性较小的水（通常认为是不可压缩的流体），空气具有密度小、可压缩性大的特点，故而冲击波在空气中传播时能量大量且快速地耗散在空气中。由图5（b）可知，在距炸药中心相同距离处，水下爆炸冲击波冲量远大于空中爆炸，水下爆炸冲击波平均冲量是空中爆炸下的72．00倍（经验平均比值为78．17）。综上所述，水下爆炸冲击波的压力峰值和冲量均较空中爆炸大得多。

4 不同爆炸方式下混凝土重力坝的动态响应对比分析

4．1 数值模型

取重力坝非溢流坝段为研究对象，坝高75 m，计算区域如图6所示，为减少计算耗时，可利用几何模型的对称性只建立二分之一的模型，该计算模型共有302 257个单元。模型包括大坝、基岩、TNT炸药、库水和空气共5种物质的耦合。爆炸瞬间，爆炸物质在有限的空间和极短的时间内释放出大量的能量，产生的反应产物具有高温高压的特点，且迅速挤压周围介质，使之发生大变形及流动现象；坝体及基岩离起爆点有一定距离，爆炸冲击波的破坏能力有所降低，两者的变形较小。故TNT炸药、库水和空气采用Euler网格，可拥有较好的精度；大坝和基岩采用Lagrange网格，可提高计算效率；库水和空气与大坝和基岩之间采用CEL算法。装药中心单元尺寸为100 mm，单元尺寸随着爆心距的增加而逐步增大。坝体的上部，控制单元尺寸为200 mm，单元尺寸朝着坝底的方向而逐步增大。水下爆炸深度及坝体上游面的爆心距均设为10 m，立方体形TNT装药量为1 000 kg。研究水下爆炸时，库前区域上部5 m为空气，下部70 m为水；研究空中爆炸时，库前区域75 m全为空气。为了研究坝体上的动态响应，分别在大坝上游面、下游面及坝顶设置计算点（计算点1＃、2＃和3＃，如图7）。

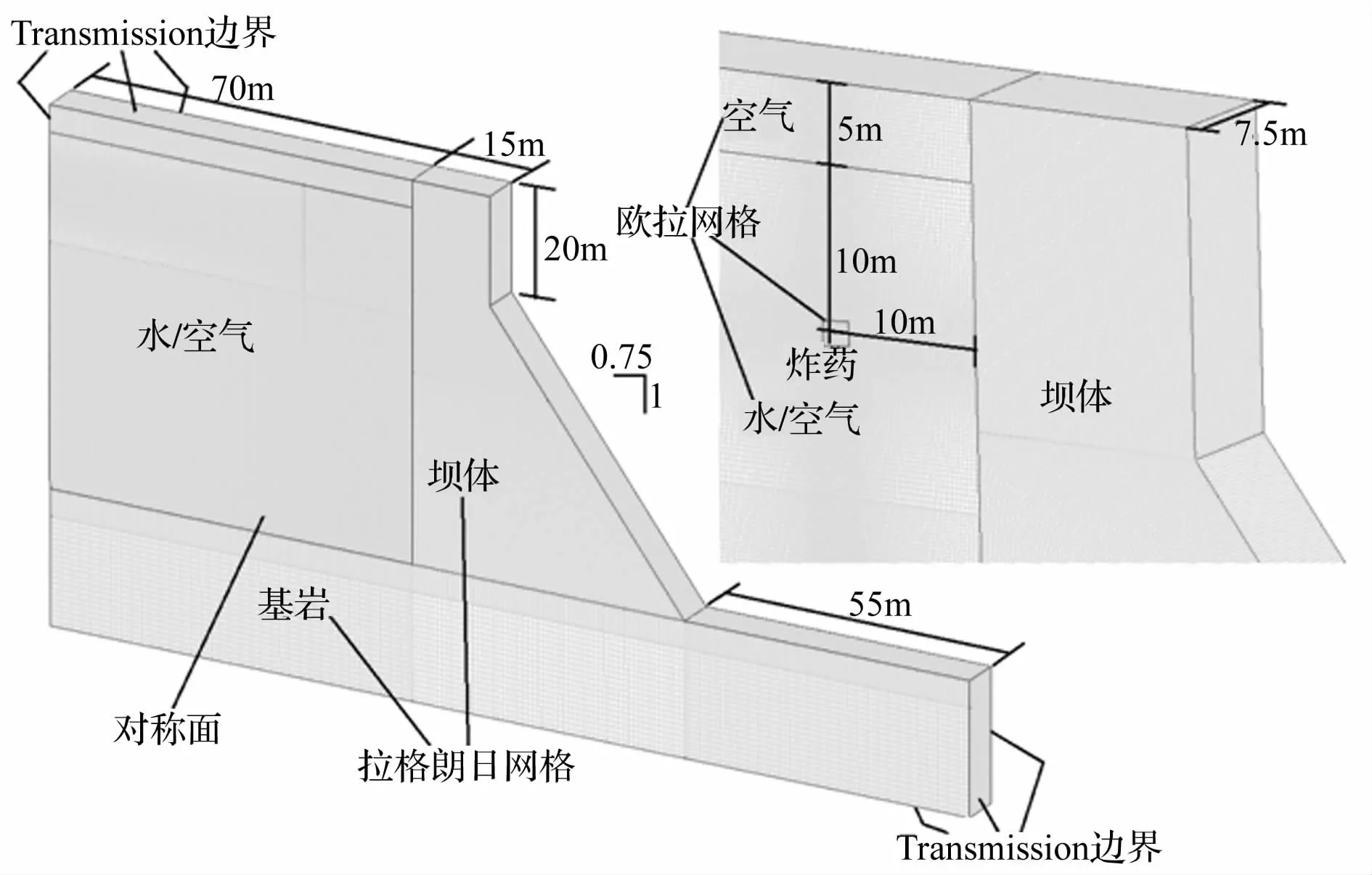
图6 水下／空中爆炸计算模型Fig．6 The calculate model of underwater explosion and air blast

图7 坝体上的测点布置图Fig．7 Arrangement of target points in dam

边界条件：基岩底部施加全约束，并在边界上定义无反射边界条件，使得人工边界上无冲击波反射，用这种方法来模拟半无限区域；除在库水、空气与坝体交接处外，库水和空气其它面均定义为无反射边界条件，以此来模拟库水和空气的无限区域。

4．2 不同爆炸方式下混凝土重力坝的动态响应

图8和图9分别给出了水下爆炸和空中爆炸时的压力云图。由图8和图9对比可得，同等药量炸药在水下爆炸产生的冲击波强度大于在空中爆炸产生的冲击波；在空气中传播的冲击波能量耗散的速度要比在水下传播的冲击波快；冲击波在自由水面会产生水面切断效应，能量传播受到阻碍，但在水－坝体和空气－坝体的交界面传播时较为顺利。由图8（b）可得，近自由面水下爆炸时，冲击波在自由面反射的稀疏波强度较大，与入射冲击波相互作用后使得自由水面下方的水压力迅速降低，产生局部空化效应，对靠近自由水面的坝体造成一定损伤。

图8 水下爆炸时的坝体压力云图Fig．8 Pressure contour from the dam subjected to explosions in water

图9 空中爆炸时的坝体压力云图Fig．9 Pressure contour from the dam subjected to explosions in air

图10 给出了水下和空中爆炸时大坝上游面和下游面计算点（计算点1＃和2＃）的压力时程曲线对比。由图10可得，冲击波传播到下游面时，反射形成强拉伸波；在下游面，峰值反射压力远远大于入射冲击波压力；药量相同时，水下爆炸冲击波的强度要大于空中爆炸冲击波。由图10（a）可得，空中爆炸时坝体内冲击波的最大峰值压力为1．52 MPa，水下爆炸时该值为34．86 MPa（几乎是空中爆炸的30．02倍）。由图10（b）可得，空中爆炸时大坝下游面反射波的最大峰值压力为0．45 MPa，水下爆炸时该值为5．52 MPa（几乎是空中爆炸的12．22倍）。

图11给出了水下和空中爆炸时坝顶计算点（计算点3＃）的速度时程曲线及加速度时程曲线对比。由图11（a）可得，水下爆炸时，坝顶的最大速度约为1．79 m／s；空中爆炸时，坝顶的最大速度约为 0．45 m／s；由图11（b）可得，水下爆炸时坝顶的加速度的震荡幅度明显大于空中爆炸时。综上所述，水下爆炸时大坝的动态响应比空中爆炸时剧烈。

图12给出了水下爆炸冲击荷载作用下坝体损伤破坏过程（云图中0～1代表坝体从未损伤到完全破坏）。由图12可得，爆炸冲击波对坝体中上部造成了严重的局部损伤破坏。损伤破坏开始主要出现在坝体上游面正对起爆点处、自由面与坝体交接处以及大坝下游面处。坝体上游面正对起爆点处直接受到爆炸冲击波冲击作用而使得混凝土出现压碎破坏；在自由面与坝体交接处由区域空化效应导致开裂损伤，且该损伤破坏不断向坝体内部扩展，可形成贯穿上下游面的贯穿性裂缝；当冲击波传播至大坝下游面时，将反射形成强拉伸波，由于混凝土的低抗拉强度特性，将在坝体下游面处产生损伤拉伸破坏。由于坝体的整体响应，坝踵也将产生拉伸损伤破坏。

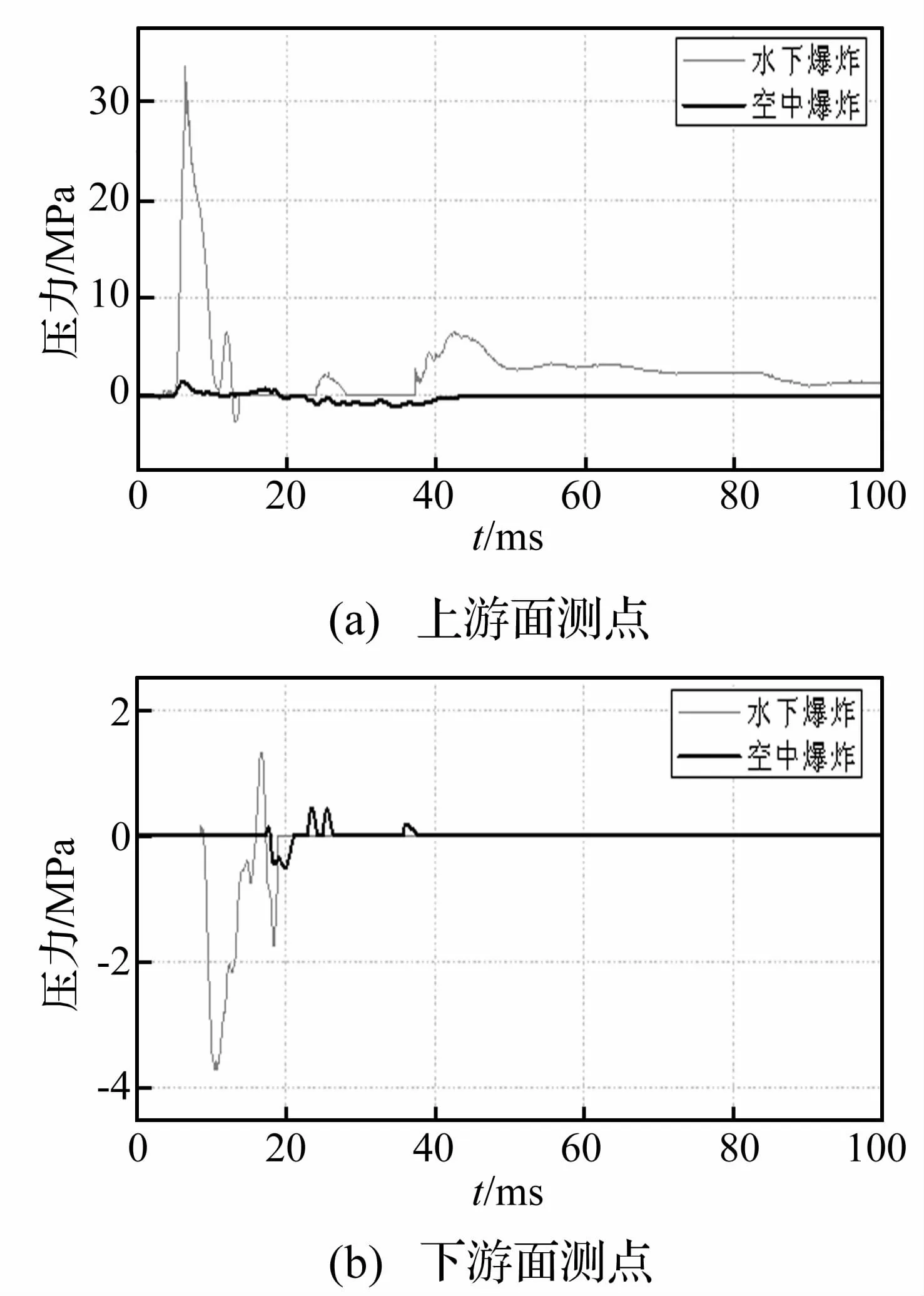
图10 水下和空中爆炸时坝体计算点的压力时程曲线的对比Fig．10 Comparison of stress wave in the dam subjected to explosions in water and air

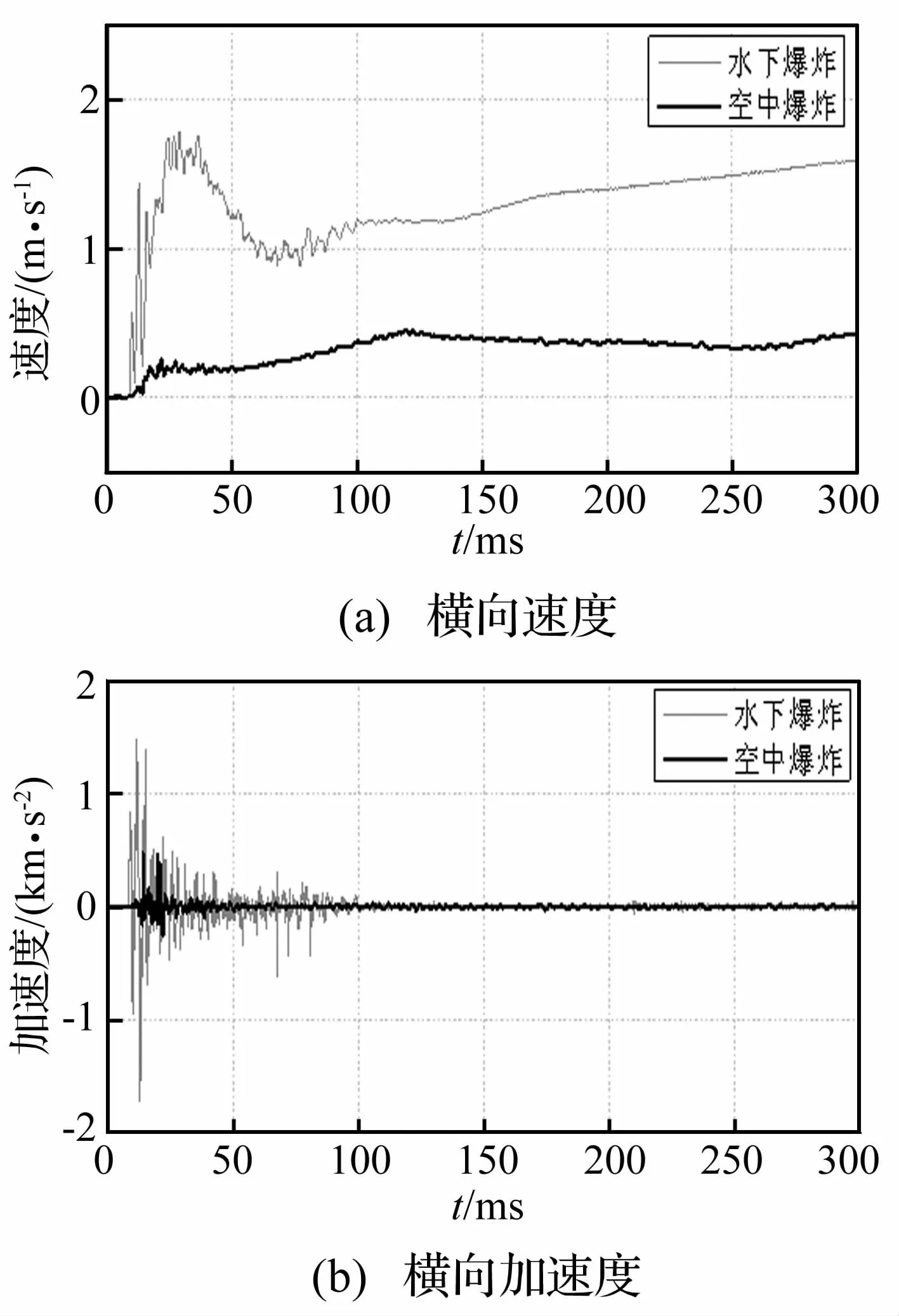
图11 水下和空中爆炸时坝顶测点横向速度及加速度对比Fig．11 Comparison of horizontal velocity and acceleration time histories

图12 水下爆炸时大坝的损伤过程Fig．12 The accumulated damage propagation process of the dam subjected to underwater explosion

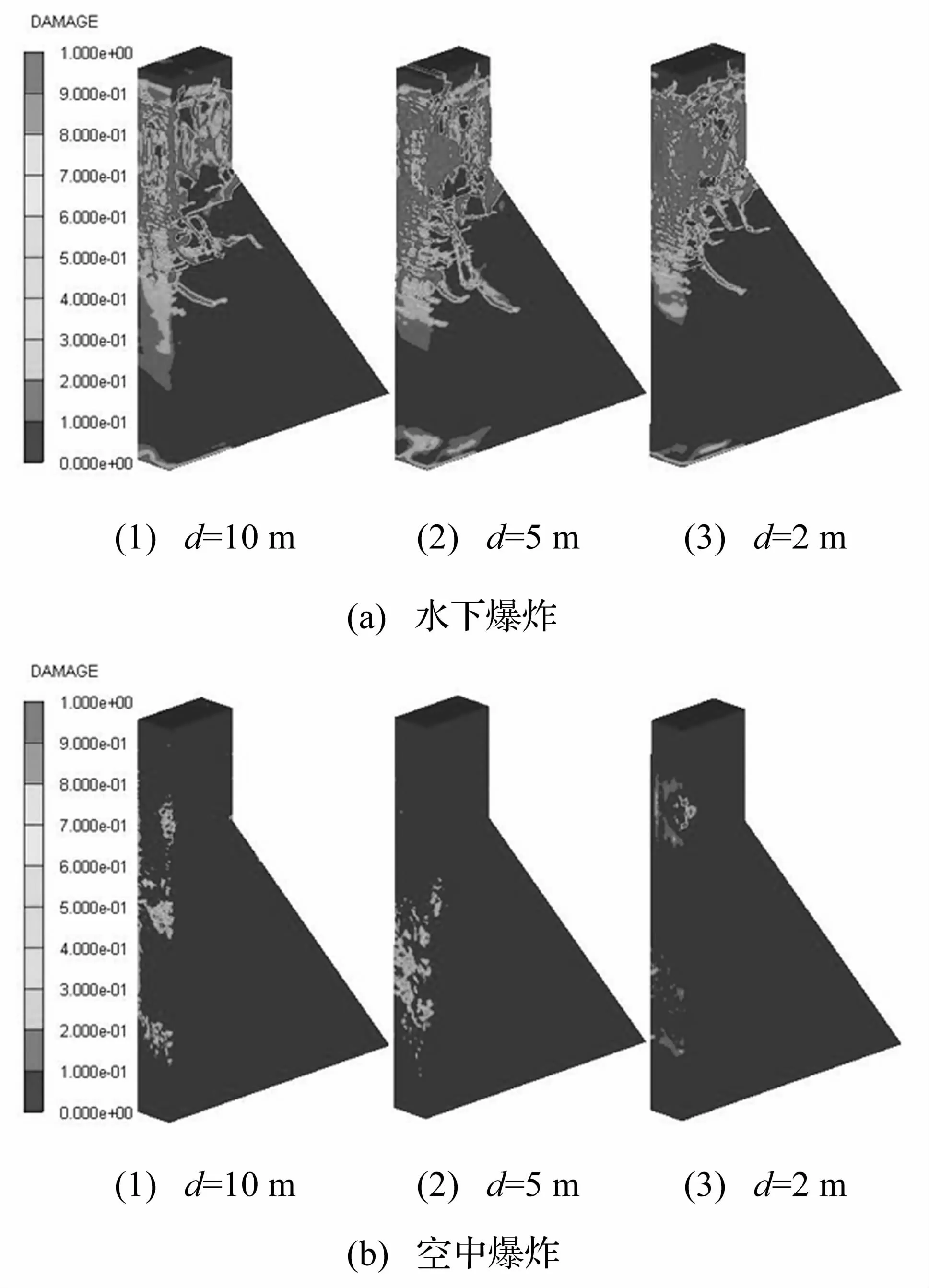
图13 水下和空中爆炸时大坝的损伤程度对比Fig．13 Comparison of damage level of concrete gravity dams from explosion in water and air

图13 给出了不同爆心距（记为“d”）时水下爆炸和空中爆炸荷载作用下的混凝土重力坝损伤情况对比。由图13可得，不同爆心距下，坝体在空中爆炸冲击荷载作用下的损伤破坏程度明显小于相同炸药量的水下爆炸，只在上游面出现较小范围的局部损伤，可见，水下爆炸产生的冲击波对大坝的破坏作用强于空中爆炸，更易造成大坝结构的破坏。因此，要特别注意混凝土重力坝在水下爆炸冲击荷载作用下的动态响应和损伤过程。由图13（a）可得，由于水下爆炸荷载的直接作用及其推动产生的水压力作用下，随着爆心距的减小，大坝的坝头部分损伤得愈发严重；由图13（b）可得，由于空中爆炸的能量在传播的过程中被大量耗散，随着爆心距的减小，大坝损伤加剧的程度不明显。

5 结 论

本文通过建立自由场及混凝土重力坝水下和空中爆炸的耦合数值模型，对自由场水下和空中爆炸冲击波的传播特性进行了对比分析，并进一步对比研究了大坝在水下和空中爆炸冲击波荷载作用下的动态响应。主要结论如下：

（1）爆炸冲击波在水和空气中的传播特性存在较大差异。相较于空中爆炸冲击波，水下爆炸冲击波具有压力峰值高（平均为空中爆炸下的42．35倍）、冲量大（平均为空中爆炸下的72．00倍）的特点。

（2）在装药量、起爆位置及爆心距均相同时，水下爆炸冲击荷载作用下混凝土重力坝动态响应及损伤程度较同等炸药量下空中爆炸冲击荷载作用时大。水下爆炸冲击作用下，坝体损伤首先出现在坝体上游面正对起爆点处，自由面与坝体交接处以及大坝下游面处，随着冲击波的传播裂缝向坝体内部扩展并形成贯穿性裂缝；空中爆炸冲击下，坝体损伤破坏主要出现在大坝上游面，损伤范围及程度较小，对大坝整体抗爆性能影响较小。在研究水工大坝抗爆性能时，应重点关注水下爆炸下大坝的动态响应及损伤特性。

［1］Rajendran R，Lee J M．Blast loaded plates［J］．Marine Structures，2009，22（2）：99－127．

［2］宁心，李晓炎，杨志焕．水下冲击波和空气冲击波传播速度及物理参数的对比研究［J］．解放军医学杂志，2004，29（2）：97－99．NING Xin， LI Xiao-yan，YANG Zhi-huan et al． A comparative study on the propagation speed and physical parameters of underwater blast wave and air blast wave［J］．Med J Chin PLA，2004，29（2）：97－99．

［3］Kwak H Y，Kang K M，Ko I，et al．Fire-ball expansion and subsequent shock wave propagation from explosives detonation［J］．International Journal of Thermal Sciences，2012，59：9－16．

［4］Clutter JK，Stahl M．Hydrocode simulations of air and water shocks for facility vulnerability assessments［J］．Journal of Hazardous Materials，2004，106（1）：9－24．

［5］Librescu L， Oh S Y， Hohe J． Dynamic response of anisotropic sandwich flat panels to underwater and in-air explosions［J］． International Journal of Solids and Structures，2006，43（13）：3794－3816．

［6］黄建松，汪玉．水下和空中爆炸舰员冲击损伤效应分析［J］．噪声与振动控制，2012，32（6）：13－16．HUANG Jian-song，WANG Yu．Analysis of shock injury of ship personnel due to underwater and air explosion［J］．Noise and Vibration Control，2012，32（6）：13－16．

［7］张社荣，王高辉，王超，等．水下爆炸冲击荷载作用下混凝土重力坝的破坏模式［J］．爆炸与冲击，2012，32（5）：501－507．ZHANG She-rong，WANG Gao-hui，WANG Chao，et al．Failure mode analysis of concrete gravity dam subjected to underwater explosion［J］．Explosion and Shock Waves，2012，32（5）：501－507．

［8］张社荣，王高辉．混凝土重力坝抗爆性能及抗爆措施研究［J］．水利学报，2012，43（10）：1202－1213．ZHANG She-rong，WANG Gao-hui．Study on the antiknock performance and measures of concrete gravity dam［J］．Shuili Xuebao，2012，43（10）：1202－1213．

［9］Riedel W，Thoma K，Hiermaier S，et al．Penetration of reinforced concrete by BETA－B－500 numerical analysis using a new macroscopic concrete model for hydrocodes［C］／／Proceedings of the 9th International Symposium on the Effects of Munitions with Structures，1999．

［10］Riedel W． Beton unter dynamischen Lasten： Meso-und makromechanische Modelle und ihre Parameter［M］．Fraunhofer-IRB-Verlag，2000．

［11］ Johnson G R，Holmquist T J．Response of boron carbide subjected to large strains， high strain rates， and high pressures［J］．Journal of Applied Physics，1999，85（12）：8060－8073．

［12］ANSYSInc．AUTODYN user manual version 13；2010．

［13］Benson D J． Computational methods in Lagrangian and Eulerian hydrocodes［J］．Computer Methods in Applied Mechanics and Engineering，1992，99（2）：235－394．

［14］Van der Veen W A．Simulation of a compartmented airbag deployment using an explicit， coupled Euler／Lagranginan method with adaptive Euler domains ［C］． In：NAFEMS，2003．

［15］张雄，陆明万，王建军．任意拉格朗日－欧拉描述法研究进展［J］．计算力学学报，1997，14（1）：92－101．ZHANG Xiong，LU Ming-wan，WANG Jian-jun．Research progress in arbitrary Lagrangian-Eulerian method ［J］．Chinese Journal of Computational Mechanics，1997，14（1）：92－101．

［16］Cole R H，Weller R．Underwater explosions［J］．Physics Today，1948，1：35．

［17］Kinney G F，Graham K J．Explosive shocks in air［J］．Berlin and New York， Springer-Verlag，1985，282 p．，1985，1．