关于瓷套变形问题的探讨

焦国锋,李风芹,范建二,顾瑞云

(1.南京电气集团有限责任公司,江苏南京210038;2.南京工业职业技术学院,江苏南京210046)

0 引言

图1 电容瓷套

大瓷套的变形是瓷套生产过程中一个常见的产品缺陷。变形有多种形式,如瓷套的孔口椭圆变形、瓷套的轴向弯曲变形等,本文主要针对瓷套轴向弯曲变形进行讨论。

瓷套的弯曲变形与料方的性能以及工艺过程控制等都有密切的关系,但在生产中曾经发现这样一个现象:电容瓷套(b)和电容瓷套(a)在几何尺寸方面是非常相近的两个产品(图1),但是从数次检测的结果看,003621－9.2产品变形相对较多、较大。比较两个产品发现,两个产品的伞伸出、下内孔以及壁厚均接近,较大的区别是003621－6.2图1(a)直体部分比003621－9.2短,重心低47 mm,质量少21 kg。长期的生产经验认为,当产品的质量越重(质量越大),产品高度高,重心高,产品变形倾向越大。因此选择瓷套的质量(m)、瓷套重心距离瓷套下端面高度h与自身总高度H的比(h/H)以及瓷套的稳度(W)对瓷套变形情况加以统计分析。

1 对统计量的说明以及进一步选择

2.1 稳度(W)

稳度是把物体翻倒的难易程度,物体稳度大小一般用翻倒它时所做功来描述。图2所示AO是瓷套重心O所在铅垂线,AB是瓷套底面半径,BC∥AO,且BC＝AO。当瓷套重心O沿圆弧OD移动到D后,则瓷套自动倾倒。在这个过程中O升高距离CD,所做的功可用下式表示:

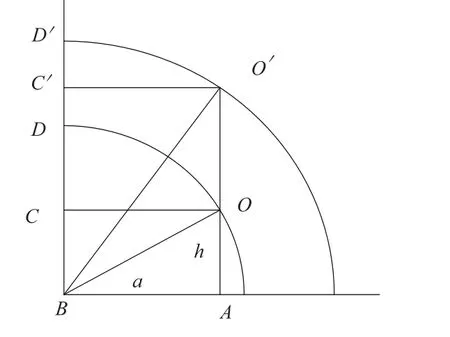
图2 稳度示意图

知稳度是a的增函数,a变大时W变大。

物体G不变,当重心O提高到O′,由图2可明显看出即重心提高使物体稳度降低。

1.2 关于瓷套重心Z和重心高度h

因为所研究的瓷套体积不太大,可认为瓷套处于均匀的重力场中(即瓷套体积内各处的重力加速度g大小相等,方向平行),瓷套重心与质心的位置是重合的。通过CAD绘图可求得瓷套质心,即瓷套重心,同时也可求得重心距瓷套底面的高度h,从而可以进一步计算h与H(瓷套自身高度)的比。

1.3 瓷套的质量(m)与(h/H)以及统计量的选择

经验认为,瓷套质量m越大,瓷套所受的重力越大,由于瓷套高温荷重能力的限制,因此更容易产生变形。

从稳度的计算式(1)看,物体质量m与稳度W是相关的,因为公式中G＝mg。为了选择相对独立的统计量,根据相关系数计算公式:

式中:xi,yi——所选统计量的观测值;

利用表1中的数据,计算所选统计量间的相关系数如表2。

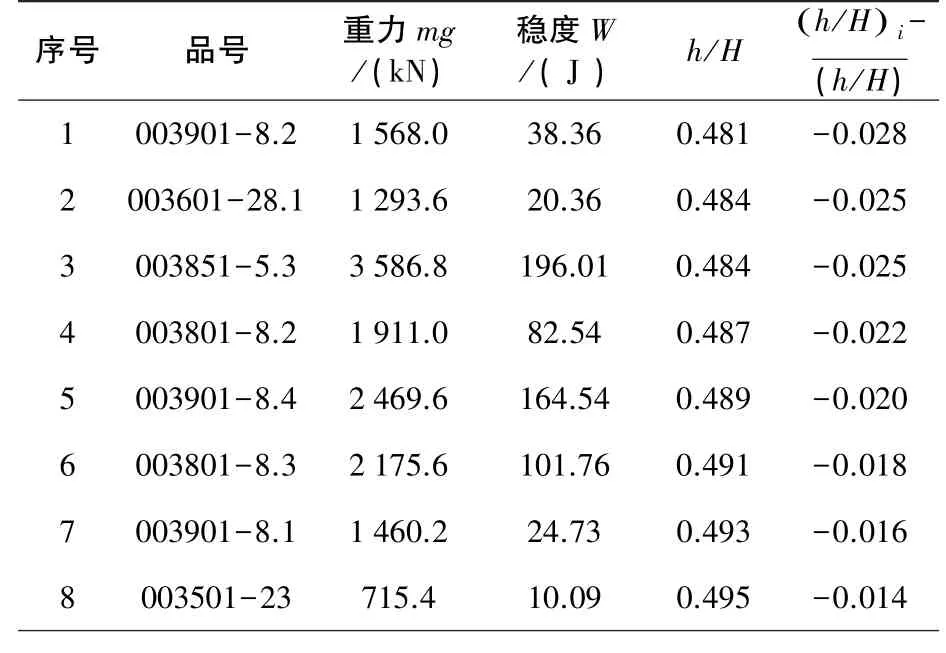
表1 相对变形较大、易产生变形的瓷套类

续表1

表2 各统计量间的相关性

通过表2中数据可看出,瓷套质量m与瓷套稳度W有较强的相关性(相关系数是0.912)。因此可取其一作为统计量,另外瓷套质量m与h/H(瓷套重心距离瓷套下端面高度与瓷套总高度之比)的相关系数是0.167,瓷套稳度W与h/H的相关系数是0.013,因此选择W与h/H作为统计量。

2 抽样分析

2.1 排序分析

抽取样本如表3所示。针对统计量(W与h/H)分别排序分析,按稳度W列排序,未发现规律;但是h/H列按升序排列后,规律性较强,与生产实际相对照:17行之前各产品相对变形小或不变形;17行之后各产品相对变形较大或易产生变形。因此将表3中数据分为两类列于表1和表4中。

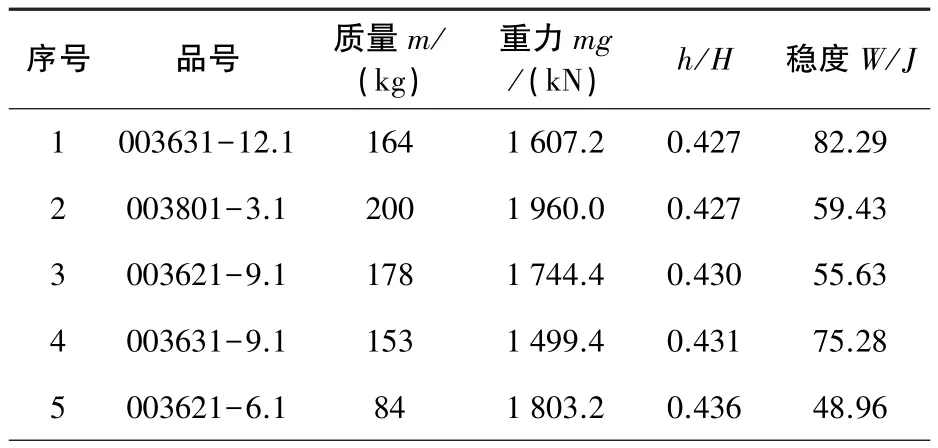
表3 样本按重心高度h与瓷套高度H之比(h/H)排序

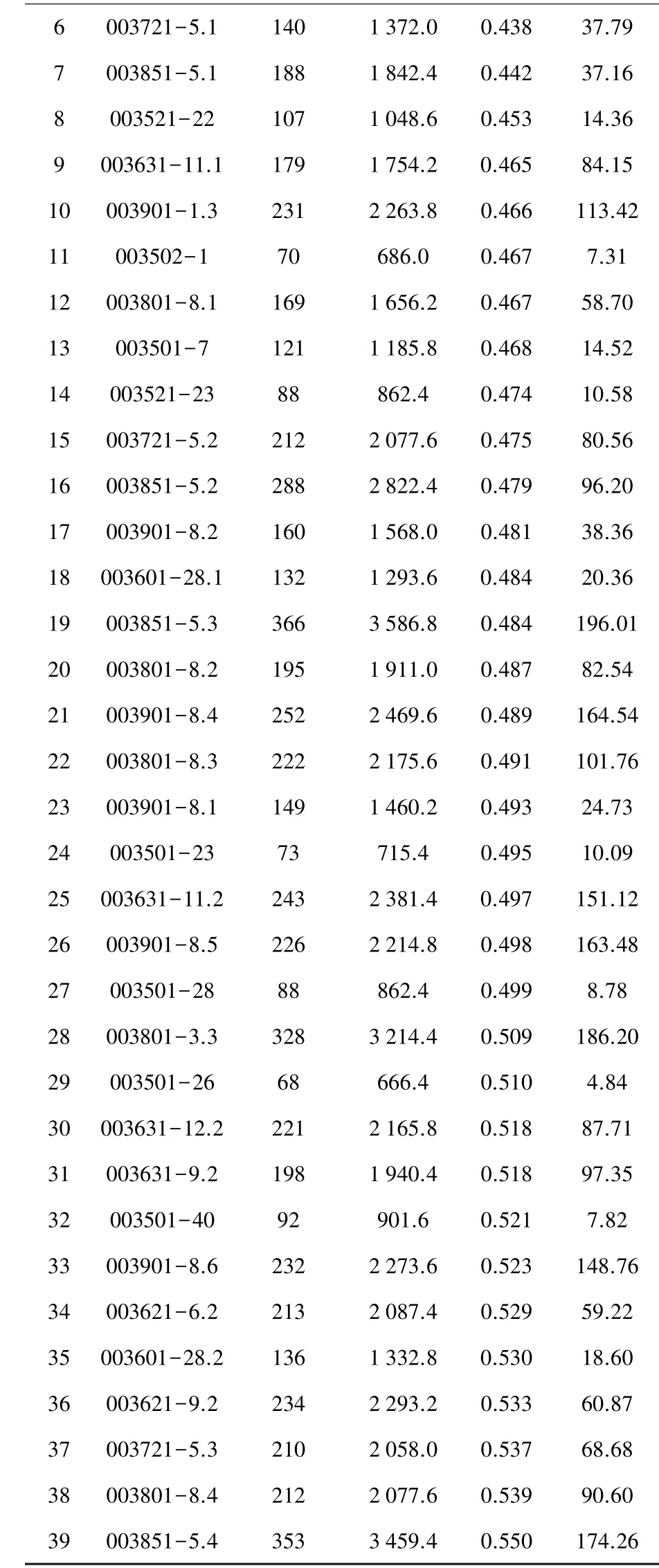
续表3

表4 相对变形小或不变形的瓷套类

续表4_

通过排序发现用稳度W大小来描述产品变形情况,与生产实际的符合性不好,因为有些产品的稳度值很小,很接近,但却是两种相反的情况。

如表5所示003501－23和003521－23的稳度值很接近,而003502－1产品的稳度值甚至小于003501－23,但是003521－23、003502－1由于是带锥度的塔形产品,所以变形很少(表5中所列带锥度的塔形产品均变形很少),而003501－23由于是直筒形的产品,所以变形较多。因此产品的几何形状对产品的变形有较大影响。

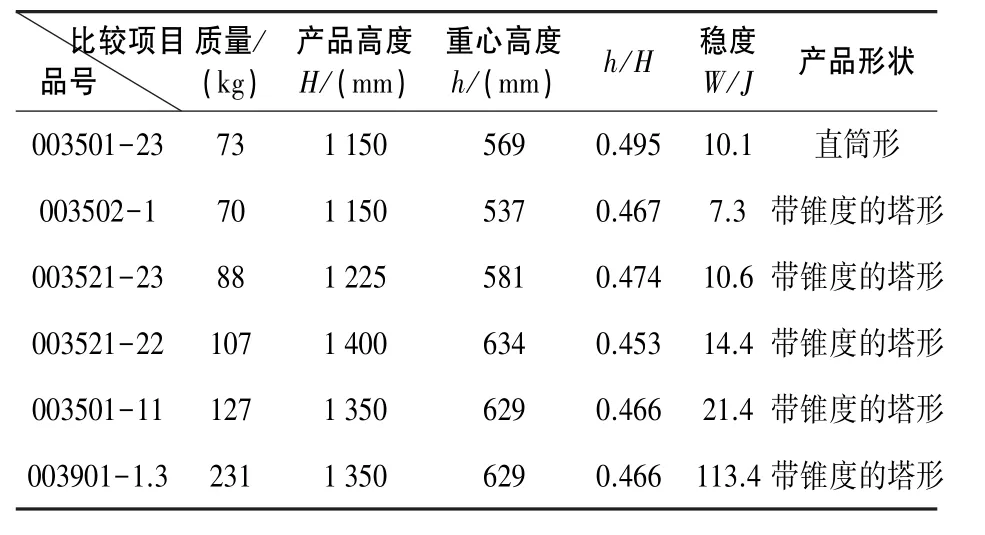
表5 稳度W与h/H统计量的比较

稳度的计算关系到了产品的几何形状,但是用瓷套重心高度与产品自身高度的比来描述瓷套的稳度更确切,因为重心是由瓷套的几何形状和瓷的质量分布均匀性确定的,瓷的质量分布可以认为是均一的(即瓷的体积密度是均一的),所以瓷套的重心与瓷套的几何形状密切相关,另外瓷套均近似为圆筒形,可抽象为“直杆”,一根头重脚轻的杆更容易倾倒,是一个简单的物理现象,而h/H描述了“杆”“头重”的程度,因此用h/H描述瓷套的稳度更确切,以下分析主要针对h/H统计量进行分析。

由表5还可以看出,瓷套的质量和自身高度对瓷套的变形不是决定性的。如003501－11和003521－22两个产品的自身高度和质量都大于003501－23产品的高度和质量,而它们的变形很少(表中003901－1.3产品的情况更能说明该问题)。因此经验认为瓷套的质量大、高度高,就产生变形,是一种不准确的认识。

2.2 对两类产品总体参数推断分析

1)相对变形小或不变形类瓷套(h/H)总体均值的区间估计

选择显著性水平a＝0.05,计算(h/H)总体均值95%的置信区间。a/2＝0.025,由表2知 n＝16。

因为总体方差σ2未知,因此选择随机变量

通过以上计算知:相对变形小或不变形类产品(h/H)总体均值u的95%置信区间是[0.443,0.463]。

2)相对变形较大、易产生变形的瓷套类(h/H)总体均值的区间估计

选择显著性水平a＝0.05,根据表1数据对该类瓷套(h/H)总体均值进行区间估计,计算步骤同1),计算结果如表6。

表6 相对变形较大、易产生变形的瓷套类(h/H)总体均值的区间估计

3 结语

1)经验认为瓷套的质量大、高度高,会产生变形,是一种不准确的认识。

2)瓷套的几何形状对变形有较大的影响,采用统计量h/H能较好地判别瓷套的变形。通过对相对变形小或不变形类瓷套(h/H)总体均值的区间估计,和相对变形较大、易产生变形的瓷套类(h/H)总体均值的区间估计,认为只要瓷套的(h/H)接近或超过0.500,即会产生弯曲变形的倾向。

3)对于公司现在使用的产品配方和现有的产品,通过以上计算知:相对变形小或不变形类瓷套(h/H)总体均值u的95%置信区间是[0.443,0.463];相对变形较大或易产生变形类瓷套(h/H)总体均值u的95%置信区间是[0.500,0.518]。

[1]全国质量专业技术人员职业资格考试办公室组织编写.质量专业理论与实务[M].北京:中国人事出版社,2007.1.

[2]何灿芝,吴俊杰.概率论与数理统计[M].湖南:科学技术出版社,1994.

[3]王式安.数理统计方法及应用模型[M].北京:北京科学技术出版社,1992.11.

[4]李济群.AUTO CAD机械制图基础教程[M].北京:清华大学出版社,2011.5.