布朗运动仿真实验的设计与实现

丁望峰

（杭州师范大学理学院，浙江杭州 310036）

布朗运动仿真实验的设计与实现

丁望峰

（杭州师范大学理学院，浙江杭州 310036）

介绍了布朗运动仿真实验的设计与实现方法，利用“位置朗之万方程”的数值离散化，最大程度还原真实的布朗运动.通过对仿真实验数据的定量分析，并计算出了阿伏加德罗常量的近似值.

布朗运动；仿真实验；阿伏加德罗常量

1 引 言

1827年，英国植物学家罗伯特·布朗（Robert Brown）在显微镜下观察悬浮在水中的花粉时，发现花粉粒子会不停地进行连续不规则的运动.次年他以《植物花粉的显微观察》为题发表论文来描述这种运动，后来就以他的名字来命名这一现象［1］.由于当时人们的认识还没有达到分子层面，一时产生了不少观点.直到1905年前后爱因斯坦（Albert Einstein）发表了他有关布朗运动的论文，才第一次对这种不规则运动进行定量地分析.在他文章的最后，爱因斯坦还给出了验证理论正确性的方法［2］：

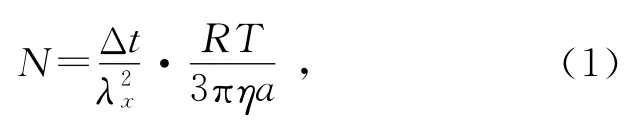
这里对原文中的部分符号作了修改，其中N是阿伏加德罗常量，Δt是运动轨迹上邻近2个记录点的时间间隔，R是气体常量，T是实验温度，η是实验温度下液体的黏度，a是球形微粒的半径.在实验上，每隔时间Δt记录1次布朗颗粒的坐标，可以得到布朗运动的轨迹图.通过测量颗粒在x方向上位移的平均平方值λ2x，就可以根据式（1）计算出阿伏加德罗常量的实验测量值.

布朗运动实验是对分子理论正确性很好的验证，通过上面简单的式子，就可以从布朗运动轨迹计算出阿伏加德罗常量的估算值，是一个很好的大学物理实验项目.但目前相关教学实验大都停留在定性的演示层面，要进行定量测量却存在诸多困难［3，4］.首先，传统的显微镜虽然能很好地观测布朗运动，但却无法精确记录其运动轨迹，同时还存在尺度标定等问题.虽然一些实验室已配备带图像采集系统的数字显微镜，但其价格不菲，不适合开展大规模教学.其次，由于不能确定哪些颗粒会进入视野，而对运动的颗粒进行尺寸测量非常困难，所以实验所用的微粒小球尺寸需要精确订制.另外，观测区内一般会有多颗微粒，要想对1个颗粒进行追踪，实验操作上也有很大的难度.

为了解决以上难题，笔者设计了布朗运动的仿真实验，能保证最大程度地还原真实的实验条件和现象，加深学生对布朗运动的理解.整个仿真实验采用Java语言开发，同时提供Java应用程序和Java Applet两种版本，后者可以嵌入网页供学生远程操作.

2 实验原理

布朗运动的模拟通过求解朗之万方程（Langevin equation）来实现［5，6］：

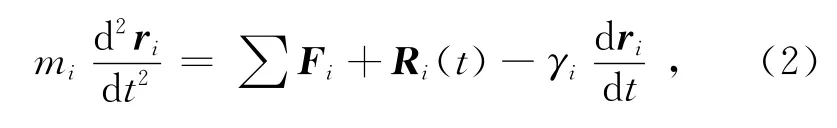
其中η是液体黏度.

根据随机耗散理论，随机作用项Ri（t）与摩擦系数满足如下关系

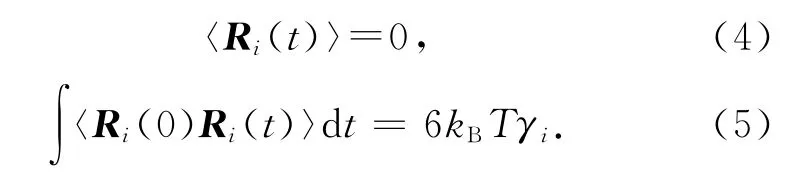
在实际模拟中，往往假定随机作用力在不同时刻是不相关的，即式（5）可采用如下形式

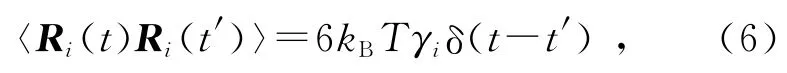
式（6）把布朗粒子受到的随机热扰动与体系温度及摩擦系数关联起来.

当液体的黏滞阻力相对于布朗粒子而言很大时，布朗粒子看上去像没有惯性质量一样地运动，这时式（2）等号右边可近似为零，即

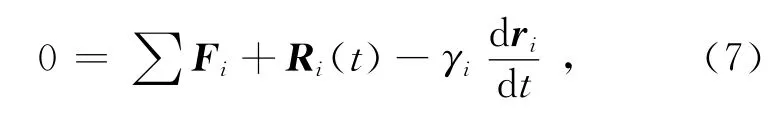
该等式也被称为“位置朗之万方程”，是朗之万方程的“过阻尼”形式［6］.利用式（7）进行的动力学模拟称为布朗动力学（Brownian dynamics）.

仿真实验是基于式（7）的数值离散化来完成的.计算机数值化模拟把连续的真实的物理过程分割成时间间隔为Δt的状态点，通过计算从t时刻到t＋Δt时刻状态点的演化来实现模拟.这里记位矢ri的三维坐标为（x1，x2，x3），则再根据式（7），xα（α＝1，2，3）方向上粒子i从t到t＋Δt的演化方程为

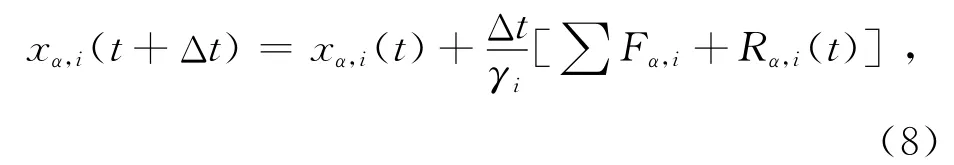
从上式可以看出，位置朗之万方程中并不出现速度，粒子下一步的走向完全取决于粒子此刻受到的明确作用力和热扰动产生的随机作用力.由于本文中的布朗运动不考虑颗粒之间的相互作用，即∑Fα，i为零，上式可简化为

为了满足式（3）和式（4）要求，随机作用力Rα，i（t）可以取期望值为0、标准差为的高斯分布，记为

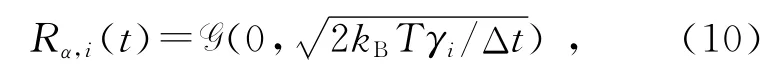
从式（9）和（10）可以看到，位置朗之万方程的具体实现已与颗粒的材质没有关系，而这正是布朗运动的特征之一.

3 实验设计

如图1所示，仿真实验界面分为实验观测区与实验参量控制区.左边的观测区是对布朗运动轨迹的显微放大，通过下面的倍率选择按钮可以选择不同的放大倍数.右边的参量控制区为实验提供了丰富的选项，实验者可以选取不同的实验参量，对布朗运动的诸多特性进行定性比较和定量分析，比如不同颗粒大小、密度，液体温度、黏度等对布朗运动的影响.如果只是观测实验现象，还可以设定较多的粒子数，不同的颗粒轨迹会用不同的颜色表示.当实验者设定好所有参量，就可以点击“开始”按钮开始实验，颗粒在观测区内的连续运动轨迹用曲线表示，设定时间间隔所记录的点用圆点表示.程序内部的模拟时钟与电脑时钟同步，如果选择每隔10 s记录1个点，那么记录30个点就需要300 s的时间.如果颗粒运动不明显或者越出了视野，可以实时地调节放大倍数，以达到最佳的观测效果.当记录了所需的足够点后，选择停止并保存轨迹，所记录的点的坐标就会输出到文件.值得注意的是，保存的轨迹只是点的坐标，而并非实验过程中观测到的连续的曲线.

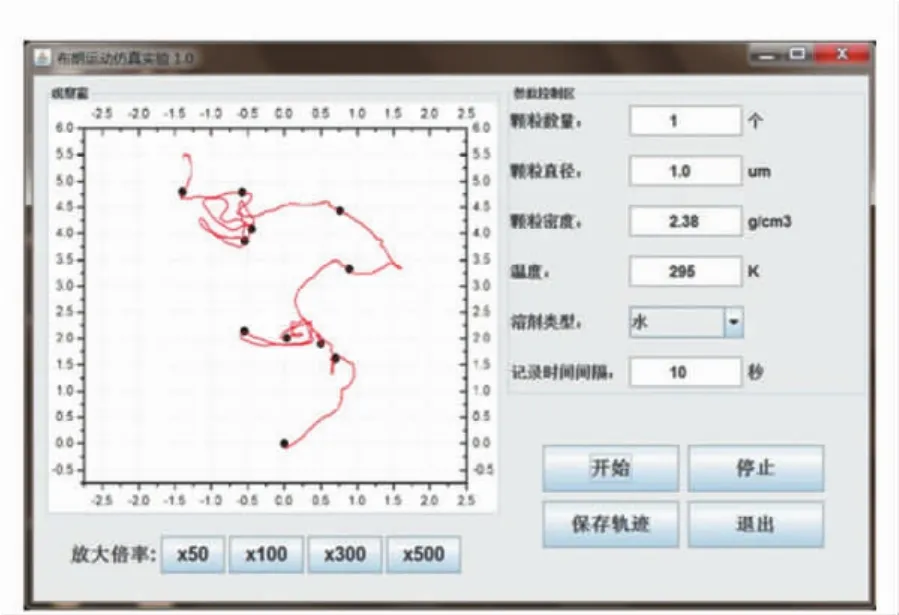
图1 布朗运动仿真实验界面

4 实验结果与分析

首先，做定性的分析.通过参量的调节，可以验证布朗运动的如下特性：

1）粒子运动永不停止，没有固定的轨迹；

2）运动随温度的升高而加剧；

3）运动速度与粒子大小成反正；

4）溶液的黏度减小时，布朗运动加剧；

5）粒子的成分或密度不会影响粒子的运动.

接下来，用爱因斯坦给出的式（1）进行定量分析.这里考虑直径1μm的SiO2颗粒在温度为295 K的水中的布朗运动，模拟的相关参量如下：直径为1.0μm，密度为2.38 g/cm3，温度为295.0 K，水的黏度为1.003 g/（m·s），时间步长为10 s。

图2中相邻两点的记录时间间隔为10 s，共记录了30个点.计算两点间的距离平方

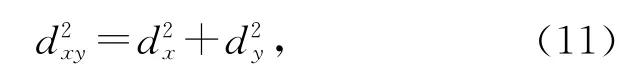
一共可得到29个数据，对其求平均

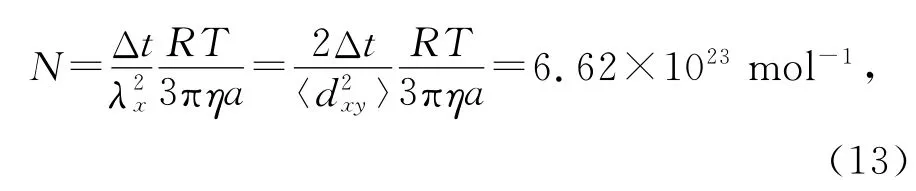
从计算结果来看，仅从少量的坐标数据就可以得到较为精确的阿伏加德罗常量值.

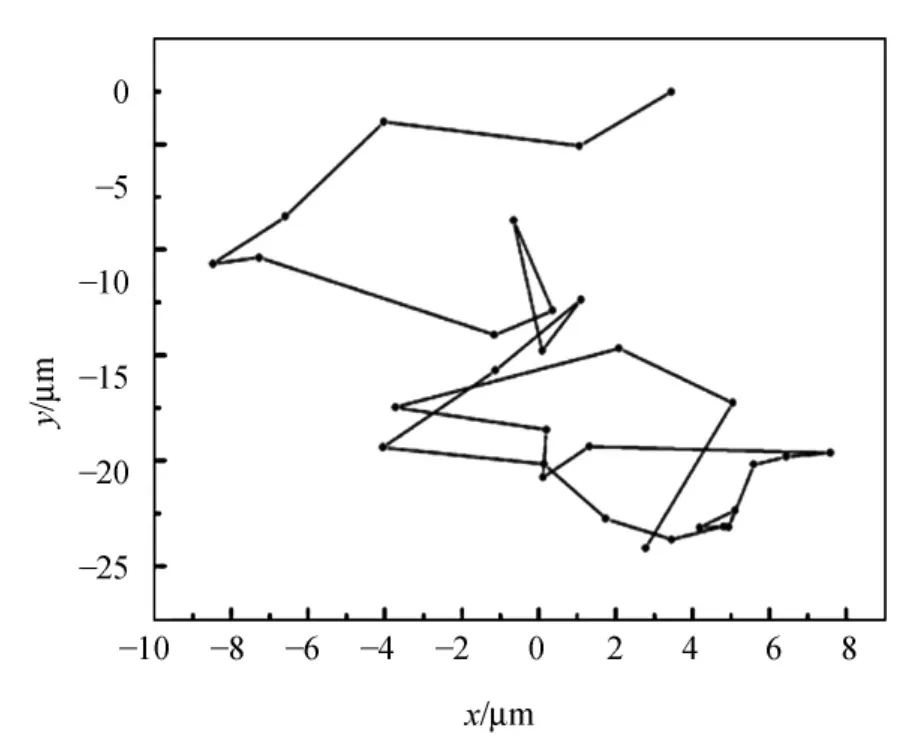
图2 直径为1μm的SiO2微粒在295 K的水中做布朗运动的轨迹

表1 对图2中的布朗运动轨迹的数值分析

5 结束语

本文介绍了布朗运动仿真实验原理，并据此设计开发出适合学生操作的仿真实验.模拟程序通过参量的调节，不仅能定性地展示布朗运动的特点，而且可以对布朗运动的轨迹进行定量分析，计算出较为精确的阿伏加德罗常量值，由此也验证了计算机仿真是对物理运动规律的真实反映.

［1］ 郝柏林.布朗运动理论一百年［J］.物理，2011，40（1）：1-7.

［2］ Einstein A.Investigations on the thoery of the Brownian movement［M］.New York：Dover，1956.

［3］ 李鸿寅.介绍布朗运动的一种演示实验 ［J］.物理实验，1981，1（1）：23-24.

［4］ 梁超联.用显微镜观察气体中的布朗运动［J］.物理实验，2000，20（8）：34.

［5］ 王子瑜，曹恒光.布朗运动、朗之万方程式、与布朗动力学［J］.物理，2005，27（3）：456-461.

［6］ Coffey W T，Kalmykov Yu P，Waldron J T.The Langevin Equation［M］.Second Edition.Singapore：World Scientific，2004.

［责任编辑：郭 伟］

Simulation experiment of Brownian motion

DING Wang-feng
（College of Science，Hangzhou Normal University，Hangzhou 310036，China）

The design and implement method of Brownian motion simulation experiment were introduced.The characteristics of real Brownian motion was maximally retained by the numerial discretization of position of Langevin equation.By quantitative analyzing of the motion traces，a close approximation of Avogadro constant was obtained.

Brownian motion；simulation experiment；Avogadro constant

O414.2；O4-39

A

1005-4642（2014）10-0038-03

2014-05-16；修改日期：2014-08-25

丁望峰（1984－），男，浙江义乌人，杭州师范大学理学院实验师，博士，主要从事实验物理方面教学工作.