功能梯度压电层／压磁半空间结构中SH波传播

孔艳平，田若萌，刘金喜

（石家庄铁道大学 工程力学系，石家庄 050043）

作为新型材料的功能梯度材料集各种组分于一体，其微观结构呈连续性变化可适应不同环境，实现某特殊功能［1－2］。压电材料可实现机械能与电能的转化，通过调整材料组成使梯度化可使压电系数获得最恰当分配以达到提高压电器件性能及寿命。对其研究多集中于对功能梯度梁、板、壳等基本结构的静态变形，对弹性波传播研究较有限。Qian等［3－5］用WKB方法研究功能梯度层状复合结构中Love波传播特性，分析材料梯度变化对频散特性影响。Eskandari等［6］用贝塞尔函数方法研究功能梯度压电材料中弹性波传播，材料中弹性、压电及介电系数为二次方变化，而材料密度为常数。Du等［7－8］研究均匀无限大磁电弹半空间覆盖有功能梯度磁电弹层结构中的SH波，考虑两种形式的电磁边界条件，分析梯度系数对相速度、群速度影响。Li等［9］研究横观各向同性磁电弹半空间中B－G波的传播性质，发现材料的非均匀性会致波频散。董小峰等［10］分析压电功能梯度材料中SH表面波，对材料特性沿厚度方向为线性、二次、三次函数变化的三种形式利用拉盖尔正交多项式法求得三种不同特性梯度材料中波的频散曲线、质点位移及电势。谢根全等［11］研究电磁功能梯度材料层合板中表面波的弥散特性，认为中间层材料性能沿厚度线性变化，数值算例显示压电性对频散性能影响较大，而压磁性影响可忽略。Wu等［12－13］用勒让德多项式方法分析磁电弹功能梯度板及空心圆柱中导波传播性能，认为板与空心柱体表面为机械自由、电学开路及磁学短路，导波传播速度与压电、压磁系数成正比，与介电常数、磁导率成反比。

本文研究功能梯度压电层／压磁结构中弹性波传播特性，从磁电弹全耦合方程出发，详细推导SH波传播的频散方程，分析材料性能、覆层厚度及电学边界条件对波的频散特性影响，结果可对压电压磁复合材料声波元件设计提供有价值的理论依据。

1 基本方程描述及求解

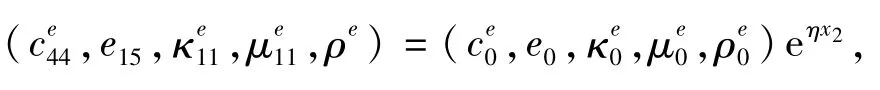
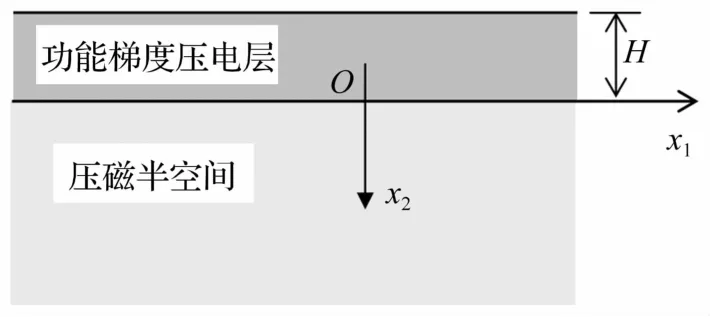
图1 问题的几何描述Fig.1 Geometry of the problem

压电层材料性能沿厚度方向指数变化，即弹性系数 c44、压电系数 e15、介电系数 κ11、磁导率 μ11、压磁系数h15、磁电弹耦合系数α11及压电层的密度ρ均为坐标x2的函数，考虑反平面磁电弹问题，其本构关系为

梯度方程为

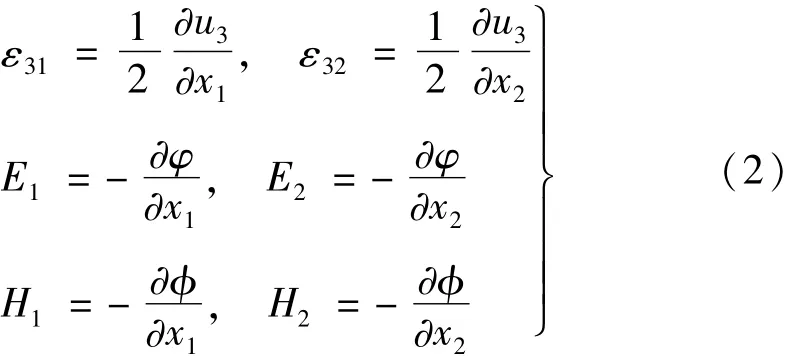
式中：u3为x3方向位移；φ为电势；为磁势。

运动方程为

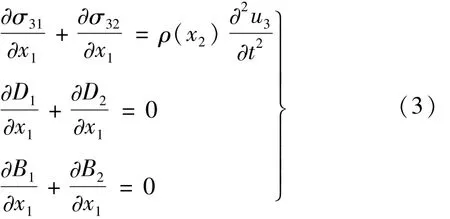
将式（1）、（2）代入方程（3）中得功能梯度磁电弹全耦合反平面问题的控制方程为

类似，令梯度系数η＝0，得均匀压磁材料的控制微分方程为

式中：e，m分别为压电层、压磁半空间的相应量。

2 问题的解

考虑结构中SH波解一般形式为

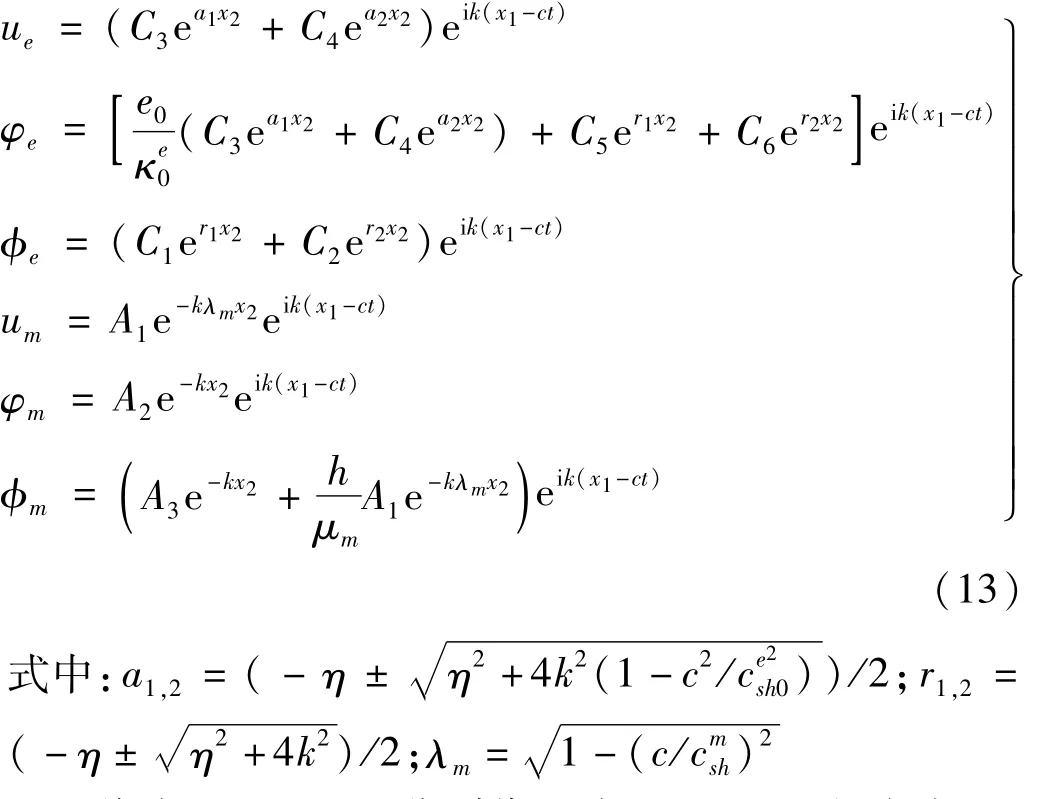
将式（12）、（13）分别代入式（6）、（8），得应力、电位移及磁感为

3 频散方程

设界面x2＝0处两种材料间理想粘结，界面条件为

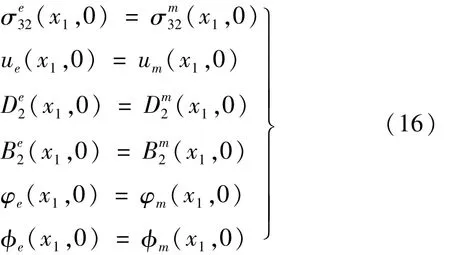
此处只讨论磁学开路情况，考虑电学短路、开路两种电边界条件，即

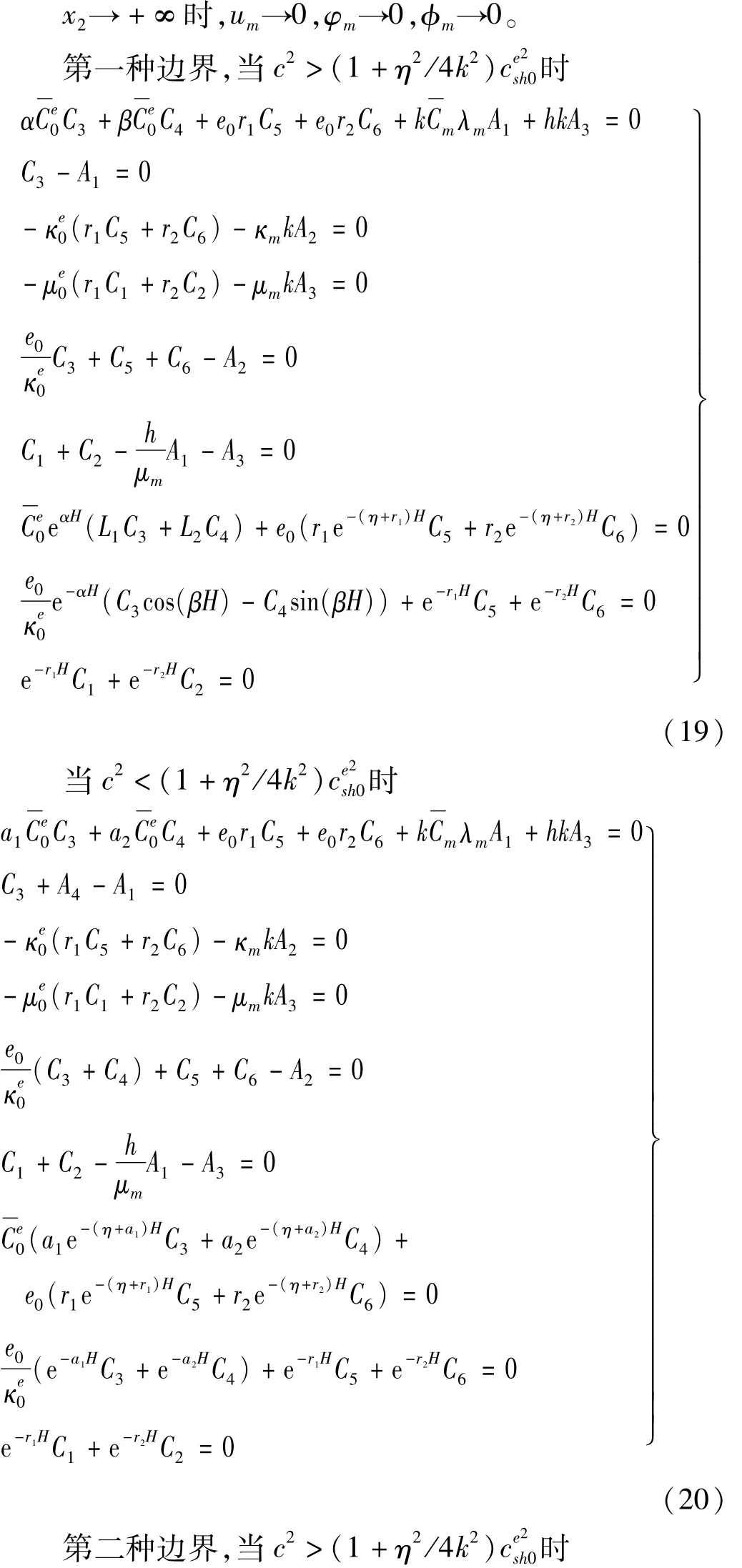
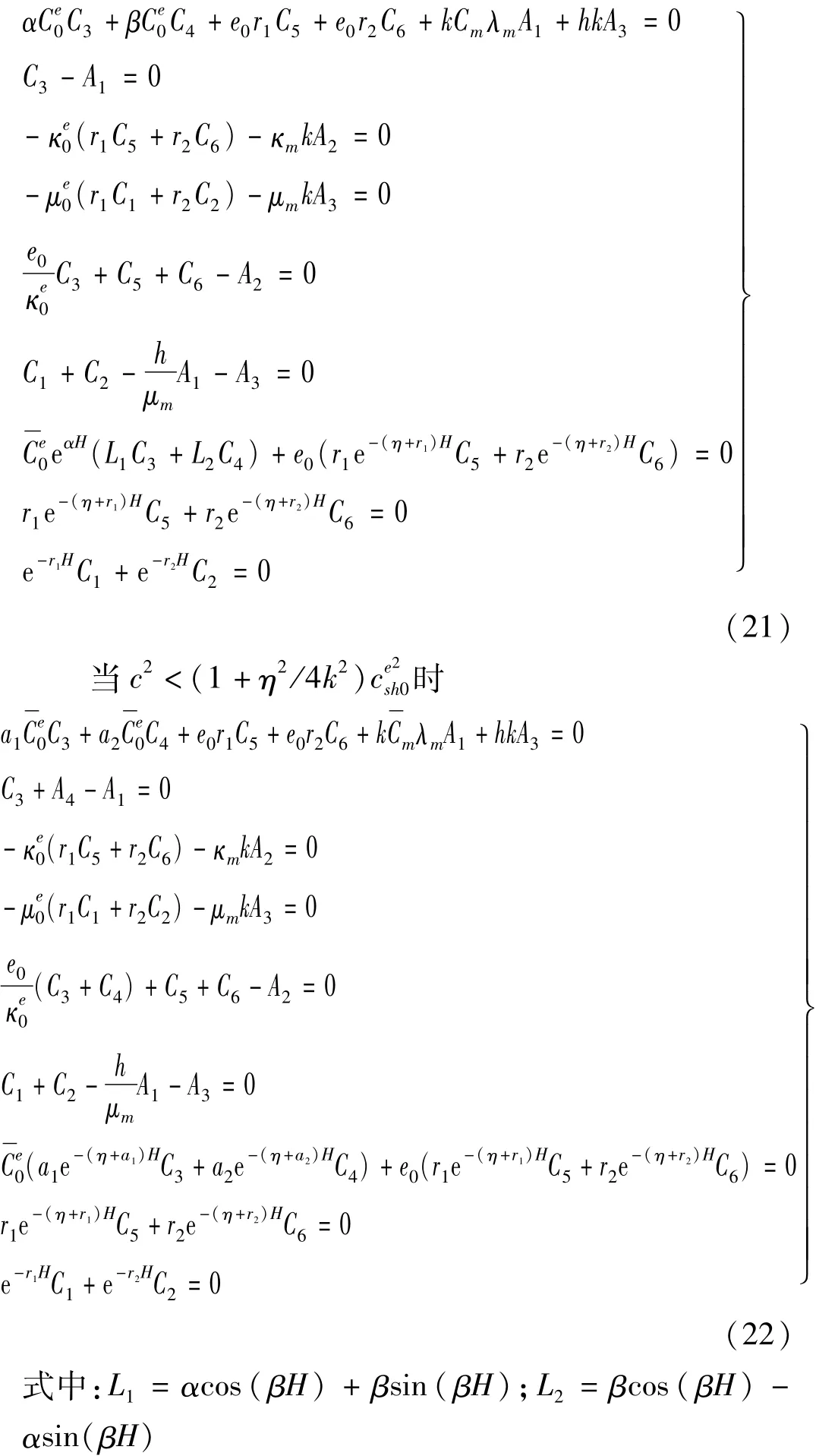
只有方程组（19）～（22）存在非零解，才能满足SH波在该结构中传播条件。故令方程组（19）～（22）系数矩阵行列式值为零，得第一种边界条件频散方程。

4 数值算例及分析

利用已推导的频散方程分析电学边界条件、功能梯度压电层中各材料参数梯度变化及覆层厚度对SH波频散特性影响。算例中横坐标K＝kH／2π为无量纲波数，纵坐标c／（m／s）为相速度。在x2＝0处压电材料取 PZT－5A，材料参数［14］为：ce0＝21.1×109C2·Nm－2，e0＝12.3 C·m－2，κe0＝8.107×10－9C2·Nm－1，μe0＝5×10－6NS2·C－2，ρe0＝7.75×103kg·m－3；压磁材料取 CoFe2O4，材料性能［15］为：cm＝45.3×109C2·Nm－2，h＝550 NA－1m－2，ρm＝5.3×103kg·m－3，μm＝1.57×10－8NS2·C－2。

4.1 电学短路边界条件下频散特性分析

为研究功能梯度压电层中各材料参数的梯度变化对SH波传播频散曲线影响，分别给出 PZT－5A／CoFe2O4结构在电学短路边界条件下梯度指数η取不同值时前四阶模态频散曲线见图2～图4。由图2看出，η＝0时功能梯度压电层变为均匀压电层，且曲线为均匀压电层／压磁半空间结构一阶频散曲线，与结论［16］吻合；梯度取小值、一阶模态在小波数时，随波数增大相速度急剧减小，且减小至功能梯度压电层界面处的B－G波波速；随梯度取值增大相速度的变化缓慢减小。原因为功能梯度压电材料梯度指数η越大，压电层剪切体波波速越小，故曲线越缓慢，拐点右移。对相同波数，梯度系数η越大其相速度值越大；但随模态阶数的增加梯度变化对相速度影响逐渐减小。在电学短路边界条件下，一阶模态相速度趋于功能梯度压电层界面处的B－G波波速，二阶以上模态相速度趋于功能梯度压电层界面处剪切体波波速。

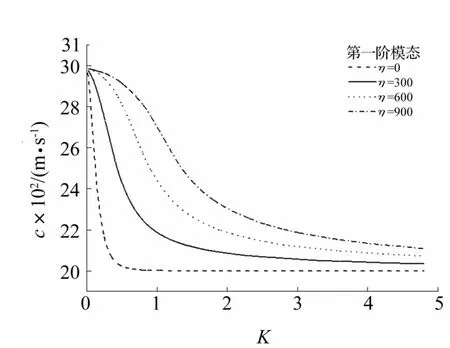
图2 电学短路η取不同数值时一阶模态频散曲线Fig.2 Dispersive curves of the first mode for selected values ofη

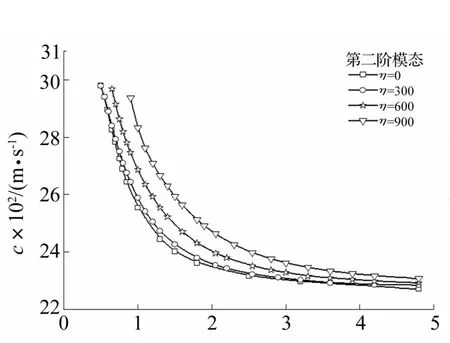
图3 电学短路η取不同数值时二阶模态频散曲线Fig.3 Dispersive curves of the second mode for selected values ofη

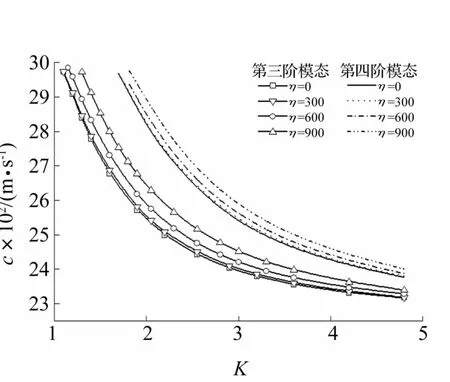
图4 电学短路η取不同数值时第三、四阶模态频散曲线Fig.4 Dispersive curves of the third and fourth modes for selected values ofη

为分析功能梯度压电层厚度对SH波传播频散曲线影响，给出PZT－5A／CoFe2O4层状半空间结构在电学短路边界条件下H取不同数值时SH波传播的一、二阶模态频散曲线见图5、图6。由图5看出，三条曲线基本重合，说明厚度变化对一阶模态影响较小，可忽略；无论H取何值，各阶模态相速度均起始于压磁半空间的剪切体波波速，并随无量纲波数增加一阶模态相速度趋于功能梯度压电层界面处的B－G波波速，二阶以上模态相速度趋于功能梯度压电层界面处剪切体波波速。由图6看出，对给定的波数二阶模态，覆盖层厚度H取值越大，相速度越小，尤其厚度取值从0.01 mm变化到0.03 mm时，相速度减小幅度较显著。

4.2 电学开路边界条件下频散特性分析

电学开路边界条件下功能梯度压电覆盖层中材料参数变化对前四阶模态频散曲线影响见图7～图10。由图7看出，无论η取何值，各阶模态相速度均起始于压磁半空间的剪切体波波速，且随无量纲波数的增加趋于功能梯度压电层界面处剪切体波波速，不同于电学短路边界条件下频散特性；梯度取较小值、一阶模态在小波数时，随波数增大相速度急剧减小，且较快减小至压电层界面处的剪切体波波速，随梯度取值增大相速度变化缓慢减小，与电学短路时变化相似。由图9、图10看出，无论H取何值，一阶模态相速度均起始于压磁半空间的剪切体波波速，随无量纲波数增加厚度取较大值时，相速度减小幅度较大，但最终趋于功能梯度压电层界面处的剪切体波波速，不同于电学短路边界条件下频散特性；二阶模态，对给定波数相速度随覆盖层厚度增大而减小，尤其厚度取值从0.01 mm变化至0.03 mm时，相速度减小幅度较显著。

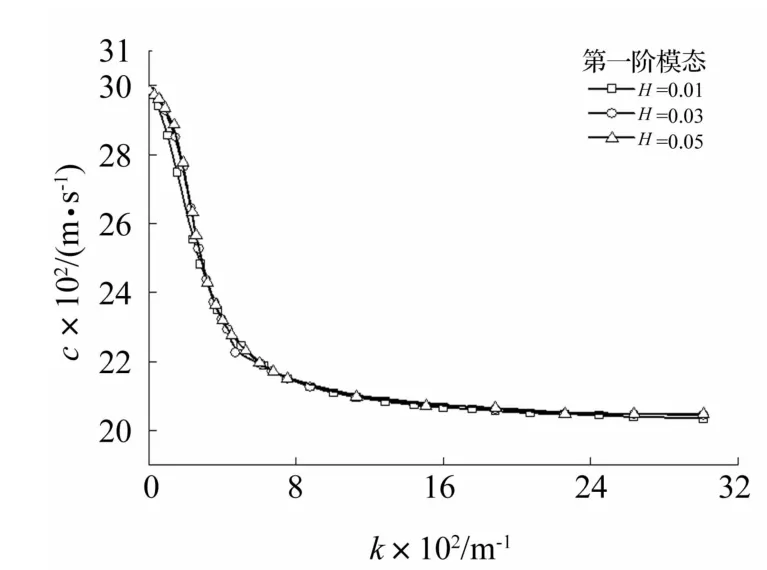
图5 电学短路H取不同数值时一阶模态频散曲线Fig.5 Dispersive curves of the first mode for selected values of H

图6 电学短路H取不同数值时二阶模态频散曲线Fig.6 Dispersive curves of the second mode for selected values of H

图7 电学开路η取不同数值时一阶模态频散曲线Fig.7 Dispersive curves of the first mode for selected values ofη

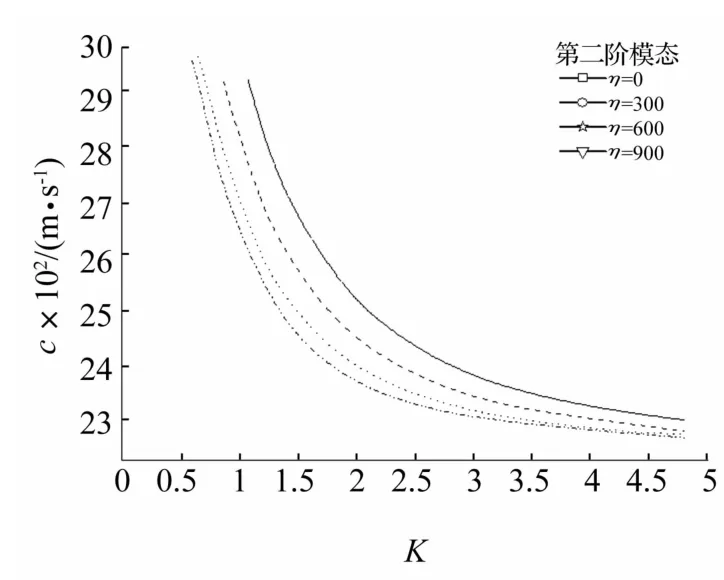
图8 电学开路η取不同数值时二阶模态频散曲线Fig.8 Dispersive curves of the second mode for selected values ofη

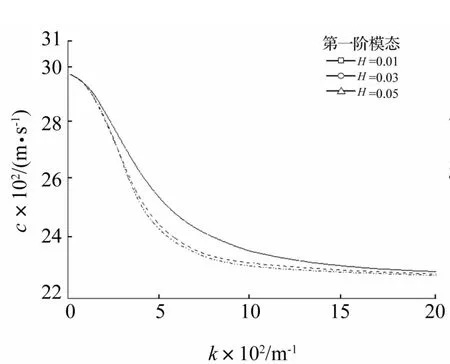
图9 电学开路H取不同数值时一阶模态频散曲线Fig.9 Dispersive curves of the first mode for selected values of H

图10 电学开路H取不同数值时二阶模态频散曲线Fig.10 Dispersive curves of the second mode for selected values of H

5 结 论

本文通过研究功能梯度压电层／均匀压磁半空间（PZT－5A／CoFe2O4）结构中SH波的传播特性，详细讨论功能梯度压电层梯度系数及厚度对SH波传播频散曲线影响，结论如下：

（1）相速度不仅随梯度系数增加而增大，亦会随覆盖层厚度增加而减小。

（2）电学短路条件时，梯度层厚度改变对一阶模态影响可忽略。

本文研究成果可为研制、设计高性能声波器件提供理论参考。

［1］赵军，艾兴，张建华.功能梯度材料的发展及展望［J］.材料导报，1997，11（4）：57－60.ZHAO Jun，AI Xing，ZHANG Jianhua.The development and prospects of functionally graded materials［J］.Materials Science，1997，11（4）：57－60.

［2］Liu J，Cao X S，Wang Z K.Love waves in a smart functionally graded piezoelectric composite structure［J］.Acta Mechinca，2009，208（1／2）：63－80.

［3］Qian Z H，Jin F，Lu T J，et al.Effect of initial stress on Love waves in a piezoelectric structure carrying a functionally graded material layer［J］.Ultrasonics，2010，50（1）：84－90.

［4］ Qian Zhenghua，Jin Feng，Lu Tianjian，et al.Transverse surface waves in a functionally graded piezoelectric substrate coated with a finitethickness metal waveguide layer［J］.Applied Physics Letters，2009，94（2）：023501.

［5］ Qian Zhenghua，Jin Feng，Wang Zikun，et al.Transverse surface waves on a piezoelectric material carrying a functionally graded layer of finite thickness［J］.International Journal of Engineering Science，2007，45（2／8）：455－466.

［6］Eskandari M，Shodja H M.Love waves propagation in functionally graded piezoelectric materials with quadratic variation［J］.Journal of Sound and Vibration，2008，313（1／2）：195－204.

［7］Du Jianke，Jin Xiaoying，Wang Ji，et al. Love wave propagation in functionally graded piezoelectric material layer［J］.Ultrasonics，2007，46（1）：13－22.

［8］Du Jianke，Chen Wuchao，Wang Ji，et al.Love waves in functionally graded magnetoelectroelastic material structures［C］.IEEEInternational Ultrasonics Symposium Proceedings，2008：1819－1822.

［9］Li Peng，Jin Feng，Qian Zhenghua.Propagation of the BleusteinGulyaev waves in a functionally graded transversely isotropic electromagnetoelastic halfspace［J］. European Journal of MechanicsA／Solids，2013，37：17－23.

［10］董小峰，禹建功，丁俊才.压电功能梯度材料中的SH表面波［J］.声学技术，2011，30（5）：387－390.DONG Xiaofeng，YU Jiangong，DING Juncai.SH surface wave in piezoelecelastic functionally graded materials［J］.Technical Acoustics，2011，30（5）：387－390.

［11］谢根全，申中原，胡邦南.电磁功能梯度材料层合板中表面波的弥散特性［J］.振动与冲击，2009，28（4）：98－102.XIE Genquan， SHEN Zhongyuan， HU Bangnan.Dispersion of surface wave in a functionally graded electromagnetoelastic layered plate［J］.Journal of Vibration and Shock，2009，28（4）：98－102.

［12］Wu Bin，Yu Jiangong，HE Cunfu.Wave propagation in nonhomogeneous magnetoelectroelastic plates［J］.Journal of Sound and Vibration，2008，317：250－264.

［13］Yu J G， Ma Q J， Su S. Wave propagation in nonhomogeneous magnetoelectroelastic hollow cylinders［J］.Ultrasonics，2008，48：664－677.

［14］栾桂冬，张金铎，王仁乾.压电换能器和换能器阵［M］.北京：北京大学出版社，2005：93－96.

［15］Srinivas S， Li J Y， Zhou Y C， et al. The effective magnetoelectroelastic moduli of matrixbased multiferroic composites［J］.J Appl phys，2006，99（4）：043905－1－043905－7.

［16］Liu Jinxi，Fang Daining，Wei Weiyi，et al.Love waves in layered piezoelectric／piezomagnetic structures［J］.Journal of Sound and Vibration，2008，315：146－156.